Matched-Filter

Autoren: Phillip Blunck, Marius Schaffer

"Unter Optimalfilter (engl. matched filter) versteht man in der Nachrichtentechnik ein Filter, welches das Signal-Rausch-Verhältnis (engl. signal to noise ratio, SNR) optimiert. In der Literatur findet man auch häufig die Bezeichnungen Korrelationsfilter, Signal-angepasstes Filter (SAF) oder nur angepasstes Filter. Das Optimalfilter dient zur optimalen Bestimmung des Vorhandenseins (Detektion) der Amplitude oder der Lage einer bekannten Signalform in Gegenwart von Störungen (Parameterschätzung)" ^[1].

Aufgaben

Analysieren Sie die Funktion des Matched-Filters im Ardumower Quellcode.
Setzen Sie das Matched-Filter in Simulink um.
Testen Sie die Funktion.
Dokumentieren Sie Ihre Ergebnisse wissenschaftlich.

Deadline für diese Teilaufgabe: 09.11.17

Herangehensweise

Machen Sie sich mit dem Quelltext des Ardumower Projektes vertraut.
1. Mit welcher Abtastrate wird der ADU betrieben?
2. Wie funktioniert das Matched-Filter?
Machen Sie sich anhand der Literatur unten mit der Theorie des Matched-Filters vertraut.
Machen Sie Aufzeichnungen mit dem Oszilloskop. Im Vergleich müssen hier die Eingangsgrößen für das Filter aufgezeichnet werden.-erledigt
Machen Sie Aufzeichnungen für unterschiedliche Abstände von Draht sowie außerhalb, innerhalb und auf dem Draht.-erledigt
Lesen Sie diese Aufzeichnungen sequenziell in Simulink ein.-erledigt
Wenden Sie das Matched-Filter darauf an, so dass der Wert 1 für innerhalb und -1 für außerhalb der Leiterschleife ausgegeben wird.-erledigt
Ersetzen Sie die offline Datenquelle durch die Echtzeitmessungen vom Arduino.-erledigt
Testen Sie das System, so dass auch für die Echtzeitmessungen der Wert 1 für innerhalb und -1 für außerhalb der Leiterschleife ausgegeben wird.-erledigt
Lässt sich aus der Signalstärke der Abstand zum Draht schätzen? -erledigt
Dokumentieren Sie Messaufbau, Durchführung und Ergebnis in diesem Artikel.

Theorie des Matched Filters

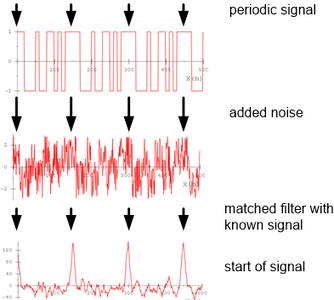
Das Ausgangssignal wird durch das Umgebungsrauschen so gestört, sodass das Signal nur noch sehr schlecht interpretiert werden kann. Aus diesem Grund sendet der Sender das ausgewählte digitale Signal, welches oben in der Abbildung 1 zu sehen ist. Diese Signal wird mit dem Umgebungsrauschen überlagert und muss nun gefiltert werden. Dies wird mit dem Matched-Filter gemacht. Nach Anwenden des Matched-Filter erhält man ein Signal, was entweder Pieks ins Positive oder Negative zur Folge hat. Anhand dieses Ergebnisses lässt sich einfach bestimmen, ob sich der ArduMower innerhalb oder außerhalb der Perimeterschleife befindet. Der Matched-Filter vergleicht das eingehende Signal mit einem Referenzsignal und korreliert es. Findet sich wie in der Abbildung 1 eine Korrelation wieder, erhält der Matched Filter das entsprechende Piek. Umso mehr Pieks entstehen, umso höher ist die vorherrschende Korrelation.

Versuchsaufbau/Auswertung mit Oszilloskop

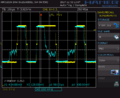
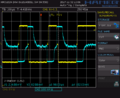
Als erste Simulation eines Matched-Filters wird mit einem Oszilloskop die empfangenen Signale innerhalb und außerhalb einer Perimeterschleife aufgenommen und aufgezeichnet. In den Abbildungen 1 bis 3 sind die verschiedenen Aufzeichnungen des Oszilloskops zu sehen. In gelb ist jeweils das Signal der Senderbox und in blau das empfangenen Signal der Empfängerspule zu sehen. Die aufgezeichneten Werte werden nun mit einen USB-Stick ausgelesen und im nächsten Kapitel mit Matlab/Simulink auf den Matched Filter angewendet.

Abb.1: Perimeterschleife Signal innerhalb der Schleife
Abb.2: Perimeterschleife Signal außerhalb der Schleife
Abb.3: Perimeterschleife Signal weit außerhalb der Schleife

Matched Filter Anwendung in Simulink

Mithilfe der aufgenommenen Werte des Oszilloskops ist es möglich mit dem Signal Generator Block in Matlab/Simulink die empfangenen und gesendeten Signale zu erzeugen und diese an den Matched Filter weiterzugeben. In der Abb. 4 sind das Sendersignal und die 3 verschiedenen empfangenen Signale der Empfängerspule mit dem Signalgenerator erzeugt worden. Anhand der Messwerte des Oszilloskops erzeugt der Signal Generator das passende Signal. Das Simulink Matched-Filter-Modell (Abb.5) besteht aus dem Signal Generator, dem Matched Filter und 3 verschiedenen Scopes. Der Matched-Filter erhält zwei inputs und gibt einen Output heraus. Im Eingang X erhält der Matched Filter das empfangene Signal der Spule und vergleicht dieses an dem Coeff Eingang zu bistimmten Sample Times mit dem Sendersignal. In den Abbildungen 6 bis 8 sind die verschiedenen Ergebnisse des Matched Filters aufgzeichnet.

Abb.4: Die erzeugten Signale im Signalgenerator
Abb.5: Siumlink Matched-Filter-Modell
Abb.6: Signalergebnis innerhalb der Schleife
Abb.7: Signalergebnis außerhalb der Schleife
Abb.8: Signalergebnis weit außerhalb der Schleife

Aufgrund der erhaltenen gefilterten Werte des Matched-Filters aus der Simulink Library ist eine eindeutige Zuordnung des Standortes in Bezug auf die Perimeterschleife nicht gewährleistet. Eine endeutige Zuweisung eines Wertes zum Zustand kann nicht getroffen werden. Außerdem kann anhand dieses Filter ebenfalls nicht der Abstand des Roboters zur Perimeterschleife detektiert werden. Als Lösung für dieses Probelem wird eine eigenständige S-Funcction mit dem vorhandenen Arduino C-Code umgesetzt. Diese Lösung wird im nächsten Kapitel erläutert.

Ergebnis der Umseztung in Matlab/Siumlink anhand einer S-Function

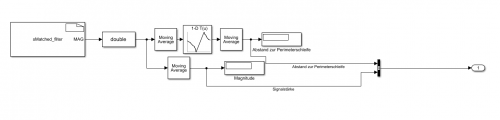
Mithilfe des S-Function Builder Blocks ist es möglich selbst einen Block mit den gewünschten Anforderungen zu erstellen. Dieser Block erhält von dem Pin A5 des Ardunios das empfangene Signal an der Empfängerspule und matched dieses Signal mit einem vorher festgelegten Referenzsignal und gibt ein Magnitude, d.h die Stärke des Signals, in Abhängigkeit von dem Abstand und dem Zustand in Bezug auf die Perimeterschleife aus. Die Magnitude Werte befinden sich im Intervall von ca. -1800 bis 1800. Ist der Wert negativ befindet sich die Spule außerhalb der Schleife und ist er positiv so befindet sie sich innerhalb der Schleife. Umso negativer das Signal ist, desto näher befindet sich die Spule an der Schelife und umso höher der positive Wert ist umso näher ist die Spule innerhalb der Schleife. Diese Magnitude Werte haben wir in Bezug auf den Abstand zur Perimterschleife in einer Look-Up Table festgehalten. Anhand dieser Werte können wir aufgrund der Stärke des Magnitude Wertes auf den Abstand zur Perimeterschleife schließen und diesen abschließend mit der passenden Polarität an die Bahnplanung weitergeben, die dadurch auf die Position des Roboters zurückschließen kann.

Quelltext

Der Quelltext des S-Function Matched-Filters

//Initilisierung
if (xD[0] != 1){
    # ifndef MATLAB_MEX_FILE
    Perimeter perimeter;
    ADCMan.init();
    perimeter.setPins(A5, A4);          
    perimeter.useDifferentialPerimeterSignal = true;
    ADCMan.calibrate();
    #endif
    xD[0]=1;
}
//main
if (xD[0]==1) {
    #ifndef MATLAB_MEX_FILE
          
    ADCMan.run();  
    MAG[0]=(int)perimeter.getMagnitude(0);
    # endif
}

Der Quelltext in dem S-Function Builder Block ruft ausschließlich Funktionen aus den angehängten Header Dateien des Ardumower Arduino Codes auf. Zum Verständnis der Funktion des ganzen Blocks müssen die einzelnen Header Dateien betrachtet werden. Der Quellcode istauf der Ardumower Seite frei erhältlich.

Quellen

http://www.grauonline.de/alexwww/ardumower/filter/filter.html

Literatur

Einzelnachweise

↑ Wikipedia-Artikel: Optimalfilter.

→ zurück zum Hauptartikel: Perimeterschleife

[1] Wikipedia-Artikel: Optimalfilter.

[1]