Seminaraufgabe SoSe 2021: Einspurmodell Gruppe F: Unterschied zwischen den Versionen

Version vom 10. Juli 2021, 14:42 Uhr

Autoren: Daniel Schwarz, Maik Kleinspohn

Einleitung

Entwicklungsprozess

Wie bereits in der Einleitung erwähnt wird nach dem V-Modell vorgegangen. Die wesentlichen Schritte zur Entwicklung des Linearen Einspurmodells werden im folgendem näher erläutert. Zuerst müssen die Rahmenbedingungen festgelegt werden. Dies erfolgt in der Anforderungsdefinition. Darauf aufbauend wird der funktionale Systementwurf erstellt, welcher den Rahmen zur Entwicklung vorgibt. Daraufhin werden mit dem technischen Systementwurf, benötigte Submodule und Ein- und Ausgänge der Module bestimmt. Im nächsten Schritt werden Komponenten der Submodule mithilfe der Komponentenspezifikation erstellt. Zuletzt zeigt dieses Kapitel das Gesamtmodell, welches in Simulink erzeugt wurde. Die Validierung des Modells und wie es anzuwenden ist, erfolgt in den darauffolgenden Hauptkapiteln.

Anforderungsdefinition

Um die Rahmenbedingungen festzulegen wurde mit einem Lastenheft gearbeitet. Das vollständige Lastenheft kann unter diesem Link eingesehen werden. Das Lastenheft wurde in fünf Kapitel unterteilt. Auszugsweise sind in Abbildung 1 und Abbildung 2 einige Anforderungen gezeigt. In Abbildung 1 sind Allgemeine Kriterien dargestellt. Dort wurde z.B. festgelegt das Arbeitsergebnisse im SVN hochgeladen werden oder welche groben Voraussetzungen erfüllt werden, siehe Anforderungs-ID 2 „Das lineare Fahrverhalten muss simuliert werden.“

Abb 1: Ausschnitt aus dem Lastenheft Kapitel 1 Allgemein

In Abbildung 2 ist zu erkennen, dass technische Grundbedingungen protokoliert wurden. Diese bestimmen z.B. die Paramater, siehe Anforderungs-ID 18 „Es müssen die Parameter Massenträgheit, Radstand, Schwerpunktabstand zur Vorderachse, Masse, Achssteifigkeit vorne und hinten berücksichtigt werden.“ oder auch die Darstellung, siehe Anforderungs-ID 23 „Die Diagramme müssen vertikal übereinander dargestellt werde.“

Insgesamt umfasst das Lastenheft 47 Anforderungen die in die Kapitel

Allgemein
Abgaben
Technisch
1. Eingänge
2. Ausgänge
3. Parameter
Software/Werkzeuge
Nachhaltigkeit/Dokumentation

untergliedert ist.

Dieses Dokument legt die Grundvoraussetzung für das Modell. Im Laufe der Entwicklung kam es vor, dass einzelne Anforderungen angepasst werden mussten oder die Liste erweitert/verkürzt wurde. Das Dokument im obigen Link entspricht dem Endstand des Lastenheft und kann zur Messung des Modells herangezogen werden.

Funktionaler Systementwurf

Der funktionale Systementwurf wird durch Herrn Prof. Göbel vorgegeben und kann Abbildung 3 entnommen werden. Zu sehen sind die drei Module Manöversteuerung, Modell und Auswertung. Im Modul Manöversteuerung werden in der späteren Programmierung die Fahrmanöver und Eingangsgrößen wie Längsgeschwindigkeit und Lenkwinkel in die Simulation geladen. Das Modul Modell umfasst alle Berechnungen die nötig sind für das Lineare Einspurmodell. Auf dieses wird in den folgenden Unterkapiteln noch näher eingegangen. Im letzten Modul Auswertung werden dann die errechneten Werte grafisch dargestellt. Die Darstellungen werden in späteren Unterkapiteln gezeigt. Der funktionale Systementwurf ist in Quelle 1^[1] enthalten.

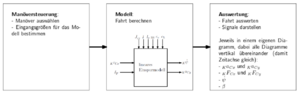
Technischer Systementwurf

Im technischen Systementwurf erfolgt die Umsetzung des funktionalen Systementwurf in Simulink. Für die drei Hauptmodule ist der Systementwurf in Abbildung 4 zusehen. Wie es im funktionalen Systementwurf bestimmt wurde, kommen aus dem Modul Manöversteuerung die Längsgeschwindigkeit und die Lenkwinkel für die Vorder- und Hinterachse (falls vorhanden, sonst ist dieser Wert = 0). Im Modul Modell werden diese Eingaben weiterverarbeitet und in die Ausgänge, die im Lastenheft bestimmt wurden berechnet. Zuletzt erfolgt die grafische Darstellung mit einem Scope im Modul Auswertung.

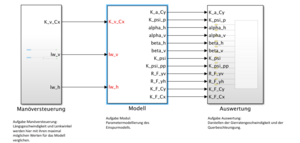
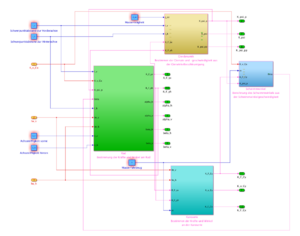
Abbildung 5 zeigt eine detailliertere Aufstellung der Subkomponenten im Modul Modell. Zur besseren Übersicht wurde das Modul in die Komponenten Gierdynamik, Rad, Schwimmwinkel und Karoserie unterteilt. Die Komponente Gierdynamik berechnet die Gierrate, -geschwindigkeit und -beschleunigung, die zum einen als Eingänge für andere Komponenten dienen, als auch im Modul Auswertung angezeigt werden sollen. Die Komponente Schwimmwinkel berechnet den Schwimmwinkel und dient damit als Eingang für weitere Komponenten. Die Komponente Rad kalkuliert die einzelnen Kräfte, die am Rad anliegen wie z.B. die Querkraft und die dafür nötigen Winkel wie z.B. Achs-Schräglaufwinkel und Achs-Schwimmwinkel. Die einzelnen Ausgänge aus dieser Subkomponente werden zur Anzeige im Modul Auswertung und als Eingänge für andere Komponenten benötigt. Im letzten Submodul Karoserie werden die insgesamt wirkenden Kräfte und Beschleunigungen in Quer- und Längsrichtung ermittelt. Auch diese Ausgänge werden sowohl als Eingänge für andere Komponenten als auch für die Darstellung im Modul Auswertung benötigt. Wie die Berechnungen der einzelnen Werte erfolgt wird im nächsten Kapitel Komponentenspezifikationen erläutert.

Der gesamte Technische Systementwurf kann in diesem Link eingesehen werden.

Komponentenspezifikation

Dieses Kapitel bezieht sich vollständig auf die Quelle 2^[2] die von Herrn Prof. Göbel zur Verfügung . gestellt wurde. Zunächst erfolgt die Berechnung der Achs-Schwimmwinkel vorne und hinten mit folgender Formel:

$\beta_v = \beta + \frac{l_v \cdot _K\dot{\psi}}{_Kv_{Cx}}$

$\beta_h = \beta - \frac{l_h \cdot _K\dot{\psi}}{_Kv_{Cx}}$

Gesamtmodell

Sonderzeichen setzen Sie einfach über [Alt]+ANSI Code z.B. [Alt]+0177: ±

Übersicht der ANSI-Code Sonderzeichen

Alternativ kann der Unicode eingegeben werden z.B. ❶ für ❶.

Modelltest

Komponententest

Integrationstest

Systemtest

Nutzen Sie zur Formatierung Beispiele, z. B. aus dem weltbekannten Wikipedia selbst (das ist die gleiche Syntax!) oder anderer Hilfeseiten wie z. B. ^[3].

Anwendung

Parameterdatei

MATLAB GUI

Anleitung und Beispiele zum Einbinden von Quelltext finden Sie hier: Quelltext_einbinden.

Fremdquellen sollten Sie auf jeden Fall zitieren. Internetquellen können Sie einfach verlinken. Literatur zitieren Sie bitte nach DIN ISO 690:2013-10.

Fazit

Was ist das Ergbnis? Das Ergebnis dieses Artikels ist eine Vorlage, mit der Nutzer des Wikis schnell und leicht eigene Artikel verwirklichen können. Diese Vorlage ist Bestandteil der Anleitungen aus den How-To's.

Was kann/muss noch verbessert werden?

Bauen Sie Bilder ein, am Besten mit darin gekennzeichneten Stellen, die Sie dann im Text erklären. Referenzieren Sie Bilder und Tabellen konsequent im Text. Zitieren Sie ggf. die Bildurheber.

Wenn Sie Bilder anzeigen möchten, ohne dass der Artikel links oder rechts weiter läuft, können Sie den Textfluss mit dem Befehl <br clear=all> stoppen (vgl. Abb. 2).

Alternativ können Sie das Bild in einer "wikitable" anzeigen lassen. Dadurch wird das Bild auch auf Bildschirmen mit einer anderen Auflösung in der richtigen Darstellungsart angezeigt (vgl. Abb. 3).

Abb 3: Beispiel wikitable

Hier geht es weiter mit dem Text.

Tabelle 1 zeigt ein schönes Beispiel.

Tabelle 1: Beispieltabelle
Spalte 1	Spalte 2	Spalte 3
blabla	sowieso	sowieso
test	sowieso	test1

Dieser Quelltext

<math> y = \int\limits_0^2 {\sin \frac{x}{2}dx}</math>

wird dann so dargestellt ${\displaystyle y = \int\limits_0^2 {\sin \frac{x}{2}dx} }$ .

Eine Übersicht über die Befehle findet sich z. B. hier: Gleichungen in math.

Literaturverzeichnis

↑ Göbel, M.: Systems Design Engineering Vorlesung & Seminar, FolienID 53ff.
↑ Göbel, M.: Fahrwerkmanagement Skript, Stand: 10.Juni.2020, Seite 12ff.
↑ Hilfeseite des Wikimedia-Projekts

[Seminaraufgabe-1] Göbel, M.: Systems Design Engineering Vorlesung & Seminar, FolienID 53ff.

[Einspurmodell-2] Göbel, M.: Fahrwerkmanagement Skript, Stand: 10.Juni.2020, Seite 12ff.

[3] Hilfeseite des Wikimedia-Projekts

[4] © Mirek Göbel - Eigenes Werk

[1]

[2]

[3]

[4]

@@ Zeile 65: / Zeile 65: @@
 === Komponentenspezifikation ===
-Dieses Kapitel bezieht sich vollständig auf die Quelle 2<ref name="Einspurmodell"> Göbel, M.: ''Fahrwerkmanagement Skript'',Stand: 10.Juni.2020, Seite 12ff.</ref> die von Herrn Prof. Göbel zur Verfügung . gestellt wurde. Alle folgenden Formeln können Seite 12ff entnommen werden.
+Dieses Kapitel bezieht sich vollständig auf die Quelle 2<ref name="Einspurmodell"> Göbel, M.: ''Fahrwerkmanagement Skript'', Stand: 10.Juni.2020, Seite 12ff.</ref> die von Herrn Prof. Göbel zur Verfügung . gestellt wurde.
 Zunächst erfolgt die Berechnung der Achs-Schwimmwinkel vorne und hinten mit folgender Formel:
+<math>\beta_v = \beta + \frac{l_v \cdot _K\dot{\psi}}{_Kv_{Cx}} </math>
-Dieser Quelltext
+<math>\beta_h = \beta - \frac{l_h \cdot _K\dot{\psi}}{_Kv_{Cx}} </math>
-<code type="latex">
-<nowiki><math></nowiki> y = \int\limits_0^2 {\sin \frac{x}{2}dx}<nowiki></math></nowiki>
-</code>
-wird dann so dargestellt
-<math>
-y = \int\limits_0^2 {\sin \frac{x}{2}dx}
-</math>.
-Eine Übersicht über die Befehle findet sich z. B. hier: [https://latex-kurs.de/fragen/Gleichungen_Basic.html Gleichungen in math].
@@ Zeile 170: / Zeile 162: @@
 |}
+Dieser Quelltext
+<code type="latex">
+<nowiki><math></nowiki> y = \int\limits_0^2 {\sin \frac{x}{2}dx}<nowiki></math></nowiki>
+</code>
+wird dann so dargestellt
+<math>
+y = \int\limits_0^2 {\sin \frac{x}{2}dx}
+</math>.
+Eine Übersicht über die Befehle findet sich z. B. hier: [https://latex-kurs.de/fragen/Gleichungen_Basic.html Gleichungen in math].
 == Literaturverzeichnis ==
 <references />