Autonome Längs- und Querregelung: Unterschied zwischen den Versionen
mit Artikel BSF zusammengeführt |
|||
| Zeile 4: | Zeile 4: | ||
==Einleitung und Ziel== | ==Einleitung und Ziel== | ||
Im Rahmen des SDE-Praktikums beinhaltet ein Arbeitsbereich die Bahnplanung und die Spurführung. Die Tätigkeit unterteilt sich in die Bereiche Bahnplanung und Autonome Längs- und Querregelung. Im Sommersemester 2014 wurde der Themenbereich von [[Benutzer:Daniel_Block|Daniel Block]] und [[Benutzer:Torben_Petersen|Torben Petersen]] bearbeitet. Die Dokumentation beruht auf der Vorarbeit von Tobias Teicher, siehe ''Anleitung und Dokumentation Carolo-Cup 2013 Studiengang "Mechatronik" Schwerpunkt "System Design Engineering"''. | |||
Das Thema Autonome Längs- und Querregelung beinhaltet die Aufgaben | Das Thema Autonome Längs- und Querregelung beinhaltet die Aufgaben | ||
*Analyse Istgeschwindigkeitssignal, | *Analyse Istgeschwindigkeitssignal, | ||
| Zeile 174: | Zeile 176: | ||
Die Bestimmung der Sollgröße ist im Artikel [[BSF - Bahn- und Spurführung|BSF - Bahn- und Spurführung]] beschrieben. Im Folgenden wird die Umsetzung des Reglers dargestellt.<br> | Die Bestimmung der Sollgröße ist im Artikel [[BSF - Bahn- und Spurführung|BSF - Bahn- und Spurführung]] beschrieben. Im Folgenden wird die Umsetzung des Reglers dargestellt.<br> | ||
Die Querregelung ist mit einem PID-Regler umgesetzt, der dem Regler der Längsregelung weitgehend entspricht. Die Regelparameter können ebenfalls in der Parameterdatei ''param_BSF.m'' über die Parameter ''PAR_BsfQuer_PAnteil_f64'', ''PAR_BsfQuer_IAnteil_f64'' und ''PAR_BsfQuer_DAnteil_f64'' eingestellt werden. Die Parametrisierung im Simulations-Modell kann erst nach der Parametrisierung des Einspurmodells erfolgen. Die Stellgröße für den Soll-Lenkwinkel wird durch eine Sättigungsfunktion auf den maximalen Lenkwinkel des Fahrzeugs begrenzt. Die Grenzen können ebenfalls in der Parameterdatei ''param_BSF.m'' als Parameter ''PAR_BsfQuer_max_Lw_f64'' und ''PAR_BsfQuer_min_Lw_f64'' festgelegt werden. | Die Querregelung ist mit einem PID-Regler umgesetzt, der dem Regler der Längsregelung weitgehend entspricht. Die Regelparameter können ebenfalls in der Parameterdatei ''param_BSF.m'' über die Parameter ''PAR_BsfQuer_PAnteil_f64'', ''PAR_BsfQuer_IAnteil_f64'' und ''PAR_BsfQuer_DAnteil_f64'' eingestellt werden. Die Parametrisierung im Simulations-Modell kann erst nach der Parametrisierung des Einspurmodells erfolgen. Die Stellgröße für den Soll-Lenkwinkel wird durch eine Sättigungsfunktion auf den maximalen Lenkwinkel des Fahrzeugs begrenzt. Die Grenzen können ebenfalls in der Parameterdatei ''param_BSF.m'' als Parameter ''PAR_BsfQuer_max_Lw_f64'' und ''PAR_BsfQuer_min_Lw_f64'' festgelegt werden. | ||
==Querführungskonzept== | |||
Die Querführung des Fahrzeuges wird in zwei Bereiche unterteilt. Der erste Aspekt beinhaltet die Bahnplanung, die im folgenden in ihrer theoretischen Grundlage und der Umsetzung in Simulink dargestellt wird. Die Querregelung ist im entsprechenden Artikel [[Autonome Längs- und Querregelung|Autonome Längs- und Querregelung]] beschrieben. <br> | |||
Als Grundlage für das Querführungskonzept dient die Sollbahn, die durch das Team ''OSE - Objekt- und Spurerkennung'' aufgrund der Analyse der zu fahrenden Strecke mit Hilfe eines Polynoms zweiten Gerades, das durch die Parameter ''a'', ''b'' und ''c'' eindeutig beschrieben ist, zur Verfügung gestellt wird. Da in dieser Anwendung aufgrund der Geometrie des Fahrzeugs ein Vergleich der Soll- und Ist-Bahn nicht sinnvoll ist, muss ein Punkt auf der Bahn in der Vorrausschauweite ''x'' prädiziert werden, an dem sich das Fahrzeug bei idealem Lenkwinkel und der aktuellen Geschwindigkeit befinden würde. Der ideale Lenkwinkel kann aber nicht bestimmt werden. Aus diesem Grund muss eine Abschätzung der Querabweichung von der einfachen Geradeausfahrt getroffen werden. Dabei wird der derzeitige Lenkwinkel als Referenz verwendet. Die Regeldifferenz des Querreglers bildet sich somit aus dem Punkt auf der Sollbahn und der prädizierten Positionsabschätzung. Die Vorrausschauweite ''x'' wird abhängig von der aktuellen Geschwindigkeit des Fahrzeugs berechnet. Der dazu verwendete Umrechnungsfaktor kann in der Parameterdatei ''param_BSF.m'' über den Parameter ''PAR_BSFQuer_GainVorausschauweite_f64'' eingestellt werden, der aktuelle Wert ist 0.2. | |||
===Sollbahnbestimmung=== | |||
Im Folgenden soll die Bestimmung des Punktes auf der Sollbahn beschrieben werden. Die Bahn wird als ein Polynom zweiten Gerades, einer Parabel, approximiert. Die allgemeine Formel lautet: <br> | |||
<math>y = a \cdot x^2 + bx + c \qquad(1)</math><br> | |||
Die Abbildung ''Schema der Sollbahn'' zeigt die Sollkurve im Fahrzeug-Koordinatensystem. Auch die Lage des Sollpunktes auf der Kurve ist dort qualitativ zu sehen. | |||
[[Datei:Schema der Sollbahn.PNG|500 px|center]] | |||
Die Bestimmung des prädizierten Punktes des Fahrzeuges auf der Ist-Bahn geschieht unter folgender Annahme: Ist der Lenkwinkel des Fahrzeuges gleich Null, existiert zwischen prädiziertem Ist-Punkt und der aktuellen Ausrichtung des Fahrzeuges keine Querabweichung. Fährt das Fahrzeug nicht exakt geradeaus, befindet es sich auf einer Kreisbahn, die bei stationär statischem Lenkwinkel konstant ist.<br> | |||
Der Radius dieser Kreisbahn lässt sich aus der stationären Gierrate und der Geschwindigkeit wie folgt bestimmen: <br> | |||
<math>r=\frac{v_0}{\dot\psi} \qquad(2)</math><br> | |||
Die Abbildung ''Schema der Istbahn'' zeigt die prädizierte Istbahn im Fahrzeug-Koordinatensystem und den Zusammenhang zwischen Querabweichung ''y'' und Vorrausschauweite ''x''. | |||
[[Datei:Schema der Istbahn.PNG|500 px|center]]<br> | |||
Zur Bestimmung der Querabweichung ''y'' wird der in der Skizze erkenntliche Zusammenhang zwischen dem Kreisradius ''r'' und der Vorausschauweite ''x'' verwendet. Mit dem ''Satz des Phythagoras'' kann ''a'' wie folgt bestimmt werden: <br> | |||
<math>r^2=x^2+a^2\Leftrightarrow a^2=r^2-x^2\Leftrightarrow a=\sqrt{r^2-x^2}\qquad(3)</math><br><br> | |||
Die Querabweichung ''y'' kann aus ''r'' und ''a'' bestimmt werden:<br> | |||
<math>y=r-a \qquad(4)</math> | |||
<br><br> | |||
Da die Vorrausschauweite ''x'' unabhängig vom derzeitigen Kurvenradius ''r'' bestimmt wird, kann der Ausdruck unter der Wurzel in '''(3)''' negativ sein. Weil diese Berechnung unzulässig wäre, wird vorbeugend das Ergebnis der Vorrausschauweitenberechnung mit einer Sättigungsfunktion begrenzt, die maximal 80 % des aktuellen Kurvenradius annimmt. Dieser Wert (80 % = 0.8) kann über den Parameter ''PAR_BSFQuer_VorrausschauBegrenzung_f64'' eingestellt werden.<br> | |||
Die Querabweichung der Sollbahn und die Querabweichung der Istbahn, jeweils bezogen auf die aktuelle Ausrichtung des Fahrzeuges, ergeben die Regeldifferenz für den Querregler. Aufgrund der Differenz zwischen Sollbahn und Istbahn bringt dieses Konzept eine bleibende Regelabweichung in der Kurve mit sich. Diese ist nur dann Null, wenn das Fahrzeug sich in der Geradeausfahrt befindet. | |||
===Status Quo=== | |||
In dem oben beschriebenen Konzept wird zur Bestimmung der Istbahn die Gierrate benötigt. Gemäß der Vorarbeit früherer Teams ist das Signal des Gyro-Sensors derzeit nicht verwendbar. Alternativ wurde daher ein neuer Ansatz zur Bestimmung der Regeldifferenz gewählt. Dabei wird angenommen, dass ohne Stellgrößenberechnung des Reglers das Fahrzeug auf einer Geraden fährt. Dadurch ergibt sich die Vereinfachung dahingehend, dass die prädizierte Istbahn des Fahrzeugs und die aktuelle Ausrichtung identisch sind, also dazwischen keine Querabweichung vorliegt. Als Regeldifferenz ergibt sich somit die Querabweichung der Sollbahn von der aktuellen Ausrichtung des Fahrzeugs. | |||
Die Querregelung wird im separaten Artikel [[Autonome Längs- und Querregelung|Autonome Längs- und Querregelung]] beschrieben. | |||
==Einspurmodell== | |||
Für die effikitve Nutzung des Offline-Modells in der Simulation ist eine Anpassung des Einspurmodells (ESM) an das Fahrzeug notwendig, damit das Modell der Realität so nah wie möglich kommt. Dazu müssen die einzelnen Parameter des Modells entsprechend bestimmt werden. Die aktuellen Werte sind in den Parameterdateien ''param_ESM_offline.m'' und ''param_CAR.m'' hinterlegt und werden somit vom Modell verwendet. | |||
===Größen des Einspurmodells=== | |||
Im Folgenden sollen die Parameter des Modells kurz vorgestellt werden. | |||
*Radstand des Fahrzeugs, wird im ESM mit ''l'' bezeichnet | |||
*Abstand des Schwerpunktes des Fahrzeuges von dem vordersten Punkt ''l<sub>v</sub>'' | |||
*Abstand des Schwerpunktes des Fahrzeuges von dem hintersten Punkt ''l<sub>h</sub>'' | |||
*Masse des Fahrzeugs ''m'' | |||
*Massenträgheitsmoment um die Z-Achse des fahrzeugfesten Koordinatensystems ''J'' | |||
*Steifigkeit der Vorderachse ''c<sub>v</sub>'' | |||
*Steifigkeit der Hinterachse ''c<sub>h</sub>'' | |||
===Bestimmung der Parameter=== | |||
Nun wird für die einzelnen Parameter die Bestimmung der jeweiligen Größen vorgestellt.<br> | |||
'''Radstand ''l'''''<br> | |||
Der Radstand lässt sich durch eine Messung mit einem Messschieber bestimmen. Es ist dabei der Abstand vom vorderen zum hinteren Achsenmittelpunkt zu messen. Für das Einspurmodell ist die Gesamtlänge, also inklusive der vorderen und hinteren Überhänge, nicht von Bedeutung.<br> | |||
'''Abstand des Schwerpunktes des Fahrzeuges von den äußeren Punkten ''l<sub>v</sub>'' und ''l<sub>h</sub>'''''<br> | |||
Zur Bestimmung der Abstände wird das Fahrzeug an den beiden Achsen mit zwei Waagen gewogen. Aus dem Verhältnis der bestimmten Maßen lässt sich die Lage des Schwerpunktes in Längsrichtung des Fahrzeugs bestimmen.<br> | |||
'''Masse des Fahrzeugs ''m'''''<br> | |||
Die Gesamtmasse ergibt sich aus der Summe der zwei zuvor bestimmten Teilmassen.<br> | |||
'''Massenträgheitsmoment um die Z-Achse ''J<sub>z</sub>'''''<br> | |||
Das Massenträgheitsmoment um die Z-Achse ''J<sub>z</sub>'' wird bestimmt unter der Annahme, dass das Fahrzeug geometrisch einem Quader ähnelt.<br> | |||
Für die Bestimmung der Steifigkeiten und die Feinjustierung des Modells wird das Fahrzeug, das die Regelstrecke darstellt, mit einer Sprungantwort für einen Sprung des Lenkwinkels analysiert. Dazu wird die Gierrate des Fahrzeugs während des Sprungsignals gemessen. Das ESM lässt sich anhand dieser Messdaten parametrisieren, indem das Übertragungsverhalten des Fahrzeugs den vom Modell errechneten Daten vergleichend gegenübergestellt wird. | |||
==Ausblick== | ==Ausblick== | ||
| Zeile 180: | Zeile 236: | ||
* Wenn Auslegung Querregler in Simulation erfolgreich, dann Feinjustierung am Fahrzeug | * Wenn Auslegung Querregler in Simulation erfolgreich, dann Feinjustierung am Fahrzeug | ||
* Regler-Verhalten im Übergabe-Moment nach Nutzung der Fernbedienung | * Regler-Verhalten im Übergabe-Moment nach Nutzung der Fernbedienung | ||
* Messung der Gierrate mit neuem Gierraten-Sensor | |||
* Auslegung des ESM durch Justierung der Größen ''J'', ''c<sub>v</sub>'' und ''c<sub>h</sub>'' | |||
* Konzept für Hindernisumfahrung | |||
==Einzelnachweise== | ==Einzelnachweise== | ||
| Zeile 185: | Zeile 244: | ||
Autor: [[Benutzer:Nils Brunnert|Nils Brunnert]] ([[Benutzer Diskussion:Nils Brunnert|Diskussion]]) 13:02, 6. Feb. 2014 (CET) | Autor: [[Benutzer:Nils Brunnert|Nils Brunnert]] ([[Benutzer Diskussion:Nils Brunnert|Diskussion]]) 13:02, 6. Feb. 2014 (CET) | ||
<br>''Überarbeitet:'' [[Benutzer:Daniel Block|Daniel Block]] und [[Benutzer:Torben Petersen|Torben Petersen]] | <br>''Überarbeitet:'' [[Benutzer:Daniel Block|Daniel Block]] und [[Benutzer:Torben Petersen|Torben Petersen]] im Sommersemester 2014 | ||
== Verbesserungsvorschläge zum Artikel == | == Verbesserungsvorschläge zum Artikel == | ||
Version vom 23. Oktober 2014, 14:59 Uhr
Einleitung und Ziel
Im Rahmen des SDE-Praktikums beinhaltet ein Arbeitsbereich die Bahnplanung und die Spurführung. Die Tätigkeit unterteilt sich in die Bereiche Bahnplanung und Autonome Längs- und Querregelung. Im Sommersemester 2014 wurde der Themenbereich von Daniel Block und Torben Petersen bearbeitet. Die Dokumentation beruht auf der Vorarbeit von Tobias Teicher, siehe Anleitung und Dokumentation Carolo-Cup 2013 Studiengang "Mechatronik" Schwerpunkt "System Design Engineering".
Das Thema Autonome Längs- und Querregelung beinhaltet die Aufgaben
- Analyse Istgeschwindigkeitssignal,
- Analyse Gierrate,
- Regelung längs und
- Regelung quer.
Das Ziel der Aufgabe ist die Auslegung der Längs- und Querregelung des Fahrzeugs.
Analyse Istgeschwindigkeit
Die Aufzeichnung der Istgeschwindigkeit war zunächst nicht möglich, weil die in ControlDesk eingestellte Sollgeschwindigkeit nicht umgesetzt wurde. Unabhängig davon welcher Wert mit dem Slider vorgegeben wurde, fuhr das Fahrzeug immer rückwärts.<br\> Zur Lösung des Problems wurde die manuelle Gas-Vorgabe analysiert. Der Wert des Sliders wird mit der Look-Up-Table (LUT) Look Up Gaspedal im Block AktRtiPwm-PWM4fach-Modul in die entsprechende PWM-Breite zur Ansteuerung der Motoren umgewandelt.<br\> Das PWM-Eingangssignal AktFernb_PwmBreiteGasfernb_f64 im Block SenFernb - Fernbedienung wurde ermittelt, um die Breite der PWM bei neutraler Stellung, bei der maximalen Geschwindigkeit in Vorwärts- und Rückwärts-Fahrt zu identifizieren. <br\>
Diese Werte wurden in die LUT Look Up Gaspedal im Block AktRtiPwm-PWM4fach-Modul eingetragen (siehe Abbildung Function Block Parameters: Look Up Gaspedal).
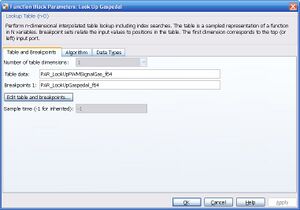
Hierzu wurde der Parameter PAR_LookUpPWMSignalGas_f64 gleich [0.0741 0.09144 0.1292] gesetzt. Der Parameter wird in der Datei param_SEN_offline.m definiert.<br\>
Nach dieser Einstellung kann über ControlDesk die Fahrtrichtung und die Geschwindigkeit vorgegeben werden.<br\>
Darstellung der Messung Istgeschwindigkeit (Rohwert)
Zur Aufzeichnung der Rohwerte der Istgeschwindigkeit wurden in einer Testfahrt verschiedene Fahrmanöver aufgezeichnet. Die Geschwindigkeit wurde mit dem Layout Geschwindigkeit in ControlDesk vorgegeben und das Fahrzeug wurde mit der Fernbedienung gelenkt. Abbildung Gasgeben zeigt die Kontrollinstrumente zur Vorgabe der Geschwindigkeit.

Das manuelle Gasgeben per Slider muss über die gleichnamige Checkbox aktiviert werden. Ist das manuelle Gasgeben aktiviert leuchtet die LED rechts neben der Checkbox grün. Die Geschwindigkeit kann jetzt über den Slider PAR_BsfLaengs_GasSollManuell_f64 eingestellt werden. Das Geschwindigkeitssignal SenVx_vx_unfilt_K_f64 wurde mit der Rekorder-Funktion von ControlDesk aufgezeichnet und unter Testfahrt_Istgeschw.mat gespeichert. Im Artikel Messungen aufnehmen ist die Vorgehensweise zum Aufnehmen von Messwerten erläutert.<br\>
Die nebenstehende Abbildung zeigt die aufgezeichneten Rohdaten der Istgeschwindigkeit.
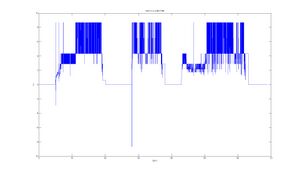
Nach Stillstand zu Beginn der Messfahrt wurde in 2s auf 4m/s beschleunigt und 4s mit konstanter Geschwindigkeit gefahren. Anschließend wurde noch einmal beschleunigt und nach einer 8s dauernden Fahrt mit einer konstanten Geschwindigkeit von 8m/s wurde das Fahrzeug angehalten. Im Anschluss wurde das Fahrzeug wieder beschleunigt und 9s mit der konstanten Geschwindigkeit 8m/s gefahren bis das Fahrzeug wieder gestoppt wurde. Der letzte Zyklus besteht aus einer Beschleunigung, einer 1s langen Fahrt mit 4m/s und anschließender Verringerung der Geschwindigkeit auf 2,5m/s. Nach 5s folgte eine weitere Beschleunigung auf 8m/s und nach einer 12s dauernden Fahrt mit dieser Geschwindigkeit wurde das Fahrzeug gestoppt und die Testfahrt nach 65s beendet.
Erstellung eines PT1-Filters
Die Erstellung eines PT1-Filters war nicht erforderlich, weil der vorhandene PT1-Filter PT_1_Eing_f des Moduls SenVx - Laengsgeschwindigkeit genutzt werden kann. Die Eingänge des Filters sind die ungefilterten Rohdaten der Istgeschwindigkeit (SenVx_vx_unfilt_K_f64) und die Filterfrequenz (PAR_SenGeschw_AnteilFrequenz). Der Ausgang ist die gefilterte Istgeschwindigkeit SenVx_vx_K_f64.
Auswahl einer Filterfrequenz
Zur Bestimmung der Filterfrequenz PAR_SenGeschw_AnteilFrequenz wurde die in Abbildung Testumgebung PT1-Filter Istgeschwindigkeit dargestellte Testumgebung Test_PT1_Laengsgeschw.mdl im Verzeichnis \trunk\Teams\BSF\Analyse Laengsgeschw\Test_PT1_Laengsgeschw erstellt.
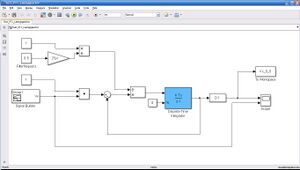
Die Eingänge der Testumgebung sind die während der Testfahrt aufgezeichneten Geschwindigkeitsdaten und die Filterfrequenz. Der Ausgang, die gefilterten Geschwindigkeitsdaten, werden in einem Scope angezeigt und im Workspace gespeichert. Das Einlesen der Geschwindigkeitsdaten wurde mit dem Signal Builder-Block realisiert. Hierzu wurden die aufgezeichneten Daten in einer xls-Datei gespeichert und als Signal dem Signal Builder-Block hinzugefügt. Die Spalte der Zeitdaten muss in der ersten Zeile Time enthalten und in der ersten Zeile der Spalte mit den Geschwindigkeitswerten muss der Name für die Werte in diesem Fall Vx stehen.<br\>
Die nebenstehende Abbildung zeigt das Dialogfenster Import File zum Hinzufügen des aufgezeichneten Signals zum Signal Builder.
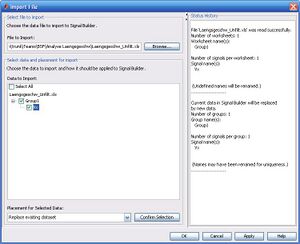
Im folgenden werden die Arbeitsschritte zum Hinzufügen eines aufgezeichneten Signals aufgeführt.
- Über die Funktion Import File werden die Daten der xls-Datei dem Signal Builder hinzugefügt.
- Über die Schaltfläche Browse wird die zu importierende xls-Datei ausgewählt.
- Im Feld Data to Import wird das Signal der xls-Datei ausgewählt.
- Im Drop-Down-Menü Placement for Selected Data Replace existing dataset auswählen.
- Alle Einstellungen mit einem Klick auf die Schaltfläche Confirm Selection bestätigen.
- Ein Klick auf OK lädt die Daten in den Signal Builder.
- Speichern und schließen des Signal Builders.
Die Istgeschwindigkeit wurde mit den Frequenzen
- 0,1Hz,
- 0,15Hz,
- 0,2Hz,
- 0,3Hz,
- 0,4Hz und
- 0,5Hz
gefiltert.<br\> Die gefilterten Signale wurden im Workspace gespeichert um sie vergleichen zu können. Die Messdaten und das Matlab-Skript zum Plot der Messungen sind im Verzeichnis \trunk\Teams\BSF\Analyse Laengsgeschw abgelegt.
In der Abbildung Geschwindigkeitssignal werden im oberen Diagramm die ungefilterten Rohdaten dargestellt. Das untere Diagramm zeigt die gefilterten Geschwindigkeiten für die oben aufgelisteten Frequenzen.<br\> Der Vergleich der gefilterten Signale hat ergeben, dass bei einer Filterfrequenz von 0,3Hz eine gute Rauschunterdrückung bei gleichzeitig geringem Delay erzielt wird. Wird eine höhere Frequenz gewählt, verringert sich die Zeitverzögerung, jedoch ist das Rasuchen auf dem gefilterten Signal zu hoch. Geringere Frequenzen weisen eine bessere Rauschunterdrückung auf, haben aber ein zu großes Delay.
Analyse Gierrate
Messung der Istgierrate (Rohwert)
Die Rohdaten der Istgierrate wurden während einer Testfahrt mit dem Fahrzeug aufgenommen. Es wurde zweimal eine Rechtskurve gefolgt von einer Linkskurve gefahren. Mit ControlDesk wurde eine konstante Geschwindigkeit vorgegeben und das Fahrzeug wurde mit der Fernbedienung gelenkt. Die Vorgabe der Geschwindigkeit wird in diesem Artikel unter Darstellung der Messung Istgeschwindigkeit (Rohwert) erklärt. Die Rohdaten der ungefilterten Istgierrate SenGier_psip_unfilt_K_f64 wurden mit dem ControlDesk-Rekorder aufgezeichnet und unter der Datei Analyse_Gierrate.mat gespeichert. Die Aufzeichnung von Messwerten mit ControlDesk ist im Artikel Messungen aufnehmen beschrieben.
Die aufgezeichneten Daten werden in der Abbildung Rohdaten Gierrate dargestellt.
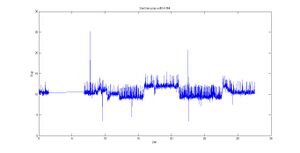
Nach einer 7s dauernden Geradeaus-Fahrt wurde 9s lang die erste Rechtskurve gefahren. Die folgende Linkskurve wurde 5s lang durchfahren. Die Dauer der zweiten Rechtskurve betrug 6s. Die zweite Linkskurve wurden ebenfalls 5s lang befahren.
Auswahl einer Filterfrequenz
Die Filterfrequenz des PT1-Filters für die Gierrate wird in dem Parameter PAR_SabGier_FilterF_K_f64 in der Datei param_SAB.m definiert. Zur Bestimmung der Filterfrequenz wurde der PT1-Filter der Gierrate in die Testumgebung Test_PT1_Gierrat.mdl eingebettet. Die Testumgebung ist im Verzeichnis \trunk\Teams\BSF\Analyse Gierrate abgelegt.<br\> Die aufgezeichneten Rohdaten der Istgierrate werden über den Signal Builder-Block in die Testumgebung geladen. Die zu testenden Filterfrequenzen werden über die Konstante Filterfrequenz eingestellt. Die gefiltere Gierrate wird im Workspace gespeichert und mit einem Scope ausgegeben.<br\> Die Rohdaten wurden mit den folgenden Frequenzen gefiltert:
Die gefilterten Gierraten sind unter \trunk\Teams\BSF\Analyse Gierrate abgelegt und werden mit dem Matlab-Skript Plot_Messfahrten_Gierrate.m zum Vergleichen dargestellt. In der Abbildung Gierrate werden im oberen Plot die Rohdaten der Istgierrate dargestellt. Das untere Diagramm zeigt die gefilterte Gierrate für die Frequenzen 0,3Hz, 0,4Hz, 0,5Hz, 0,7Hz und 0,8Hz. Dem Diagramm ist zu entnehmen, dass bei einer Filterfrequenz von 0,5Hz eine gute Rauschunterdrückung bei gleichzeitig geringer Zeitverzögerung realisiert wird. Diese Frequenz wurde deshalb als Filterfrequenz ausgewählt. Niedrigere Frequenzen haben ein höheres Delay und bei höheren Frequenzen ist die Rauschunterdrückung geringer.
Regelung längs
Die Längsregelung des Fahrzeugs erfordert eine exakte Bestimmung der Sollgeschwindigkeit. Aus diesem Grund wird in den folgenden zwei Abschnitten das Konzept zur Bestimmung der Sollgeschwindigkeit betrachtet.
Konzept zur Bestimmung der Sollgeschwindigkeit
<br\>Die Sollgeschwindigkeit des Fahrzeugs wird aus dem Krümmungsradius der Fahrbahn bestimmt. Die im Online-Modus von der Kamera erfasste Fahrbahn wird mit einer Parabel im Fahrzeug-Koordinatensystem modelliert. Diese ist bestimmt über die drei Koeffizienten a, b und c. Nach der allgemeinen Parabelgleichung ax²+bx+c beschreibt a die Krümmung der Kurve und wird im Block SenKam - Kamera in den Kameraparameter a geschrieben und als Signal SenKam_SpurA_f64 ausgegeben.<br\>
Im Online-Modell ist der Ausgang für Parameter A mit Ground verbunden, weil die Kameraauswertung auf Grund der fehlenden Kommunikation keine Daten an SenKam - Kamera überträgt.<br\>
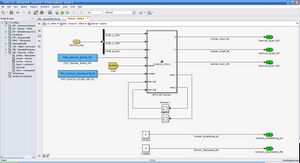
Im Offline-Modus wird der Kameraparameter a aus der Position und der Richtung des im Einspurmodell simulierten Fahrzeugs berechnet. Die Parameter ESM_x_I_f64 und ESM_y_I_f64 beschreiben die Position des Fahrzeugs. Die Richtung des Fahrzeugs steht im Parameter ESM_psi_f64. Der SenKam - Kamera-Block des Offline-Modells wird in Abbildung SenKam - Kamera (offline) dargestellt.
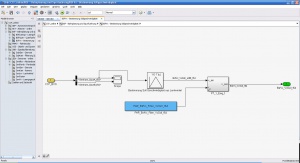
Die Sollgeschwindigkeit wird im Online-Modell und im Offline-Modell im rechts dargestellten Block BSFVx - Bestimmung Sollgeschwindigkeit unter BSF - Bahnplanung und Spurfuehrung bestimmt. Die Eingänge des Blocks sind die Kameraparameter SenKam_SpurA_f64 und SenKam_SpurB_f64. Beide können zu Diagnosezwecken in einem Scope angezeigt werden. SenKam_SpurA_f64 ist der Eingang der Look-Up-Table Bestimmung Soll Geschwindigkeit aus Lenkwinkel, in der die Sollgeschwindigkeit bestimmt wird. Die Parameter PAR_Famo_VxSollBSF_f64 und PAR_BSF_KameraAParameterVorgabe_f64 der LUT werden in der Datei param_BSF.m definiert. PAR_Famo_VxSollBSF_f64 enthält den Wert 5*[0.1 0.5 0.1] und PAR_BSF_KameraAParameterVorgabe_f64 den Wert [-0.5 0 0.5]. Daraus folgt, dass die maximale Geschwindigkeit bei keiner Krümmung 2,5m/s beträgt und die minimale Geschwindigkeit von 0,5m/s bei einem Krümmungsradius von 0,5 oder -0,5 vorgegeben wird. Das Ausgangssignal BsfVx_VxSoll_unfilt_f64 der LUT wird mit dem nachgeschalteten PT1-Filter PT_1_Eing_f geglättet. Die geglättete Sollgeschwindigkeit wird über den Ausgang BsfVx_VxSoll_f64 ausgegeben.<br\>
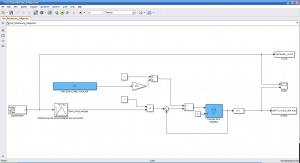
Zur Überprüfung des beschriebenen Konzepts wurde eine Testumgebung für den Block BSFVx - Bestimmung Sollgeschwindigkeit erstellt. Diese ist in der nebenstehenden Abbildung dargestellt. Der Krümmungsradius wird mit einem Signal Builder simuliert. Die Parameter der LUT und die Filterfrequenz PAR_BsfVx_Filter_VxSoll_f64 von 0,5Hz wurde aus der Datei param_BSF.m übernommen. Die Sollgeschwindigkeit und der simulierte Krümmungsradius werden zur Diagnose im Workspace gespeichert und mit einem Scope angezeigt. Der Krümmungsradius wird in der Datei Spurparam_A.mat und die Sollgeschwindigkeit unter BsfVx_VxSoll_f64.mat gespeichert.
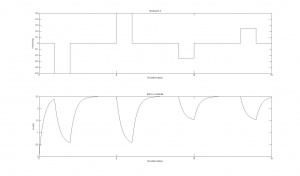
Das Diagramm in der Abbildung Ergebnis der Überprüfung des Sollgeschwindigkeitskonzepts zeigt das Ergebnis der Überprüfung.
Das obere Diagramm zeigt den simulierten Krümmungsradius und im unteren Diagramm ist die Sollgeschwindigkeit dargestellt.
Zu Beginn des Tests wird eine Rechtskurve mit einer maximalen Krümmung von -0,5 eine Sekunde lang simuliert. Drei Sekunden später wird eine ebenfalls eine Sekunde dauernde Linkskurve mit einem Krümmungsradius von 0,5 simuliert. Im unteren Diagramm ist für beide Krümmungen zu sehen, wie die Sollgeschwindigkeit bei den maximalen Krümmungen auf die minimale Geschwindigkeit 0,5m/s verringert wird. Hier ist der Grund für den PT1-Filter zu sehen. Wenn der Filter nicht verwendet würde, wäre der Verlauf der Sollgeschwindigkeit nicht geglättet, sonder sprunghaft wie der Verlauf des Krümmungsradius.
Im weiteren Verlauf der Simulation wird nach neun Sekunden eine schwächere Rechtskurve mit einer Krümmung von -0,25 für die Dauer von einer Sekunde simuliert. Nach weiteren 13 Sekunden wird eine Linkskurve mit dem Krümmungsradius 0,25 für eine Sekunde simuliert. Die Sollgeschwindigkeit wird bei diesen beiden Kurven auf einen Wert von 1,54m/s verringert. Wenn keine Kurve durchfahren wird, also wenn der Krümmungsradius 0 ist, nimmt die Sollgeschwindigkeit den maximale Wert von 2,5 m/s an.
Dieses Simulationsergebnis konnte mit einer Offline-Simulation im BSF-Modus bestätigt werden. Im Anschluss an die Offline-Simulation wurden die in der Abbildung Ergebnis der Offline-Simulation dargestellten Diagramme zur Analyse der Simulation ausgegeben.
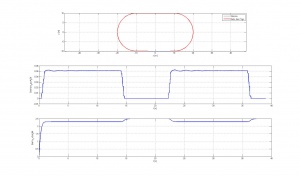
Das obere Diagramm zeigt die gefahrene Strecke auf dem Oval in rot. In der Mitte wird der Krümmungsradius der Farhbahn dargestellt. In der Zeit von 0s bis 15s wird die erste Linkskurve mit einer Krümmung von 0,05 durchfahren. Anschließend beträgt der Krümmungsradius auf der Geraden 0. Während der zweiten Linkskurve in der Zeit von 22s bis 36s beträgt die Krümmung ebenfalls 0,05. Nach der Durchfahrt der Kurve ist der Krümmungsradius wieder 0.<br\>
Im unteren Diagramm ist die Sollgeschwindigkeit über der Zeit aufgetragen. Dieses zeigt, dass während der Kurven die Sollgeschwindigkeit auf 2,3m/s verringert wird und auf den Geraden die maximale Sollgeschwindigkeit von 2,5m/s vorgegeben wird.<br\>
Die Überprüfung im offline-Modus hat ergeben, dass das vorhandene Konzept zur Bestimmung der Sollgeschwindigkeit verwendet werden kann. Eine Überprüfung im Online-Modus ist derzeit nicht möglich, da es keine Kommunikation zwischen der Kameraauswertung und dem Block SenKam - Kamera gibt.
Konzept zur Bestimmung der Sollgeschwindigkeit in Simulink umsetzen
Das aktuell in Simulink umgesetzte Konzept kann laut den Ergebnissen der Überprüfung verwendet werden.<br\>
Allerdings ist das Konzept im Online-Modus nach dem gleichen Verfahren wie im Offline-Modus zu überprüfen und die Filterfrequenz PAR_BsfVx_Filter_VxSoll_f64 im Block BSFVx - Bestimmung Sollgeschwindigkeit ist während der Testfahrten zu überprüfen und gegebenenfalls anzupassen.
Reglerentwurf
Für den Längsregler wurde ein separates Simulink-Modell angelegt, damit der Regler besser veranschaulicht werden kann. Der Regler besitzt einen P-, I- und D-Anteil.
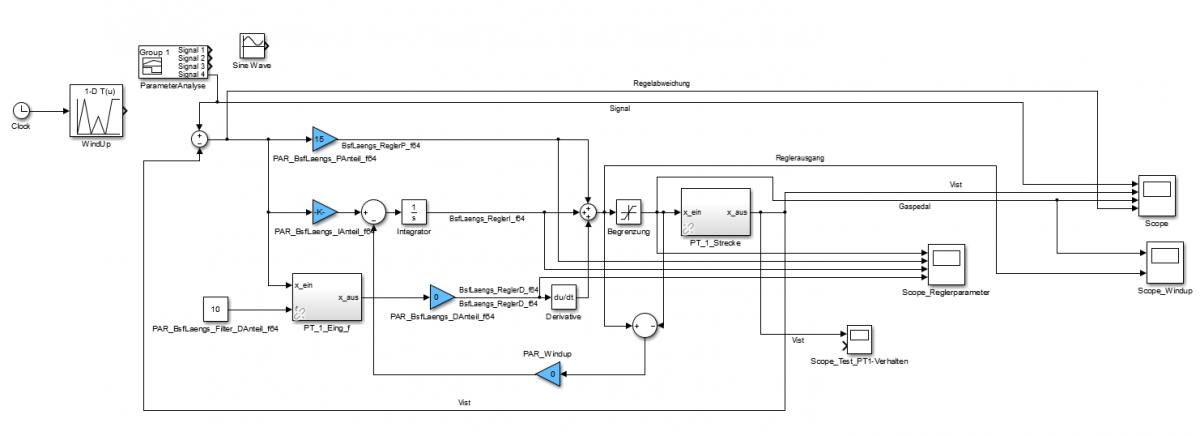
Für die Untersuchung der Regler-Parameter wurde ein Einheitssprung verwendet. Es wurden dabei folgende Feststellungen gemacht.
- Der P-Anteil ist für die Größe des "Einheitssprungs" verantwortlich. Mit größerem P-Anteil stellt sich außerdem ein zunehmendes Überschwingen ein.
- Mit dem I-Anteil wird die Stellgröße und der P-Anteil geglättet, jedoch ist für eine glatte Stellgröße ein sehr hoher I-Anteil erforderlich (größer als 150).
- Durch den D-Anteil kann der negative Ausschlag zu Beginn verringert werden. Mit größerem D-Anteil nimmt die Schwingung der Stellgröße zu.
Die Auswirkungen der Parameter wurden in einer Testreihe untersucht. Die Plots sind im SVN zu finden.
Wenn nur ein D-Anteil vorhanden ist, ist die Stellgröße nicht konstant. Im Test wurden für den D-Anteil die Werte [5 15 50] verwendet und der Wert 15 gewählt, weil die Totzeit am geringsten ist. Für größere Werte nimmt sie nicht weiter ab.
Im Test des I-Anteils wurde mit verschiedenen Werten experimentiert, eine konstante Stellgröße wurde erst ab einem Wert von 170 erreicht. Bei kleineren Werten konnte im Plot der Stellgröße noch eine Schwingung wahrgenommen werden.
Sobald der D-Anteil hinzukommt, geht die kostante Stellgröße verloren, jedoch wird der negative Ausschlag verringert. Allerdings kann auch mit einem sehr hohen I-Anteil von 500 die Stellgröße nicht geglättet werden.
Update Juni 2014
Nachdem eine Messung des Geschwindigkeitssignals am Fahrzeug vorgenommen und das System angepasst wurde, wurden folgende Parameter festgelegt:
- P-Anteil: 3
- I-Anteil: 1
- D-Anteil: 0
- Windup-Faktor: 10
Wind-Up

Die Stellgröße für das Gaspedal ist gemäß Anforderung auf das Intervall [-1 1] begrenzt. Aus diesem Grund ist im Simulink-Modell ein entsprechender Begrenzungsblock eingefügt, der den Wert des Regler-Ausgangs von -1 bis 1 begrenzt. Bei PI-Reglern mit einer derartigen Begrenzung tritt der Wind-Up-Effekt auf. Prof. Dr.-Ing. Frank Allgöwer beschreibt diesen folgendermaßen:
Bei einem Regler mit I-Anteil wird z.B. der so entstehende zusätzliche Regelfehler aufintegriert. Es folgt ein starkes Überschwingen, das bis zur Instabilität führen kann.[1]
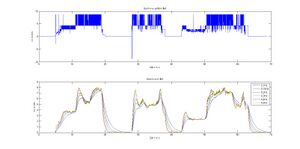
Im vorliegenden Modell wurde in der genannten separaten Simulations-Umgebung ein hoher Sprung als Sollgröße simuliert, vergleichlich Abbildung Windup-Problematik: Vergleich Soll- und Istgröße und Reglerparameter im Diagramm oben links. Das Aufintegrieren des I-Anteils kann dabei sehr gut beobachtet werden (Diagramm unten rechts in der Abbildung). Die Reaktion auf ein entsprechend niedrigeres Signal erfolgt dabei mit einer gewissen Totzeit, da der hohe I-Anteil erst abgebaut werden muss. Dieses ist im Plot der Ist-Geschwindigkeit (mitte links in der Abbildung) zu sehen.
Die Lösung dieser Problematik wird im Allgemeinen mit einer Anti-Windup-Strategie erreicht, die erstmalig akitv wird, wenn Sättigung auftritt, also wenn der Regler-Ausgang größer ist als die begrenzte Stellgröße.[2]
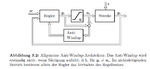

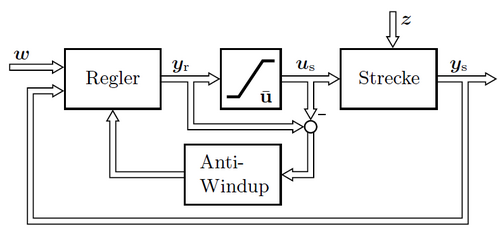
Wie in der Abbildung erkenntlich, wird dazu einfach der Wert am Ausgang des Reglers um den Wert nach der Begrenzung verringert. Die Abbildung Allgemeine Anti-Windup-Strategie zeigt auch den entsprechenden Beschreibungstext aus der Bildquelle. Ist die Differenz null, sind die Werte gleich groß und das Anti-Windup ist nicht aktiv. Stellt sich eine Differenz ein, wird über einen Verstärkerbaustein der Parameter für den I-Anteil um den entsprechenden Wert verringert. Als Faktor wurde der Wert „eins“ gewählt. Für das oben genannte Simulations-Beispiel konnte der Effekt der Anti-Windup-Strategie nachgewiesen werden. Es ist dabei besonders die geringere Totzeit im Plot der Ist-Geschwindigkeit und die schnelle Abnahme des I-Anteils zu beobachten.
Regelung quer
Die Bestimmung der Sollgröße ist im Artikel BSF - Bahn- und Spurführung beschrieben. Im Folgenden wird die Umsetzung des Reglers dargestellt.
Die Querregelung ist mit einem PID-Regler umgesetzt, der dem Regler der Längsregelung weitgehend entspricht. Die Regelparameter können ebenfalls in der Parameterdatei param_BSF.m über die Parameter PAR_BsfQuer_PAnteil_f64, PAR_BsfQuer_IAnteil_f64 und PAR_BsfQuer_DAnteil_f64 eingestellt werden. Die Parametrisierung im Simulations-Modell kann erst nach der Parametrisierung des Einspurmodells erfolgen. Die Stellgröße für den Soll-Lenkwinkel wird durch eine Sättigungsfunktion auf den maximalen Lenkwinkel des Fahrzeugs begrenzt. Die Grenzen können ebenfalls in der Parameterdatei param_BSF.m als Parameter PAR_BsfQuer_max_Lw_f64 und PAR_BsfQuer_min_Lw_f64 festgelegt werden.
Querführungskonzept
Die Querführung des Fahrzeuges wird in zwei Bereiche unterteilt. Der erste Aspekt beinhaltet die Bahnplanung, die im folgenden in ihrer theoretischen Grundlage und der Umsetzung in Simulink dargestellt wird. Die Querregelung ist im entsprechenden Artikel Autonome Längs- und Querregelung beschrieben.
Als Grundlage für das Querführungskonzept dient die Sollbahn, die durch das Team OSE - Objekt- und Spurerkennung aufgrund der Analyse der zu fahrenden Strecke mit Hilfe eines Polynoms zweiten Gerades, das durch die Parameter a, b und c eindeutig beschrieben ist, zur Verfügung gestellt wird. Da in dieser Anwendung aufgrund der Geometrie des Fahrzeugs ein Vergleich der Soll- und Ist-Bahn nicht sinnvoll ist, muss ein Punkt auf der Bahn in der Vorrausschauweite x prädiziert werden, an dem sich das Fahrzeug bei idealem Lenkwinkel und der aktuellen Geschwindigkeit befinden würde. Der ideale Lenkwinkel kann aber nicht bestimmt werden. Aus diesem Grund muss eine Abschätzung der Querabweichung von der einfachen Geradeausfahrt getroffen werden. Dabei wird der derzeitige Lenkwinkel als Referenz verwendet. Die Regeldifferenz des Querreglers bildet sich somit aus dem Punkt auf der Sollbahn und der prädizierten Positionsabschätzung. Die Vorrausschauweite x wird abhängig von der aktuellen Geschwindigkeit des Fahrzeugs berechnet. Der dazu verwendete Umrechnungsfaktor kann in der Parameterdatei param_BSF.m über den Parameter PAR_BSFQuer_GainVorausschauweite_f64 eingestellt werden, der aktuelle Wert ist 0.2.
Sollbahnbestimmung
Im Folgenden soll die Bestimmung des Punktes auf der Sollbahn beschrieben werden. Die Bahn wird als ein Polynom zweiten Gerades, einer Parabel, approximiert. Die allgemeine Formel lautet:
Die Abbildung Schema der Sollbahn zeigt die Sollkurve im Fahrzeug-Koordinatensystem. Auch die Lage des Sollpunktes auf der Kurve ist dort qualitativ zu sehen.
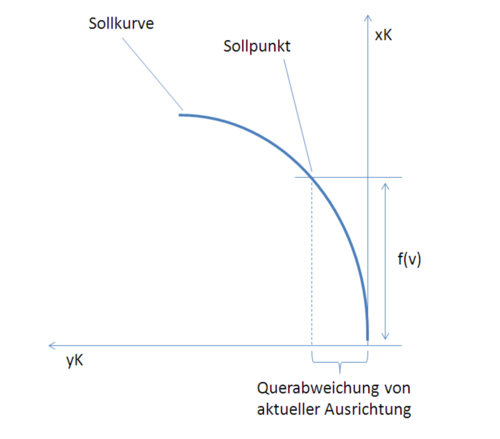
Die Bestimmung des prädizierten Punktes des Fahrzeuges auf der Ist-Bahn geschieht unter folgender Annahme: Ist der Lenkwinkel des Fahrzeuges gleich Null, existiert zwischen prädiziertem Ist-Punkt und der aktuellen Ausrichtung des Fahrzeuges keine Querabweichung. Fährt das Fahrzeug nicht exakt geradeaus, befindet es sich auf einer Kreisbahn, die bei stationär statischem Lenkwinkel konstant ist.
Der Radius dieser Kreisbahn lässt sich aus der stationären Gierrate und der Geschwindigkeit wie folgt bestimmen:
Die Abbildung Schema der Istbahn zeigt die prädizierte Istbahn im Fahrzeug-Koordinatensystem und den Zusammenhang zwischen Querabweichung y und Vorrausschauweite x.
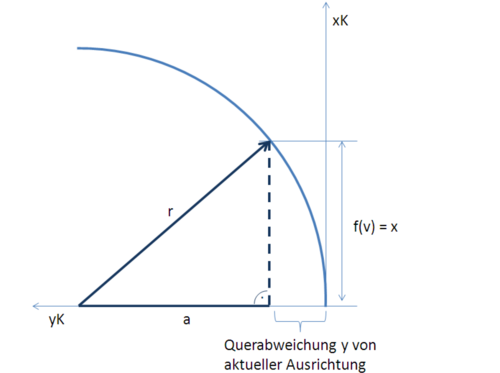
Zur Bestimmung der Querabweichung y wird der in der Skizze erkenntliche Zusammenhang zwischen dem Kreisradius r und der Vorausschauweite x verwendet. Mit dem Satz des Phythagoras kann a wie folgt bestimmt werden:
Die Querabweichung y kann aus r und a bestimmt werden:
Da die Vorrausschauweite x unabhängig vom derzeitigen Kurvenradius r bestimmt wird, kann der Ausdruck unter der Wurzel in (3) negativ sein. Weil diese Berechnung unzulässig wäre, wird vorbeugend das Ergebnis der Vorrausschauweitenberechnung mit einer Sättigungsfunktion begrenzt, die maximal 80 % des aktuellen Kurvenradius annimmt. Dieser Wert (80 % = 0.8) kann über den Parameter PAR_BSFQuer_VorrausschauBegrenzung_f64 eingestellt werden.
Die Querabweichung der Sollbahn und die Querabweichung der Istbahn, jeweils bezogen auf die aktuelle Ausrichtung des Fahrzeuges, ergeben die Regeldifferenz für den Querregler. Aufgrund der Differenz zwischen Sollbahn und Istbahn bringt dieses Konzept eine bleibende Regelabweichung in der Kurve mit sich. Diese ist nur dann Null, wenn das Fahrzeug sich in der Geradeausfahrt befindet.
Status Quo
In dem oben beschriebenen Konzept wird zur Bestimmung der Istbahn die Gierrate benötigt. Gemäß der Vorarbeit früherer Teams ist das Signal des Gyro-Sensors derzeit nicht verwendbar. Alternativ wurde daher ein neuer Ansatz zur Bestimmung der Regeldifferenz gewählt. Dabei wird angenommen, dass ohne Stellgrößenberechnung des Reglers das Fahrzeug auf einer Geraden fährt. Dadurch ergibt sich die Vereinfachung dahingehend, dass die prädizierte Istbahn des Fahrzeugs und die aktuelle Ausrichtung identisch sind, also dazwischen keine Querabweichung vorliegt. Als Regeldifferenz ergibt sich somit die Querabweichung der Sollbahn von der aktuellen Ausrichtung des Fahrzeugs.
Die Querregelung wird im separaten Artikel Autonome Längs- und Querregelung beschrieben.
Einspurmodell
Für die effikitve Nutzung des Offline-Modells in der Simulation ist eine Anpassung des Einspurmodells (ESM) an das Fahrzeug notwendig, damit das Modell der Realität so nah wie möglich kommt. Dazu müssen die einzelnen Parameter des Modells entsprechend bestimmt werden. Die aktuellen Werte sind in den Parameterdateien param_ESM_offline.m und param_CAR.m hinterlegt und werden somit vom Modell verwendet.
Größen des Einspurmodells
Im Folgenden sollen die Parameter des Modells kurz vorgestellt werden.
- Radstand des Fahrzeugs, wird im ESM mit l bezeichnet
- Abstand des Schwerpunktes des Fahrzeuges von dem vordersten Punkt lv
- Abstand des Schwerpunktes des Fahrzeuges von dem hintersten Punkt lh
- Masse des Fahrzeugs m
- Massenträgheitsmoment um die Z-Achse des fahrzeugfesten Koordinatensystems J
- Steifigkeit der Vorderachse cv
- Steifigkeit der Hinterachse ch
Bestimmung der Parameter
Nun wird für die einzelnen Parameter die Bestimmung der jeweiligen Größen vorgestellt.
Radstand l
Der Radstand lässt sich durch eine Messung mit einem Messschieber bestimmen. Es ist dabei der Abstand vom vorderen zum hinteren Achsenmittelpunkt zu messen. Für das Einspurmodell ist die Gesamtlänge, also inklusive der vorderen und hinteren Überhänge, nicht von Bedeutung.
Abstand des Schwerpunktes des Fahrzeuges von den äußeren Punkten lv und lh
Zur Bestimmung der Abstände wird das Fahrzeug an den beiden Achsen mit zwei Waagen gewogen. Aus dem Verhältnis der bestimmten Maßen lässt sich die Lage des Schwerpunktes in Längsrichtung des Fahrzeugs bestimmen.
Masse des Fahrzeugs m
Die Gesamtmasse ergibt sich aus der Summe der zwei zuvor bestimmten Teilmassen.
Massenträgheitsmoment um die Z-Achse Jz
Das Massenträgheitsmoment um die Z-Achse Jz wird bestimmt unter der Annahme, dass das Fahrzeug geometrisch einem Quader ähnelt.
Für die Bestimmung der Steifigkeiten und die Feinjustierung des Modells wird das Fahrzeug, das die Regelstrecke darstellt, mit einer Sprungantwort für einen Sprung des Lenkwinkels analysiert. Dazu wird die Gierrate des Fahrzeugs während des Sprungsignals gemessen. Das ESM lässt sich anhand dieser Messdaten parametrisieren, indem das Übertragungsverhalten des Fahrzeugs den vom Modell errechneten Daten vergleichend gegenübergestellt wird.
Ausblick
- Feinjustierung der Parameter der Längsregelung am Fahrzeug
- Nach der Parametrisierung des Einspurmodells Querregler im Simulations-Modell auslegen
- Wenn Auslegung Querregler in Simulation erfolgreich, dann Feinjustierung am Fahrzeug
- Regler-Verhalten im Übergabe-Moment nach Nutzung der Fernbedienung
- Messung der Gierrate mit neuem Gierraten-Sensor
- Auslegung des ESM durch Justierung der Größen J, cv und ch
- Konzept für Hindernisumfahrung
Einzelnachweise
- ↑ Allgöwer, Prof. Dr.-Ing. Frank: Vorlesung Regelungstechnik II. Institut für Systemtheorie technischer Prozesse, Universität Stuttgart. S. 1. (Link) (Abruf: 14.05.2014)
- ↑ vgl. Ortseifen, Andreas: Entwurf von modellbasierten Anti-Windup-Methoden für Systeme mit Stellbegrenzungen. S. 28. (Link) (Abruf: 14.05.2014)
Autor: Nils Brunnert (Diskussion) 13:02, 6. Feb. 2014 (CET)
Überarbeitet: Daniel Block und Torben Petersen im Sommersemester 2014
Verbesserungsvorschläge zum Artikel
--Ulrich Schneider (Diskussion) 13:38, 4. Feb. 2014 (CET)
- Autorenseite und Link zum Autor fehlt
--Prof. Dr. Mirek Göbel (Diskussion) 13:48, 8. Aug. 2014 (CEST)
- Führen Sie diesen Artikel mit dem Artikel BSF - ..." zusammen!
- Originaldateien zu den Bildern mit ablegen
- Abbildung der Regelstrecken als PT1 fehlt
- Zuviel Fließtext >> mehr Aufzählungen, Formeln etc., Reduktion aufs Wesentliche!
→ zurück zum Hauptartikel: Praktikum SDE
