Seminaraufgabe SoSe 2021: Einspurmodell Gruppe F: Unterschied zwischen den Versionen
| (89 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
[[Kategorie: | [[Kategorie:BSE/SDE-ESM]] | ||
→ zurück zum Hauptartikel: [["Systems Design Engineering" - Seminaraufgabe SoSe 2021: Einspurmodell“]] | |||
'''Autoren:''' [[Benutzer:Daniel_Schwarz|Daniel Schwarz]], [[Benutzer:Maik_Kleinspohn| Maik Kleinspohn]] | '''Autoren:''' [[Benutzer:Daniel_Schwarz|Daniel Schwarz]], [[Benutzer:Maik_Kleinspohn| Maik Kleinspohn]] | ||
<!-- Dies hier wird nicht angezeigt --> | <!-- Dies hier wird nicht angezeigt --> | ||
| Zeile 7: | Zeile 10: | ||
== Einleitung == | == Einleitung == | ||
Teil des | Teil des Moduls Systems Design Engineering im Studiengang Business and Systems Engineering ist die Seminaraufgabe, mit Themenschwerpunkt der Modellierung des linearen Einspurmodells. Das Modell soll meilensteinweise nach dem Vorgehen des V-Modells konzipiert, programmiert und getestet werden. Das Skript <ref name="Seminaraufgabe"> Göbel, M.: ''Systems Design Engineering Vorlesung & Seminar''.</ref> gibt eine Übersicht der genauen Aufgabenstellung, wie auch die Rahmenbedingung der Seminaraufgabe. | ||
== Entwicklungsprozess == | == Entwicklungsprozess == | ||
Wie bereits in der Einleitung erwähnt wird nach dem V-Modell vorgegangen. Die wesentlichen Schritte zur Entwicklung des | Wie bereits in der Einleitung erwähnt wird nach dem V-Modell vorgegangen. Die wesentlichen Schritte zur Entwicklung des linearen Einspurmodells werden im folgendem näher erläutert. Zuerst müssen die Rahmenbedingungen festgelegt werden. Dies erfolgt in der Anforderungsdefinition. Darauf aufbauend wird der funktionale Systementwurf erstellt, welcher den Rahmen zur Entwicklung vorgibt. Daraufhin werden mit dem technischen Systementwurf, benötigte Submodule und Ein- und Ausgänge der Module bestimmt. Im nächsten Schritt werden Komponenten der Submodule mithilfe der Komponentenspezifikation erstellt. Zuletzt zeigt dieses Kapitel das Gesamtmodell, welches in MATLAB Simulink erzeugt wurde. Die Validierung des Modells und wie es anzuwenden ist, erfolgt in den darauffolgenden Hauptkapiteln. | ||
=== Anforderungsdefinition === | === Anforderungsdefinition === | ||
Um die Rahmenbedingungen festzulegen wird mit einem Lastenheft gearbeitet. Das vollständige Lastenheft kann unter diesem [https://svn.hshl.de/svn/BSE_SystemsDesignEng/trunk/Projekte/ESM_SS2021/Gruppen/Gruppe%20F/01_Anforderungsdefinition/ Link] eingesehen werden. Das Lastenheft wird in fünf Kapitel unterteilt. | Um die Rahmenbedingungen festzulegen wird mit einem Lastenheft gearbeitet. Das vollständige Lastenheft kann unter diesem [https://svn.hshl.de/svn/BSE_SystemsDesignEng/trunk/Projekte/ESM_SS2021/Gruppen/Gruppe%20F/01_Anforderungsdefinition/ Link] eingesehen werden. Das Lastenheft wird in fünf Kapitel unterteilt. In Abbildung 1 sind allgemeine Kriterien aus dem Lastenheft dargestellt. Dort wird z.B. festgelegt, dass Arbeitsergebnisse im SVN hochgeladen werden. | ||
[[Datei:Ausschnitt_1_Lastenheft.PNG|links|mini|Abb 1: Ausschnitt aus dem Lastenheft Kapitel 1 Allgemein]] | [[Datei:Ausschnitt_1_Lastenheft.PNG|links|mini|Abb 1: Ausschnitt aus dem Lastenheft Kapitel 1 Allgemein]] | ||
| Zeile 27: | Zeile 29: | ||
Insgesamt umfasst das Lastenheft 47 Anforderungen die in die Kapitel | Insgesamt umfasst das Lastenheft 47 Anforderungen die in die Kapitel | ||
# Allgemein | |||
# Abgaben | #Allgemein | ||
# Technisch | #Abgaben | ||
## Eingänge | #Technisch | ||
## Ausgänge | ##Eingänge | ||
## Parameter | ##Ausgänge | ||
# Software/Werkzeuge | ##Parameter | ||
# Nachhaltigkeit/Dokumentation | #Software/Werkzeuge | ||
#Nachhaltigkeit/Dokumentation | |||
untergliedert sind. | untergliedert sind. | ||
Dieses Dokument legt die Grundvoraussetzung für das Modell. Im Laufe der Entwicklung kann es vorkommen, dass einzelne Anforderungen angepasst | Dieses Dokument legt die Grundvoraussetzung für das Modell. Im Laufe der Entwicklung kann es vorkommen, dass einzelne Anforderungen angepasst oder die Liste erweitert/verkürzt werden muss. Das Dokument im obigen Link entspricht dem Endstand des Lastenheft und kann zur Messung des Modells herangezogen werden. | ||
=== Funktionaler Systementwurf === | === Funktionaler Systementwurf === | ||
Der funktionale Systementwurf wird durch Herrn Prof. Göbel vorgegeben und kann Abbildung 3 entnommen werden. Zu sehen sind die drei Module Manöversteuerung, Modell und Auswertung. Im Modul Manöversteuerung werden in der späteren Programmierung die Fahrmanöver und Eingangsgrößen wie Längsgeschwindigkeit und Lenkwinkel in die Simulation geladen. Das Modul Modell umfasst alle Berechnungen die für das | Der funktionale Systementwurf wird durch Herrn Prof. Göbel vorgegeben und kann Abbildung 3 entnommen werden. Zu sehen sind die drei Module Manöversteuerung, Modell und Auswertung. Im Modul Manöversteuerung werden in der späteren Programmierung die Fahrmanöver und Eingangsgrößen wie Längsgeschwindigkeit und Lenkwinkel in die Simulation geladen. Das Modul Modell umfasst alle Berechnungen, die für das lineare Einspurmodell nötig sind. Auf dieses wird in den folgenden Unterkapiteln noch näher eingegangen. Im letzten Modul Auswertung werden dann die errechneten Werte grafisch dargestellt. Die Darstellungen werden in späteren Unterkapiteln gezeigt. Der funktionale Systementwurf ist in Quelle <ref name="Seminaraufgabe"> Göbel, M.: ''Systems Design Engineering Vorlesung & Seminar''.</ref> enthalten. | ||
[[Datei:Funktionaler_Systementwurf_Gruppe_F.PNG|links|mini|Abb 3: Funktionaler Systementwurf für das Lineare Einspurmodell]] | [[Datei:Funktionaler_Systementwurf_Gruppe_F.PNG|links|mini|Abb 3: Funktionaler Systementwurf für das Lineare Einspurmodell]] | ||
| Zeile 53: | Zeile 57: | ||
<br clear=all> | <br clear=all> | ||
Abbildung 5 zeigt eine detailliertere Aufstellung der Subkomponenten im Modul Modell. Zur besseren Übersicht wird das Modul in die Komponenten Gierdynamik, Rad, Schwimmwinkel und Karosserie unterteilt. Die Komponente Gierdynamik berechnet die Gierrate, -geschwindigkeit und -beschleunigung, die zum einen als Eingänge für andere Komponenten | Abbildung 5 zeigt eine detailliertere Aufstellung der Subkomponenten im Modul Modell. Zur besseren Übersicht wird das Modul in die Komponenten Gierdynamik, Rad, Schwimmwinkel und Karosserie unterteilt. Die Komponente Gierdynamik berechnet die Gierrate, -geschwindigkeit und -beschleunigung, die zum einen als Eingänge für andere Komponenten eingehen und zum anderen im Modul Auswertung angezeigt werden sollen. Die Komponente Schwimmwinkel berechnet den Schwimmwinkel und dient damit als Eingang für weitere Komponenten. Die Komponente Rad kalkuliert die einzelnen Kräfte, die am Rad anliegen wie z.B. die Querkraft und die dafür nötigen Winkel wie z.B. Achs-Schräglaufwinkel und Achs-Schwimmwinkel. Die einzelnen Ausgänge aus dieser Subkomponente werden zur Anzeige im Modul Auswertung und als Eingänge für andere Komponenten benötigt. Im letzten Submodul Karoserie werden die insgesamt wirkenden Kräfte und Beschleunigungen in Quer- und Längsrichtung ermittelt. Auch diese Ausgänge werden sowohl als Eingänge für andere Komponenten, als auch für die Darstellung im Modul Auswertung verwertet. Wie die Berechnungen der einzelnen Werte erfolgt, wird im nächsten Kapitel Komponentenspezifikationen erläutert. | ||
[[Datei:Technischer_Systementwurf_Komponenten.PNG|links|mini|Abb 5: Technischer Systementwurf der Subkomponenten für das Lineare Einspurmodell]] | [[Datei:Technischer_Systementwurf_Komponenten.PNG|links|mini|Abb 5: Technischer Systementwurf der Subkomponenten für das Lineare Einspurmodell]] | ||
| Zeile 62: | Zeile 66: | ||
=== Komponentenspezifikation === | === Komponentenspezifikation === | ||
Dieses Kapitel bezieht sich vollständig auf die von Herrn Prof. Göbel zur Verfügung | Dieses Kapitel bezieht sich vollständig auf die von Herrn Prof. Göbel zur Verfügung gestellte Quelle <ref name="Einspurmodell"> Göbel, M.: ''Fahrwerkmanagement Skript'', Stand: 10.Juni.2020, Seite 12ff.</ref>. | ||
Zunächst erfolgt die Berechnung der Achs-Schwimmwinkel vorne und hinten mit | |||
Zunächst erfolgt die Berechnung der Achs-Schwimmwinkel vorne und hinten mit folgenden Formeln: | |||
<math>\beta_v = \beta + \frac{l_v \cdot _K\dot{\psi}}{_Kv_{Cx}} </math> | <math>\beta_v = \beta + \frac{l_v \cdot _K\dot{\psi}}{_Kv_{Cx}} </math> | ||
| Zeile 69: | Zeile 74: | ||
<math>\beta_h = \beta - \frac{l_h \cdot _K\dot{\psi}}{_Kv_{Cx}} </math> | <math>\beta_h = \beta - \frac{l_h \cdot _K\dot{\psi}}{_Kv_{Cx}} </math> | ||
Die benötigten Parameter hierfür, kommen entweder aus dem Parameterskript, dieses wird im Gesamtmodell erklärt, oder von anderen Subkomponenten deren Erläuterungen in diesem Kapitel erfolgen. Aus den Schwimmwinkeln vorne und hinten können die Achschräglaufwinkel durch folgende | Die benötigten Parameter hierfür, kommen entweder aus dem Parameterskript, dieses wird im Gesamtmodell erklärt, oder von anderen Subkomponenten deren Erläuterungen in diesem Kapitel erfolgen. Aus den Schwimmwinkeln vorne und hinten können die Achschräglaufwinkel durch folgende Formeln berechnet werden: | ||
<math>\alpha_v = \delta_v - \beta_v </math> | <math>\alpha_v = \delta_v - \beta_v </math> | ||
| Zeile 81: | Zeile 86: | ||
<math>_RF_{yh} = c_h \cdot \alpha_h</math> | <math>_RF_{yh} = c_h \cdot \alpha_h</math> | ||
Damit | Damit ist die Modellierung der Kräfte und Winkel am Rad abgeschlossen. Als nächstes werden die im Rad wirkenden Kräfte, zu in der Karosserie wirkenden Kräfte transformiert: | ||
<math>_KF_{xv} = \delta_v \cdot _RF_{yv}</math> | <math>_KF_{xv} = \delta_v \cdot _RF_{yv}</math> | ||
| Zeile 91: | Zeile 96: | ||
<math>_KF_{yh} = _RF_{yh}</math> | <math>_KF_{yh} = _RF_{yh}</math> | ||
Die | Die daraus resultierende gesamte Längs- und Querkraft ergibt sich aus den Formeln: | ||
<math>_KF_{Cx} = _KF_{xv} + _KF_{xh}</math> | <math>_KF_{Cx} = _KF_{xv} + _KF_{xh}</math> | ||
| Zeile 97: | Zeile 102: | ||
<math>_KF_{Cy} = _KF_{yv} + _KF_{yh}</math> | <math>_KF_{Cy} = _KF_{yv} + _KF_{yh}</math> | ||
Diese | Diese Formeln lassen sich in dieser Form nur anwenden, weil mit Winkeln << 1 gerechnet wird. Für größere Winkel müssen entsprechende trigonometrische Zusammenhänge berücksichtigt werden. Weiterhin kann die Querbeschleunigung aus der Querkraft berechnet werden. Die Formel hierfür lässt sich aus dem Schwerpunktsatz bestimmen: | ||
<math> m \cdot _Ka_{Cy} = _KF_{yv} + _KF_{yh}</math> | <math> m \cdot _Ka_{Cy} = _KF_{yv} + _KF_{yh}</math> | ||
| Zeile 106: | Zeile 111: | ||
Dadurch ist die Modellierung der Karoserie vollständig. | Dadurch ist die Modellierung der Karoserie vollständig. | ||
Das nächste | Das nächste Vorgehen ist die Bestimmung der Gierdynamik. Dies geschieht durch den Drallsatz der wie folgt lautet: | ||
<math>J_{zz} \cdot _K\ddot{\psi} = l_v \cdot _KF_{yv} - l_h \cdot _KF_{yh}</math> | <math>J_{zz} \cdot _K\ddot{\psi} = l_v \cdot _KF_{yv} - l_h \cdot _KF_{yh}</math> | ||
Wie bereits erwähnt wird von kleinen Winkeln ausgegangen, weshalb die Querkräfte am Rad auch den Querkräften in Fahrzeugkoordinaten entsprechen. Durch Umformung und Integration des Drallsatzes lassen sich Giergeschwindigkeit, und Gierwinkel ebenfalls bestimmen, die als Eingänge für weitere Subkomponenten und zur Auswertung dienen. Die umgestellten Formeln lauten: | Wie bereits erwähnt, wird von kleinen Winkeln ausgegangen, weshalb die Querkräfte am Rad auch den Querkräften in Fahrzeugkoordinaten entsprechen. Durch Umformung und Integration des Drallsatzes lassen sich Giergeschwindigkeit, und Gierwinkel ebenfalls bestimmen, die als Eingänge für weitere Subkomponenten und zur Auswertung dienen. Die umgestellten Formeln lauten: | ||
Zur Gierbeschleunigung: | Zur Gierbeschleunigung: | ||
| Zeile 124: | Zeile 129: | ||
<math>_K{\psi} = \int\int\frac{l_v \cdot _KF_{yv} - l_h \cdot _KF_{yh}}{J_{zz}} dt^2</math> | <math>_K{\psi} = \int\int\frac{l_v \cdot _KF_{yv} - l_h \cdot _KF_{yh}}{J_{zz}} dt^2</math> | ||
Die letzte fehlende Komponente ist die des | Die letzte fehlende Komponente ist die des Schwimmwinkels, welche als Eingang für die Radkräfte benötigt wird. Der Schwimmwinkel lässt sich aus dem Schwerpunktsatz im Bahnsystem nach Newton herleiten. Dieser lautet: | ||
<math> m \cdot (_K\dot{\beta} +_K\dot{\psi}) \cdot _Kv_{Cx} = _KF_{Cy}</math> | <math> m \cdot (_K\dot{\beta} +_K\dot{\psi}) \cdot _Kv_{Cx} = _KF_{Cy}</math> | ||
| Zeile 132: | Zeile 137: | ||
<math>_K{\beta} = \int (\frac{_KF_{Cy}}{m \cdot _Kv_{Cx}} - _K\dot{\psi}) dt </math> | <math>_K{\beta} = \int (\frac{_KF_{Cy}}{m \cdot _Kv_{Cx}} - _K\dot{\psi}) dt </math> | ||
Auch hier kann dies nur so vorgenommen werden, weil mit kleinem Winkel und keiner Verkippung des Fahrzeugs gerechnet wird. Damit ist die Komponentenspezifikation abgeschlossen. Die dokumentierte | Auch hier kann dies nur so vorgenommen werden, weil mit kleinem Winkel und keiner Verkippung des Fahrzeugs gerechnet wird. Damit ist die Komponentenspezifikation abgeschlossen. Die dokumentierte Komponentenspezifikation ist unter diesem [https://svn.hshl.de/svn/BSE_SystemsDesignEng/trunk/Projekte/ESM_SS2021/Gruppen/Gruppe%20F/04_Komponentenspezifikation/ Link] abrufbar. | ||
=== Gesamtmodell === | === Gesamtmodell === | ||
Mit Abschluss der Komponentenspezifikation kann das holotische Lineare Einspurmodell in Simulink umgesetzt werden. Zur Verdeutlichung der Umsetzung der aus vorherigen Kapitel ermittelten Formeln, zeigt Abbildung 6 beispielhaft die Herangehensweise für die Komponente Gierdynamik. Die gelben Bausteine sind die Eingänge des Submoduls und die grünen entsprechen den Ausgängen. Die Pfeile zeigen die Verbindungen mit den Blöcken an, welche die abgebildete Rechenoperation durchführen. So werden sukzessiv die Formeln „gebaut“. Die beiden rechten Baukästen sind Integratorblöcke und führen entsprechend Integrationen durch. So wird aus der Gierbeschleunigung, die Giergeschwindigkeit und durch weitere Integration der Gierwinkel. Dieses Schema kann in allen Subkomponenten erkannt werden. | Mit Abschluss der Komponentenspezifikation kann das holotische Lineare Einspurmodell in Simulink umgesetzt werden. Zur Verdeutlichung der Umsetzung der aus vorherigen Kapitel ermittelten Formeln, zeigt Abbildung 6 beispielhaft die Herangehensweise für die Komponente Gierdynamik. Die gelben Bausteine sind die Eingänge des Submoduls und die grünen entsprechen den Ausgängen. Die Pfeile zeigen die Verbindungen mit den Blöcken an, welche die abgebildete Rechenoperation durchführen. So werden sukzessiv die Formeln „gebaut“. Die beiden rechten Baukästen sind Integratorblöcke und führen entsprechend Integrationen durch. So wird aus der Gierbeschleunigung, die Giergeschwindigkeit und durch weitere Integration ergibt sich der Gierwinkel. Dieses Schema kann in allen Subkomponenten erkannt werden. | ||
[[Datei:Beispielumsetzung_Simulink_Gierdynamik.PNG|links|mini|Abb 6: Beispielumsetzung im Simulink umgesetzter Formeln mit Integration]] | [[Datei:Beispielumsetzung_Simulink_Gierdynamik.PNG|links|mini|Abb 6: Beispielumsetzung im Simulink umgesetzter Formeln mit Integration]] | ||
<br clear=all> | <br clear=all> | ||
Im Gesamtmodell können im bereits erwähnten Scope die Signale ausgewertet werden. Das Scope und die entsprechenden Graphen sind in Abbildung 7 zu erkennen. So werden in den einzelnen Graphen bestimmte Signale zusammengefasst und in einem Koordinatensystem abgebildet. Im oberen linken Rechteck werden die insgesamt wirkenden Kräfte | Im Gesamtmodell können im bereits erwähnten Scope die Signale ausgewertet werden. Das Scope und die entsprechenden Graphen sind in Abbildung 7 zu erkennen. So werden in den einzelnen Graphen bestimmte Signale zusammengefasst und in einem Koordinatensystem abgebildet. Im oberen linken Rechteck werden die insgesamt wirkenden Kräfte dargestellt. Darunter erfolgt die Darstellung Schräglaufwinkel und darunter die Schwimmwinkel (jeweils vorne und hinten in Rad). Oben rechts werden die drei Signale Gierbeschleunigung, Giergeschwindigkeit und Gierwinkel zusammen gezeigt (ebenfalls in Rad) und zum Schluss wird die Querbeschleunigung in einem Koordinatensystem dargestellt. Damit sind alle geforderten Ausgänge aus dem Lastenheft veranschaulicht. | ||
[[Datei:Scope_Auswertung.PNG|links|mini|Abb 7: Koordinatensysteme zur Auswertung der berechneten Signale aus dem linearen Einspurmodell]] | [[Datei:Scope_Auswertung.PNG|links|mini|Abb 7: Koordinatensysteme zur Auswertung der berechneten Signale aus dem linearen Einspurmodell]] | ||
<br clear=all> | <br clear=all> | ||
Weiterhin erlaubt die Simulation zwischen | Weiterhin erlaubt die Simulation zwischen drei verschiedenen Fahrmanövern zu wechseln. Abbildung 8 zeigt die Umsetzung dieser in Simulink. Über ein Skript, (die Anwendung dieses wird im Kapitel Anwendung erläutert) wird das gewünschte Manöver ausgewählt. Es ist möglich eine Slalomfahrt (Manöver 1), ein plötzliches Einlenken nach zehn Sekunden (Manöver 2) oder ein von Beginn an wirkendes Lenkverhalten einzustellen. Das Modell könnte auch um beliebig viele Einstellverhalten erweitert werden, zur Übersichtlichkeit wurden nur diese drei Fahrmanöver gewählt. Es kann ebenfalls eingestellt werden, ob eine Hinterachslenkung simuliert werden soll. Diese entspricht einem im Skript definierten Verhältnis zwischen Vorder- und Hinterachslenkung. Initial wird diese mit Null bestimmt (also keiner Hinterachslenkung). | ||
[[Datei:Manöversteuerung.PNG|links|mini|Abb 8: Umsetzung der Manöversteuerung im Simulink]] | [[Datei:Manöversteuerung.PNG|links|mini|Abb 8: Umsetzung der Manöversteuerung im Simulink]] | ||
| Zeile 152: | Zeile 157: | ||
Alle Parameter können entweder über ein MATLAB Skript oder eine MATLAB GUI geladen werden. Wie diese angewendet werden und auch wie die Simulation insgesamt angewendet wird, zeigt Kapitel Anwendung. Das vollständige Modell kann in diesem [https://svn.hshl.de/svn/BSE_SystemsDesignEng/trunk/Projekte/ESM_SS2021/Gruppen/Gruppe%20F/05_Entwicklung/ Link] eingesehen werden. | Alle Parameter können entweder über ein MATLAB Skript oder eine MATLAB GUI geladen werden. Wie diese angewendet werden und auch wie die Simulation insgesamt angewendet wird, zeigt Kapitel Anwendung. Das vollständige Modell kann in diesem [https://svn.hshl.de/svn/BSE_SystemsDesignEng/trunk/Projekte/ESM_SS2021/Gruppen/Gruppe%20F/05_Entwicklung/ Link] eingesehen werden. | ||
== Modelltest == | == Modelltest == | ||
Der Modelltest besteht darin, das gesamte System stufenweise zu testen, um mögliche Fehler oder Unstimmigkeiten zu identifizieren. Dazu wird zunächst der Komponententest, dann der Integrationstest und zum Schluss der Systemtest durchgeführt. Für die Testung werden stets Eingänge initialisiert, um die daraus resultierenden Ausgaben mit den erwartenden Ergebnissen zu vergleichen. Weichen die Ergebnisse voneinander ab, so werden die möglichen Fehler identifiziert und in Kommentaren ausformuliert. | |||
=== Komponententest === | === Komponententest === | ||
In dem Komponententest werden alle in dem gesamten System befindlichen Komponenten näher betrachtet. Dazu werden die Komponenten: Gierdynamik, Karosserie, Rad und Schwimmwinkel auf die korrekte Funktionalität überprüft, indem jede Komponente gleichermaßen auf verschiedene Testfälle simuliert wird. | |||
Folgend wird die Gierdynamik repräsentativ für die weiteren Komponenten näher betrachtet und erläutert. | |||
Wie in Abbildung 9 dargestellt, werden alle Eingänge für den ersten Testfall gleich Null gesetzt. Das Ergebnis stimmt mit dem erwarteten Ergebnis überein, da die Ausgänge keine Ausgabe ergeben. | |||
[[Datei:Abb1.png|links|mini|Abb 9: Testfall 1 vom Komponententest am Beispiel der Gierdynamik]] | |||
<br clear=all> | |||
Werden alle Eingänge gleich Eins gesetzt, so ergeben die Ausgänge den zu erwartenden Wert Null (vgl. Abbildung 10). | |||
[[Datei:Abb2.png|links|mini|Abb 10: Testfall 2 vom Komponententest am Beispiel der Gierdynamik]] | |||
<br clear=all> | |||
Im letzten Testfall werden den Eingängen beispielwerte aus der Aufgabenstellung der Seminaraufgabe <ref name="Seminaraufgabe"> Göbel, M.: ''Systems Design Engineering Vorlesung & Seminar''.</ref> eingegeben. Wie auch hier stimmen die erwartenden Ergebnisse mit dem tatsächlichen Ergebnis aus dem Testfall (siehe Abbildung 11) überein. | |||
[[Datei:Testfall3.png|links|mini|Abb 11: Testfall 3 vom Komponententest am Beispiel der Gierdynamik]] | |||
<br clear=all> | |||
=== Integrationstest === | === Integrationstest === | ||
Der Integrationstest umfasst die Überprüfung der drei Modelle: Manöversteuerung, Modell und die Auswertung. Die Eingänge gleichen den drei Testfällen des Komponententests. In dem Integrationstest wird darüber hinaus der Reihe nach ein Sinus-, Sprung- und Konstant-Verhalten, jeweils mit den drei Testfällen auf die korrekte Funktionsweise untersucht. | |||
Der Integrationstest beginnt mit der Testung der Manöversteuerung. | |||
Im ersten Testfall werden alle Eingänge gleich Null gesetzt, was dazu führt, dass alle Ausgänge für alle drei Verhalten keine Ergebnisse ergeben (siehe SVN [https://svn.hshl.de/svn/BSE_SystemsDesignEng/trunk/Projekte/ESM_SS2021/Gruppen/Gruppe%20G/07_Integrationstest/ Link] | |||
). | |||
Werden allen Eingängen der Wert Eins zugewiesen, so ergibt die Simulation die in Abbildung 12 dargestellten Ergebnisse. | |||
[[Datei:Testfall2Sinus-Verhalten.png|links|mini|Abb 12: Testfall 2 Sinus-Verhalten Manöversteuerung]] | |||
<br clear=all> | |||
Das Testen des Sprung- und Konstant-Verhaltens ergibt ähnliche Ausgangswerte, mit dem Unterschied, dass lw_v beim Sprung-Verhalten einen Sprung auf den Wert 1 macht und bei dem letzteren Verhalten lw_v konstant den Wert 1 annimmt (siehe SVN [https://svn.hshl.de/svn/BSE_SystemsDesignEng/trunk/Projekte/ESM_SS2021/Gruppen/Gruppe%20G/07_Integrationstest/ Link] | |||
). | |||
Anschließend werden allen Eingängen für jedes Verhalten feste beispielwerte aus der Quelle <ref name="Seminaraufgabe"> Göbel, M.: ''Systems Design Engineering Vorlesung & Seminar''.</ref> zugewiesen. Die Ergebnisse der Testfälle führen zu den erwarteten Ergebnissen (siehe SVN [https://svn.hshl.de/svn/BSE_SystemsDesignEng/trunk/Projekte/ESM_SS2021/Gruppen/Gruppe%20G/07_Integrationstest/ Link]) | |||
. | |||
Die Testung des Modells basiert auf der gleichen Vorgehensweise wie die bereits erläuterte Testung der Manöversteuerung. Der Unterschied liegt darin, dass die Längsgeschwindigkeit mit dem Wert 10 und der Lenkwinkel vorne mit 0,4 (für das Testverhalten der Sinuskurve ist Lenkwinkel vorne = 0,4*sin) deklariert wird. Alle Testfälle des Modells führen zu den erwarteten Ergebnissen. | |||
Der Integrationstest schließt mit Überprüfung der Auswertung ab. In diesem Test werden auf gleicherweise für Testfall 1 alle Eingänge gleich Null gesetzt, für Testfall 2 alle Eingänge gleich Eins und für Testfall 3 werden die beispielwerte aus der Aufgabenstellung (Quelle <ref name="Seminaraufgabe"> Göbel, M.: ''Systems Design Engineering Vorlesung & Seminar''.</ref>) geladen. Alle Ergebnisse werden mithilfe von Scopes visuell dargestellt und ergeben in allen Testfällen korrekte Ergebnisse (siehe SVN [https://svn.hshl.de/svn/BSE_SystemsDesignEng/trunk/Projekte/ESM_SS2021/Gruppen/Gruppe%20G/07_Integrationstest/ Link] | |||
). | |||
=== Systemtest === | === Systemtest === | ||
Der finale Systemtest überprüft das Gesamtsystem. Es werden alle Module verknüpft und ihre Funktionalität wird getestet. Die Vorgehensweise entspricht dem des Komponenten- und Integrationstests. Es werden die drei Verhalten Sinus-, Sprung-, und Konstant-Verhalten mit den drei Testfällen Eingänge = 0, Eingänge = 1, Eingänge mit Beispielwerten ausgewertet. | |||
Insgesamt verläuft der Systemtest positiv und es sind keine Fehler aufgetreten. Dies ist auch das zu erwartenden Ergebnis, da bereits im Komponenten- und Integrationstest keine Auffälligkeiten vorhanden sind. Der vollständige Systemtest ist unter diesem Link abrufbar. | |||
== Anwendung == | == Anwendung == | ||
Für die Simulation wird zunächst die Parameterdatei geladen und gestartet. Alternativ kann auch die MATLAB GUI verwendet werden, um die Parameter und verschiedene Einstellungen zu laden und zu starten. Die Simulation muss jedoch noch im MATLAB Simulink gestartet werden. Entsprechende Einstellungen, wie beispielsweise die Schrittweite und die Simulationsdauer wurden bereits vordefiniert. Die Ergebnisse können im Modul Auswertung in den Scopes visualisiert werden. | |||
=== Parameterdatei === | === Parameterdatei === | ||
Die Parameterdatei ist wesentlicher Bestandteil der gesamten Anwendung. In der Datei werden benötigte Eingabewerte des Modells deklariert. Dazu gehören wie in Abbildung 13 dargestellt, die Werte die für die Manöversteuerung relevant sind und die Werte für das Modul Modell. Ebenso kann durch das ausführen der Parameterdatei das Simulink Modell geöffnet werden. | |||
[[Datei:Parameterdatei.png|links|mini|Abb 13: Parameterdatei]] | |||
<br clear=all> | |||
< | |||
=== MATLAB GUI === | |||
Die erstellte MATLAB GUI (Abbildung 14) ist eine Erweiterung der Parameterdatei. Dem Anwender wird es ermöglicht unter der Rubrik Fahrmanöver verschiedene Manöver auszuwählen. Ebenso kann der Lenkwinkel, das Übersetzungsverhältnis des vorderen- zu hinteren Lenkwinkels und die Längsgeschwindigkeit angepasst werden. Des Weiteren können die Fahrzeugeigenschaften Achssteifigkeiten, Massenträgheit, Abstände und Masse variiert werden. Unter der Rubrik Simulation initialisieren kann das Simulink Modell durch die GUI geöffnet und die Simulation geladen werden. | |||
[[Datei:MATLABGUI.png|links|mini|Abb 14: MATLAB GUI]] | |||
<br clear=all> | |||
== Fazit == | == Fazit == | ||
Das lineare Einspurmodell ist ein komplexes Thema und erfordert weitreichende ingenieurswissenschaftliche Kenntnisse insbesondere in der Automobiltechnik. | |||
Durch die Aufgabe konnten vertiefte Fachkenntnisse in der Anwendung des V-Modells erlangt und bereits vorhandene Fähigkeiten aus vorherigen Modulen erweitert und angewendet werden. Insbesondere wurden die Softwarefähigkeiten durch die Anwendung von MATLAB Simulink weitestgehend gesteigert. | |||
Zusammenfassend lässt sich festhalten, dass die Erstellung des Lastenhefts mit besonderer Sorgfalt erstellt werden musste, da dieses Dokument die Basis der gesamten Arbeit bildet. | |||
Ebenfalls wurde festgestellt, dass die Erstellung der Komponentenspezifikation sich als schwierig herausstellte. Die Modellierung ist aufgrund der geforderten Simulink Kenntnisse und dem Umfang der benötigten Formeln sehr komplex. Jedoch konnten alle auftretenden Schwierigkeiten aufgrund der ausreichend gegebenen Zeit gelöst werden. | |||
Dem Anwender wird es ermöglicht, mithilfe des lineare Einspurmodells, jegliches lineare Fahrverhalten durch Anpassung der Fahrzeugeigenschaften und des Fahrverhaltens zu simulieren. | |||
Demzufolge konnte die Seminaraufgabe, das lineare Einspurmodell nach dem V-Modell zu konzipieren und zu modellieren, insgesamt erfolgreich abgeschlossen werden. | |||
== Literaturverzeichnis == | == Literaturverzeichnis == | ||
<references /> | <references /> | ||
→ zurück zum Hauptartikel: [["Systems Design Engineering" - Seminaraufgabe SoSe 2021: Einspurmodell“]] | |||
Aktuelle Version vom 12. Juli 2021, 08:25 Uhr
→ zurück zum Hauptartikel: "Systems Design Engineering" - Seminaraufgabe SoSe 2021: Einspurmodell“
Autoren: Daniel Schwarz, Maik Kleinspohn
Einleitung
Teil des Moduls Systems Design Engineering im Studiengang Business and Systems Engineering ist die Seminaraufgabe, mit Themenschwerpunkt der Modellierung des linearen Einspurmodells. Das Modell soll meilensteinweise nach dem Vorgehen des V-Modells konzipiert, programmiert und getestet werden. Das Skript [1] gibt eine Übersicht der genauen Aufgabenstellung, wie auch die Rahmenbedingung der Seminaraufgabe.
Entwicklungsprozess
Wie bereits in der Einleitung erwähnt wird nach dem V-Modell vorgegangen. Die wesentlichen Schritte zur Entwicklung des linearen Einspurmodells werden im folgendem näher erläutert. Zuerst müssen die Rahmenbedingungen festgelegt werden. Dies erfolgt in der Anforderungsdefinition. Darauf aufbauend wird der funktionale Systementwurf erstellt, welcher den Rahmen zur Entwicklung vorgibt. Daraufhin werden mit dem technischen Systementwurf, benötigte Submodule und Ein- und Ausgänge der Module bestimmt. Im nächsten Schritt werden Komponenten der Submodule mithilfe der Komponentenspezifikation erstellt. Zuletzt zeigt dieses Kapitel das Gesamtmodell, welches in MATLAB Simulink erzeugt wurde. Die Validierung des Modells und wie es anzuwenden ist, erfolgt in den darauffolgenden Hauptkapiteln.
Anforderungsdefinition
Um die Rahmenbedingungen festzulegen wird mit einem Lastenheft gearbeitet. Das vollständige Lastenheft kann unter diesem Link eingesehen werden. Das Lastenheft wird in fünf Kapitel unterteilt. In Abbildung 1 sind allgemeine Kriterien aus dem Lastenheft dargestellt. Dort wird z.B. festgelegt, dass Arbeitsergebnisse im SVN hochgeladen werden.

In Abbildung 2 ist zu erkennen, dass technische Grundbedingungen protokoliert werden. Diese bestimmen z.B. die Paramater, siehe Anforderungs-ID 18 „Es müssen die Parameter Massenträgheit, Radstand, Schwerpunktabstand zur Vorderachse, Masse, Achssteifigkeit vorne und hinten berücksichtigt werden.“ oder auch die Darstellung, siehe Anforderungs-ID 23 „Die Diagramme müssen vertikal übereinander dargestellt werden.“.

Insgesamt umfasst das Lastenheft 47 Anforderungen die in die Kapitel
- Allgemein
- Abgaben
- Technisch
- Eingänge
- Ausgänge
- Parameter
- Software/Werkzeuge
- Nachhaltigkeit/Dokumentation
untergliedert sind.
Dieses Dokument legt die Grundvoraussetzung für das Modell. Im Laufe der Entwicklung kann es vorkommen, dass einzelne Anforderungen angepasst oder die Liste erweitert/verkürzt werden muss. Das Dokument im obigen Link entspricht dem Endstand des Lastenheft und kann zur Messung des Modells herangezogen werden.
Funktionaler Systementwurf
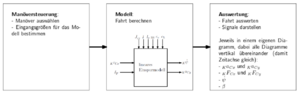
Der funktionale Systementwurf wird durch Herrn Prof. Göbel vorgegeben und kann Abbildung 3 entnommen werden. Zu sehen sind die drei Module Manöversteuerung, Modell und Auswertung. Im Modul Manöversteuerung werden in der späteren Programmierung die Fahrmanöver und Eingangsgrößen wie Längsgeschwindigkeit und Lenkwinkel in die Simulation geladen. Das Modul Modell umfasst alle Berechnungen, die für das lineare Einspurmodell nötig sind. Auf dieses wird in den folgenden Unterkapiteln noch näher eingegangen. Im letzten Modul Auswertung werden dann die errechneten Werte grafisch dargestellt. Die Darstellungen werden in späteren Unterkapiteln gezeigt. Der funktionale Systementwurf ist in Quelle [1] enthalten.
Technischer Systementwurf
Im technischen Systementwurf erfolgt die Umsetzung des funktionalen Systementwurf in Simulink. Für die drei Hauptmodule ist der Systementwurf in Abbildung 4 zusehen. Wie es im funktionalen Systementwurf bestimmt wurde, kommen aus dem Modul Manöversteuerung die Längsgeschwindigkeit und die Lenkwinkel für die Vorder- und Hinterachse (falls vorhanden, sonst ist dieser Wert = 0). Im Modul Modell werden diese Eingaben weiterverarbeitet und anschließend zu den Ausgängen, die im Lastenheft bestimmt werden, verrechnet. Zuletzt erfolgt die grafische Darstellung mit einem Scope im Modul Auswertung.
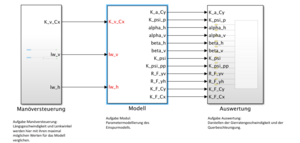
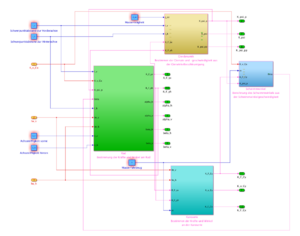
Abbildung 5 zeigt eine detailliertere Aufstellung der Subkomponenten im Modul Modell. Zur besseren Übersicht wird das Modul in die Komponenten Gierdynamik, Rad, Schwimmwinkel und Karosserie unterteilt. Die Komponente Gierdynamik berechnet die Gierrate, -geschwindigkeit und -beschleunigung, die zum einen als Eingänge für andere Komponenten eingehen und zum anderen im Modul Auswertung angezeigt werden sollen. Die Komponente Schwimmwinkel berechnet den Schwimmwinkel und dient damit als Eingang für weitere Komponenten. Die Komponente Rad kalkuliert die einzelnen Kräfte, die am Rad anliegen wie z.B. die Querkraft und die dafür nötigen Winkel wie z.B. Achs-Schräglaufwinkel und Achs-Schwimmwinkel. Die einzelnen Ausgänge aus dieser Subkomponente werden zur Anzeige im Modul Auswertung und als Eingänge für andere Komponenten benötigt. Im letzten Submodul Karoserie werden die insgesamt wirkenden Kräfte und Beschleunigungen in Quer- und Längsrichtung ermittelt. Auch diese Ausgänge werden sowohl als Eingänge für andere Komponenten, als auch für die Darstellung im Modul Auswertung verwertet. Wie die Berechnungen der einzelnen Werte erfolgt, wird im nächsten Kapitel Komponentenspezifikationen erläutert.
Der gesamte technische Systementwurf kann in diesem Link eingesehen werden.
Komponentenspezifikation
Dieses Kapitel bezieht sich vollständig auf die von Herrn Prof. Göbel zur Verfügung gestellte Quelle [2].
Zunächst erfolgt die Berechnung der Achs-Schwimmwinkel vorne und hinten mit folgenden Formeln:
Die benötigten Parameter hierfür, kommen entweder aus dem Parameterskript, dieses wird im Gesamtmodell erklärt, oder von anderen Subkomponenten deren Erläuterungen in diesem Kapitel erfolgen. Aus den Schwimmwinkeln vorne und hinten können die Achschräglaufwinkel durch folgende Formeln berechnet werden:
Unter Hinzuziehung der Achssteifigkeiten können mit den Achsschräglaufwinkel die Querkräfte am Rad wie folgt bestimmt werden:
Damit ist die Modellierung der Kräfte und Winkel am Rad abgeschlossen. Als nächstes werden die im Rad wirkenden Kräfte, zu in der Karosserie wirkenden Kräfte transformiert:
Die daraus resultierende gesamte Längs- und Querkraft ergibt sich aus den Formeln:
Diese Formeln lassen sich in dieser Form nur anwenden, weil mit Winkeln << 1 gerechnet wird. Für größere Winkel müssen entsprechende trigonometrische Zusammenhänge berücksichtigt werden. Weiterhin kann die Querbeschleunigung aus der Querkraft berechnet werden. Die Formel hierfür lässt sich aus dem Schwerpunktsatz bestimmen:
Umgeformt zu :
Dadurch ist die Modellierung der Karoserie vollständig. Das nächste Vorgehen ist die Bestimmung der Gierdynamik. Dies geschieht durch den Drallsatz der wie folgt lautet:
Wie bereits erwähnt, wird von kleinen Winkeln ausgegangen, weshalb die Querkräfte am Rad auch den Querkräften in Fahrzeugkoordinaten entsprechen. Durch Umformung und Integration des Drallsatzes lassen sich Giergeschwindigkeit, und Gierwinkel ebenfalls bestimmen, die als Eingänge für weitere Subkomponenten und zur Auswertung dienen. Die umgestellten Formeln lauten:
Zur Gierbeschleunigung:
Zur Giergeschwindigkeit:
Zum Gierwinkel:
Die letzte fehlende Komponente ist die des Schwimmwinkels, welche als Eingang für die Radkräfte benötigt wird. Der Schwimmwinkel lässt sich aus dem Schwerpunktsatz im Bahnsystem nach Newton herleiten. Dieser lautet:
Dieser wird umgestellt zu:
Auch hier kann dies nur so vorgenommen werden, weil mit kleinem Winkel und keiner Verkippung des Fahrzeugs gerechnet wird. Damit ist die Komponentenspezifikation abgeschlossen. Die dokumentierte Komponentenspezifikation ist unter diesem Link abrufbar.
Gesamtmodell
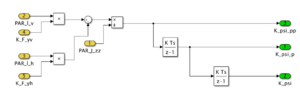
Mit Abschluss der Komponentenspezifikation kann das holotische Lineare Einspurmodell in Simulink umgesetzt werden. Zur Verdeutlichung der Umsetzung der aus vorherigen Kapitel ermittelten Formeln, zeigt Abbildung 6 beispielhaft die Herangehensweise für die Komponente Gierdynamik. Die gelben Bausteine sind die Eingänge des Submoduls und die grünen entsprechen den Ausgängen. Die Pfeile zeigen die Verbindungen mit den Blöcken an, welche die abgebildete Rechenoperation durchführen. So werden sukzessiv die Formeln „gebaut“. Die beiden rechten Baukästen sind Integratorblöcke und führen entsprechend Integrationen durch. So wird aus der Gierbeschleunigung, die Giergeschwindigkeit und durch weitere Integration ergibt sich der Gierwinkel. Dieses Schema kann in allen Subkomponenten erkannt werden.
Im Gesamtmodell können im bereits erwähnten Scope die Signale ausgewertet werden. Das Scope und die entsprechenden Graphen sind in Abbildung 7 zu erkennen. So werden in den einzelnen Graphen bestimmte Signale zusammengefasst und in einem Koordinatensystem abgebildet. Im oberen linken Rechteck werden die insgesamt wirkenden Kräfte dargestellt. Darunter erfolgt die Darstellung Schräglaufwinkel und darunter die Schwimmwinkel (jeweils vorne und hinten in Rad). Oben rechts werden die drei Signale Gierbeschleunigung, Giergeschwindigkeit und Gierwinkel zusammen gezeigt (ebenfalls in Rad) und zum Schluss wird die Querbeschleunigung in einem Koordinatensystem dargestellt. Damit sind alle geforderten Ausgänge aus dem Lastenheft veranschaulicht.

Weiterhin erlaubt die Simulation zwischen drei verschiedenen Fahrmanövern zu wechseln. Abbildung 8 zeigt die Umsetzung dieser in Simulink. Über ein Skript, (die Anwendung dieses wird im Kapitel Anwendung erläutert) wird das gewünschte Manöver ausgewählt. Es ist möglich eine Slalomfahrt (Manöver 1), ein plötzliches Einlenken nach zehn Sekunden (Manöver 2) oder ein von Beginn an wirkendes Lenkverhalten einzustellen. Das Modell könnte auch um beliebig viele Einstellverhalten erweitert werden, zur Übersichtlichkeit wurden nur diese drei Fahrmanöver gewählt. Es kann ebenfalls eingestellt werden, ob eine Hinterachslenkung simuliert werden soll. Diese entspricht einem im Skript definierten Verhältnis zwischen Vorder- und Hinterachslenkung. Initial wird diese mit Null bestimmt (also keiner Hinterachslenkung).
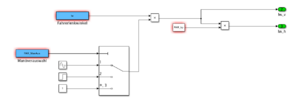
Alle Parameter können entweder über ein MATLAB Skript oder eine MATLAB GUI geladen werden. Wie diese angewendet werden und auch wie die Simulation insgesamt angewendet wird, zeigt Kapitel Anwendung. Das vollständige Modell kann in diesem Link eingesehen werden.
Modelltest
Der Modelltest besteht darin, das gesamte System stufenweise zu testen, um mögliche Fehler oder Unstimmigkeiten zu identifizieren. Dazu wird zunächst der Komponententest, dann der Integrationstest und zum Schluss der Systemtest durchgeführt. Für die Testung werden stets Eingänge initialisiert, um die daraus resultierenden Ausgaben mit den erwartenden Ergebnissen zu vergleichen. Weichen die Ergebnisse voneinander ab, so werden die möglichen Fehler identifiziert und in Kommentaren ausformuliert.
Komponententest
In dem Komponententest werden alle in dem gesamten System befindlichen Komponenten näher betrachtet. Dazu werden die Komponenten: Gierdynamik, Karosserie, Rad und Schwimmwinkel auf die korrekte Funktionalität überprüft, indem jede Komponente gleichermaßen auf verschiedene Testfälle simuliert wird. Folgend wird die Gierdynamik repräsentativ für die weiteren Komponenten näher betrachtet und erläutert. Wie in Abbildung 9 dargestellt, werden alle Eingänge für den ersten Testfall gleich Null gesetzt. Das Ergebnis stimmt mit dem erwarteten Ergebnis überein, da die Ausgänge keine Ausgabe ergeben.
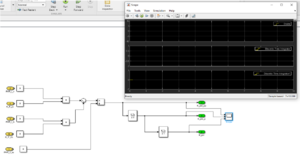
Werden alle Eingänge gleich Eins gesetzt, so ergeben die Ausgänge den zu erwartenden Wert Null (vgl. Abbildung 10).
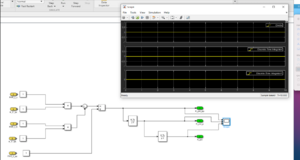
Im letzten Testfall werden den Eingängen beispielwerte aus der Aufgabenstellung der Seminaraufgabe [1] eingegeben. Wie auch hier stimmen die erwartenden Ergebnisse mit dem tatsächlichen Ergebnis aus dem Testfall (siehe Abbildung 11) überein.
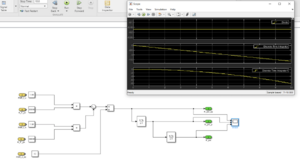
Integrationstest
Der Integrationstest umfasst die Überprüfung der drei Modelle: Manöversteuerung, Modell und die Auswertung. Die Eingänge gleichen den drei Testfällen des Komponententests. In dem Integrationstest wird darüber hinaus der Reihe nach ein Sinus-, Sprung- und Konstant-Verhalten, jeweils mit den drei Testfällen auf die korrekte Funktionsweise untersucht. Der Integrationstest beginnt mit der Testung der Manöversteuerung. Im ersten Testfall werden alle Eingänge gleich Null gesetzt, was dazu führt, dass alle Ausgänge für alle drei Verhalten keine Ergebnisse ergeben (siehe SVN Link ). Werden allen Eingängen der Wert Eins zugewiesen, so ergibt die Simulation die in Abbildung 12 dargestellten Ergebnisse.
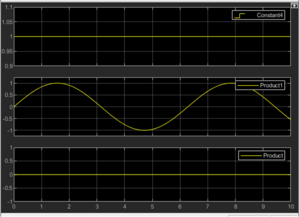
Das Testen des Sprung- und Konstant-Verhaltens ergibt ähnliche Ausgangswerte, mit dem Unterschied, dass lw_v beim Sprung-Verhalten einen Sprung auf den Wert 1 macht und bei dem letzteren Verhalten lw_v konstant den Wert 1 annimmt (siehe SVN Link
).
Anschließend werden allen Eingängen für jedes Verhalten feste beispielwerte aus der Quelle [1] zugewiesen. Die Ergebnisse der Testfälle führen zu den erwarteten Ergebnissen (siehe SVN Link)
.
Die Testung des Modells basiert auf der gleichen Vorgehensweise wie die bereits erläuterte Testung der Manöversteuerung. Der Unterschied liegt darin, dass die Längsgeschwindigkeit mit dem Wert 10 und der Lenkwinkel vorne mit 0,4 (für das Testverhalten der Sinuskurve ist Lenkwinkel vorne = 0,4*sin) deklariert wird. Alle Testfälle des Modells führen zu den erwarteten Ergebnissen.
Der Integrationstest schließt mit Überprüfung der Auswertung ab. In diesem Test werden auf gleicherweise für Testfall 1 alle Eingänge gleich Null gesetzt, für Testfall 2 alle Eingänge gleich Eins und für Testfall 3 werden die beispielwerte aus der Aufgabenstellung (Quelle [1]) geladen. Alle Ergebnisse werden mithilfe von Scopes visuell dargestellt und ergeben in allen Testfällen korrekte Ergebnisse (siehe SVN Link
).
Systemtest
Der finale Systemtest überprüft das Gesamtsystem. Es werden alle Module verknüpft und ihre Funktionalität wird getestet. Die Vorgehensweise entspricht dem des Komponenten- und Integrationstests. Es werden die drei Verhalten Sinus-, Sprung-, und Konstant-Verhalten mit den drei Testfällen Eingänge = 0, Eingänge = 1, Eingänge mit Beispielwerten ausgewertet. Insgesamt verläuft der Systemtest positiv und es sind keine Fehler aufgetreten. Dies ist auch das zu erwartenden Ergebnis, da bereits im Komponenten- und Integrationstest keine Auffälligkeiten vorhanden sind. Der vollständige Systemtest ist unter diesem Link abrufbar.
Anwendung
Für die Simulation wird zunächst die Parameterdatei geladen und gestartet. Alternativ kann auch die MATLAB GUI verwendet werden, um die Parameter und verschiedene Einstellungen zu laden und zu starten. Die Simulation muss jedoch noch im MATLAB Simulink gestartet werden. Entsprechende Einstellungen, wie beispielsweise die Schrittweite und die Simulationsdauer wurden bereits vordefiniert. Die Ergebnisse können im Modul Auswertung in den Scopes visualisiert werden.
Parameterdatei
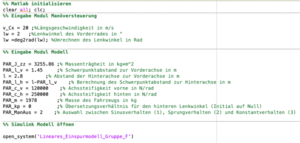
Die Parameterdatei ist wesentlicher Bestandteil der gesamten Anwendung. In der Datei werden benötigte Eingabewerte des Modells deklariert. Dazu gehören wie in Abbildung 13 dargestellt, die Werte die für die Manöversteuerung relevant sind und die Werte für das Modul Modell. Ebenso kann durch das ausführen der Parameterdatei das Simulink Modell geöffnet werden.
MATLAB GUI
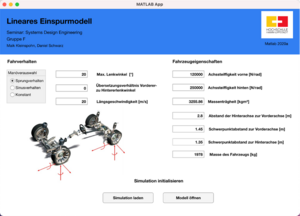
Die erstellte MATLAB GUI (Abbildung 14) ist eine Erweiterung der Parameterdatei. Dem Anwender wird es ermöglicht unter der Rubrik Fahrmanöver verschiedene Manöver auszuwählen. Ebenso kann der Lenkwinkel, das Übersetzungsverhältnis des vorderen- zu hinteren Lenkwinkels und die Längsgeschwindigkeit angepasst werden. Des Weiteren können die Fahrzeugeigenschaften Achssteifigkeiten, Massenträgheit, Abstände und Masse variiert werden. Unter der Rubrik Simulation initialisieren kann das Simulink Modell durch die GUI geöffnet und die Simulation geladen werden.
Fazit
Das lineare Einspurmodell ist ein komplexes Thema und erfordert weitreichende ingenieurswissenschaftliche Kenntnisse insbesondere in der Automobiltechnik. Durch die Aufgabe konnten vertiefte Fachkenntnisse in der Anwendung des V-Modells erlangt und bereits vorhandene Fähigkeiten aus vorherigen Modulen erweitert und angewendet werden. Insbesondere wurden die Softwarefähigkeiten durch die Anwendung von MATLAB Simulink weitestgehend gesteigert. Zusammenfassend lässt sich festhalten, dass die Erstellung des Lastenhefts mit besonderer Sorgfalt erstellt werden musste, da dieses Dokument die Basis der gesamten Arbeit bildet. Ebenfalls wurde festgestellt, dass die Erstellung der Komponentenspezifikation sich als schwierig herausstellte. Die Modellierung ist aufgrund der geforderten Simulink Kenntnisse und dem Umfang der benötigten Formeln sehr komplex. Jedoch konnten alle auftretenden Schwierigkeiten aufgrund der ausreichend gegebenen Zeit gelöst werden. Dem Anwender wird es ermöglicht, mithilfe des lineare Einspurmodells, jegliches lineare Fahrverhalten durch Anpassung der Fahrzeugeigenschaften und des Fahrverhaltens zu simulieren. Demzufolge konnte die Seminaraufgabe, das lineare Einspurmodell nach dem V-Modell zu konzipieren und zu modellieren, insgesamt erfolgreich abgeschlossen werden.
Literaturverzeichnis
→ zurück zum Hauptartikel: "Systems Design Engineering" - Seminaraufgabe SoSe 2021: Einspurmodell“