Stopplinienerkennung mit Hough-Transformation: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
Hinweise auf aktuelle Version und Artikel |
||
| (35 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
''' | '''Autoren:''' [[Benutzer:Kevin Hustedt| Kevin Hustedt]], [[Benutzer:Moritz Oberg| Moritz Oberg]] | ||
<span style="color:#FF0000">'''Hinweise:''' </span> | |||
* <span style="color:#FF0000"> Der zu dieser Beschreibung zugehörige Quelltext befindet sich nicht im Software-Ordner des Projekts. Stattdessen ist der Quelltext [https://svn.hshl.de/svn/MTR_SDE_Praktikum/trunk/Teams/OSE/OSE_Hustedt_Oberg/Testumgebung_Stopplinienerkennung hier] zu finden. </span> | |||
* <span style="color:#FF0000"> Eine Beschreibung der aktuellen Vorgehensweise von Spurerkennung und Stopplinienerkennung befindet sich auf der Wiki-Seite [https://wiki.hshl.de/wiki/index.php/OSE_Softwareumgebung OSE Softwareumgebung].</span> | |||
== Einleitung == | == Einleitung == | ||
| Zeile 6: | Zeile 11: | ||
== Lastenheft == | == Lastenheft == | ||
<gallery mode = "traditional" widths=700px heights=200px> | <gallery mode = "traditional" widths=700px heights=200px> | ||
File:REQ10.2340_Verhalten_an_Stopp-Kreuzungen.PNG|Abbildung 1: REQ.10.2340 Verhalten an Stopp-Kreuzungen | File:REQ10.2340_Verhalten_an_Stopp-Kreuzungen.PNG|Abbildung 1: REQ.10.2340 Verhalten an Stopp-Kreuzungen. | ||
</gallery> | </gallery> | ||
== Pflichtenheft == | == Pflichtenheft == | ||
<gallery mode = "traditional" widths=1000px heights=370px> | |||
File:Pflichtenheft_Stopplinienerkennung_Hustedt_Oberg.PNG|Abbildung 2: Ausschnitt aus dem Pflichtenheft. Pflichten zur Stopplinienerkennung. | |||
</gallery> | |||
== Programmablaufplan == | == Programmablaufplan == | ||
<gallery mode = "traditional" widths=400px heights=750px> | <gallery mode = "traditional" widths=400px heights=750px> | ||
File:PAP_Stopplinienerkennung_Houghline.PNG|Abbildung 3: Programmablaufplan der Stopplinienerkennung | File:PAP_Stopplinienerkennung_Houghline.PNG|Abbildung 3: Programmablaufplan der Stopplinienerkennung. | ||
File:PAP_WinkelLaengePruefen.PNG|Abbildung 4: Unterprogramm zum Überprüfen der Länge und des Winkels | File:PAP_WinkelLaengePruefen.PNG|Abbildung 4: Unterprogramm zum Überprüfen der Länge und des Winkels von allen relevanten Linien. | ||
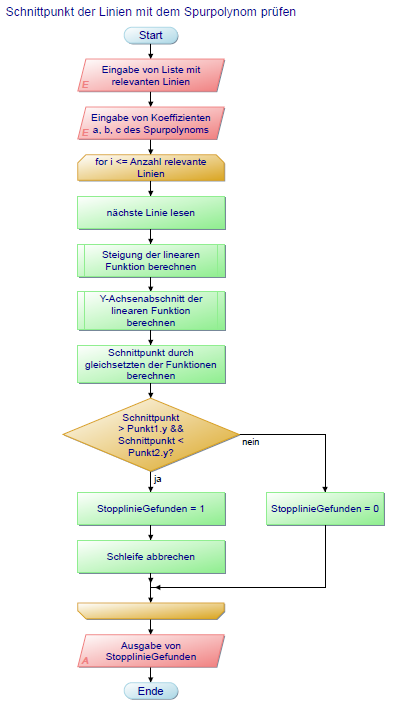
File:PAP_SchnittpunktPruefen.PNG|Abbildung 5: Unterprogramm zum Überprüfen des Schnittpunktes | File:PAP_SchnittpunktPruefen.PNG|Abbildung 5: Unterprogramm zum Überprüfen des Schnittpunktes von allen relevanten Linien. | ||
</gallery> | </gallery> | ||
| Zeile 22: | Zeile 30: | ||
=== Programmablauf === | === Programmablauf === | ||
Der Programmablauf der Stopplinienerkennung ist in Abbildung 3 zu sehen. Auf dem Auto wird in regelmäßigen Schritten ein neues Bild mit der Kamera aufgenommen. Das Bild der Kamera wird | Der Programmablauf der Stopplinienerkennung ist in Abbildung 3 zu sehen. Auf dem Auto wird in regelmäßigen Schritten ein neues Bild mit der Kamera aufgenommen. Im folgenden Abschnitt werden die einzelnen Schritte des Programmablaufes beschrieben. | ||
'''1. Eingabe''' | |||
Das Bild der Kamera (vgl. Abb. 6) wird zunächst in der Bildtransformation in ein Graustufenbild gewandelt und in die Vogelperspektive transformiert (vgl. Abb. 7). | |||
<gallery mode = "traditional" widths=400px heights=300px> | |||
File:Stopplinienerkennung_100cm.png|Abbildung 6: Bild von der Kamera vor der Transformation. | |||
File:stopplinienerkennung_100cm_vogelperspektive.PNG|Abbildung 7: Bild nach der Transformation. | |||
</gallery> | |||
Danach erfolgt in der '''[[OSE - Objekt - und Spurerkennung|Spurerkennung]]''' die Berechnung des Spurpolynoms. Das Spurpolynom beschreibt den Verlauf der Fahrbahn in dem aufgenommenen Bild. Das Spurpolynom ist ein Polynom 2. grades und hat folgende Form: <br> | |||
<br> | |||
<math>f(x) = ax^2 + bx + c</math> | |||
<br> | |||
Das in die Vogelperspektive transformierte Bild und die Koeffizienten a, b und c des Spurpolynoms, werden dann der Stopplinienerkennung als Funktionsparameter übergeben. | |||
'''2. Schnittstelle zurücksetzen''' | |||
Für die '''[[Datenübertragung zwischen PC und dSPACE Karte|Datenübertragung zwischen PC und dSPACE Karte]]''' wurde eine Datenstruktur angelegt. Die Refernez der Datenstruktur wird der Stopplinienerkennung übergeben. Die Datenstruktur beinhaltet unter anderem ein Bit, welches anzeigt das eine Stopplinie erkannt wurde und den Abstand zu der gefundenen Stopplinie. Beide Werte werden zu Beginn eines Programmdurchlaufes zurückgesetzt. | |||
'''3. Region of Interest erstellen''' | |||
In Abbildung 7 ist das Bild nach der Transformation zu sehen, welches der Stopplinienerkennung übergeben wird. In dem Bild kann man erkennen, dass nicht das gesamte Bild relevant für die Erkennung einer Stopplinie ist. Aus diesem Grund wird im weiteren Verlauf, nur ein Ausschnitt aus diesem Bild untersucht. Dazu wird mit Hilfe einer Funktion ein Ausschnitt aus dem Bild (Region of Interest) erstellt. Ein weiterer Vorteil ist die Verringerung der Programmdurchlaufzeit, da vom Algorithmus nur ein kleines Bild verarbeitet werden muss. Die Größe des Bildausschnittes kann über Parameter in der Stopplinienerkennung beliebig eingestellt werden. | |||
'''4. Linien im Bild finden''' | |||
Im nächsten Schritt werden in dem Bildausschnitt Linien gesucht. Für das Suchen der Linien wird die Hough Line Transformation verwendet. Die Hough Line Tranformation wird verwendet um gerade Linien in einem binären Bild zu finden. In diesem Fall wird die Funktion cv::HoughlineP() aus der Programmbibliothek OpenCV verwendet. Der Funktion wird dazu ein binäres Bild übergeben. Als Rückgabe erhält man eine Liste mit Linien. Die Linien werden durch jeweils zwei Punkten: P1(x,y) und P2(x,y) beschrieben, wobei die Punkte in kartesischen Koordinaten angegeben werden. | |||
'''5. Länge und Winkel der gefundenen Linien prüfen''' | |||
Um die Anzahl an Linie zu reduzieren, werden die gefundenen Linien hinsichtlich Länge und Winkel untersucht, damit nur Linien weiter verfolgt werden, die die Kriterien einer Stopplinie erfüllen. Dabei fallen zu kurze Linien raus und Linien die zum Beispiel senkrecht zum Fahrzeug stehen. Senkrechte Linien stammen zum Beispiel von einer Fahrbahnmarkierung. | |||
Eine Linie wird mit Hilfe von zwei Punkten beschreiben. Der Winkel in Grad einer Linie kann folgendermaßen berechnet werden: <br> | |||
<br> | |||
<math>Winkel = arctan(\frac{P2.x - P1.x}{P2.y - P1.y}) * \frac{180}{\pi}</math> | |||
<br> | |||
Die Länge einer Linie kann mit der folgenden Formel berechnet werden: <br> | |||
<br> | |||
<math>Laenge = \sqrt{(P2.x - P1.x)^2 + (P2.y - P1.y)^2}</math> | |||
<br> | |||
Alle Linien, welche die Kriterien erfüllen, werden gespeichert und weiter verarbeitet, alle anderen Linien werden ignoriert. | |||
Der Programmablauf dieser Funktion ist in Abbildung 4 zu sehen. | |||
'''6. Linien in das originale Bild transformieren''' | |||
Im nächsten Schritt werden die Punkte der relevanten Linien in das originale Bild zurück transformiert. Grund dafür ist die Berechnung des Schnittpunktes im darauffolgenden Schritt. Hier wird von jeder Linie der Schnittpunkt mit dem Spurpolynom berechnet und ausgewertet. Die Koeffizienten des Spurpolynoms sind allerdings für das originale Bild berechnet worden und die Linien wurden in dem Bildausschnitt gesucht. Um den Schnittpunkt richtig berechnen zu können, müssen die Linien in das originale Bild transformiert werden. | |||
'''7. Schnittpunkt der Linien mit dem Spurpolynom prüfen''' | |||
Das Kriterium von Länge und Winkel, um eine Linie als Stopplinie zu identifizieren, reicht nicht aus. Grund dafür ist, dass im Bild Linien vorkommen können, welche die Kriterien erfüllen, aber keine Stopplinie sind. | |||
Aus diesem Grund werden die gefundenen Linien zusätzlich hinsichtlich des Schnittpunkts mit dem Spurpolynom untersucht. Der Programmablauf dieser Funktion ist in Abbildung 5 zu sehen. | |||
Dazu werden die beiden Punkte einer Linie genutzt, um eine lineare Funktion zu berechnen. | |||
Die lineare Funktion hat dann folgende Form: <br> | |||
<br> | |||
<math>f(x) = mx + d</math> | |||
<br> | |||
Dabei ist m die Steigung der linearen Funktion und d der y-Achsenabschnitt der Funktion. | |||
Durch gleichsetzen der linearen Funktion und der Funktion des Spurpolynoms, erhält man den Schnittpunkt: <br> | |||
<br> | |||
<math>ax^2 + bx + c = mx + d</math> | |||
<br> | |||
Nach x umgestellt sieht die Gleichung folgendermaßen aus: <br> | |||
<br> | |||
<math>x = \frac{\sqrt{-4ac+4ad+b^2-2bm+m^2}-b+m}{2a} </math> | |||
<br> | |||
Ein Schnittpunkt der Linie mit dem Spurpolynom liegt dann vor, wenn die Lösung der Gleichung nicht komplex ist und der Schnittpunkt zwischen den beiden Endpunkten der Linie liegt: Schnittpunkt > P1.y und Schnittpunkt < P2.y | |||
Wenn die Bedingungen erfüllt sind, dann wird die Suche abgebrochen und das entsprechende Bit gesetzt, dass eine Stopplinie gefunden wurde. | |||
Wenn die Linie die Bedingungen nicht erfüllt, dann wird die nächste Linie untersucht. | |||
'''8. if-Anweisung und Abstand berechnen''' | |||
Wenn eine Stopplinie gefunden wurde, dann wird der Abstand zu dieser Linie berechnet. Dazu wird die Anzahl an Pixeln gezählt, die sich zwischen dem Auto und der Linie befinden. Der Abstand in Pixel dividiert durch den Kameraparameter (Pixel/Meter) ergibt dann den Abstand zum Auto in Meter. Der Abstandswert wird schlussendlich in der Datenstruktur der Kommunikationsschnittstelle geschrieben und das entsprechende Bit gesetzt. | |||
Wenn keine Stopplinie gefunden wurde, dann bleibt die Schnittstelle zurückgesetzt. | |||
'''9. Ausgabe''' | |||
Von der Funktion wird der Abstand der Stopplinie sowie das Bit, ob eine Stopplinie gefunden wurde, zurückgegeben. | |||
<br> | |||
===Erläuterung=== | |||
Während der einzelnen Programmabschnitte kommt es zu einem Wechsel der Koordinatensysteme. Das Koordinatensystem wechselt von dem transformierten Bild auf den Ausschnitt der ROI. Im Verlauf der weiteren Datenverarbeitung werden die X und Y Achsen vertauscht. Nachdem der Bereich der ROI in das originale Bild der Vogelperspektive zurücktransformiert wurde, kann der Schnittpunkt mit zwischen der gefundenen Linie und dem Spurpolynom bestimmt werden. Die folgende Abbildung dient zur besseren Verständlichkeit des Programms und zeigt die verschiedenen Koordinatensysteme. Der Koordinatenursprung ist als blauer Punkt eingezeichnet. Die grünen Pfeile zeigen in die positive Richtung der jeweiligen Achse. | |||
<gallery mode = "traditional" widths=400px heights=300px> | |||
File:Skizze_Koordinatensysteme.png|Abbildung 8: Skizze zur erläuterung der Koordinatentransformationen. | |||
</gallery> | |||
== Komponententest == | |||
[[Datei:Unittest_Stopplinienerkennung_Bild250.PNG|thumb|rigth|400px|Abbildung 8: Bild250 ohne Stopplinie.]] | |||
[[Datei:Unittest_Stopplinienerkennung_Bild440.PNG|thumb|rigth|400px|Abbildung 9: Bild440 mit Stopplinie.]] | |||
Für den Test der Stopplinienerkennung wurden eine Testumgebung erstellt, die alle notwendigen Funktionen ausführt. | |||
Für den Test wurden verschiedene Bilder auf denen eine Stopplinie zu sehen ist und welche auf denen keine zu sehen ist, mit der Kamera des Fahrzeugs aufgenommen. Die Bilder wurden dann mit Hilfe der Testumgebung eingelesen, transformiert und der Stopplinienerkennung übergeben. | |||
In Abbildung 8 und 9 ist jeweils ein Testbild zu sehen, welches für den Test verwendet wurde. In Rot wurde jeweils das berechnete Spurpolynom eingezeichnet. Die Linie wurde nur im relevanten Bildausschnitt eingezeichnet. In Abbildung 9 ist zusätzlich in grün, die gefundene Stopplinie eingezeichnet. | |||
Die Ergebnisse des Tests sind in nachfolgender Tabelle zu sehen. | |||
{| class="mw-datatable" | |||
! style="font-weight: bold;" | ID | |||
! style="font-weight: bold;" | Testfallbeschreibung | |||
! style="font-weight: bold;" | Eingang | |||
! style="font-weight: bold;" | Erwartetes Ergebnis | |||
! style="font-weight: bold;" | Testergebnis | |||
! style="font-weight: bold;" | Testperson | |||
! style="font-weight: bold;" | Datum | |||
|- | |||
| 1 | |||
| Testbild mit Kurve. Keine Stopplinie im Bild zu sehen. | |||
| Bild350.png | |||
| Keine Stopplinie gefunden | |||
| i.O. | |||
| Hustedt | |||
| 21.01.2021 | |||
|- | |||
| 2 | |||
| Testbild mit gerader Strecke. Keine Stopplinie im Bild zu sehen. | |||
| Bild25.png | |||
| Keine Stopplinie gefunden | |||
| i.O. | |||
| Hustedt | |||
| 21.01.2021 | |||
|- | |||
| 3 | |||
| Testbild mit Stoppkreuzung. Keine Stopplinie im Bild zu sehen. | |||
| Bild500.png | |||
| Keine Stopplinie gefunden | |||
| i.O. | |||
| Hustedt | |||
| 21.01.2021 | |||
|- | |||
| 4 | |||
| Testbild mit Hindernissen im Hintergrund. Keine Stopplinie im Bild zu sehen. | |||
| Bild300.png | |||
| Keine Stopplinie gefunden | |||
| i.O. | |||
| Hustedt | |||
| 21.01.2021 | |||
|- | |||
| 5 | |||
| Testbild vor einer Kurve. Keine Stopplinie im Bild zu sehen. | |||
| Bild250.png | |||
| Keine Stopplinie gefunden | |||
| i.O. | |||
| Hustedt | |||
| 21.01.2021 | |||
|- | |||
| 6 | |||
| Testbild kurz nach einer Stopplinie. Keine Stopplinie im Bild zu sehen. | |||
| Bild452.png | |||
| Keine Stopplinie gefunden | |||
| i.O. | |||
| Hustedt | |||
| 21.01.2021 | |||
|- | |||
| 7 | |||
| Testbild kurz vor einer Stopplinie. Stopplinie im Bild zu sehen. | |||
| Bild450.png | |||
| Stopplinie gefunden | |||
| i.O. | |||
| Hustedt | |||
| 21.01.2021 | |||
|- | |||
| 8 | |||
| Testbild gerade vor einer Stopplinie. Stopplinie im Bild zu sehen. | |||
| Bild440.png | |||
| Stopplinie gefunden | |||
| i.O. | |||
| Hustedt | |||
| 21.01.2021 | |||
|- | |||
| 9 | |||
| Testbild schräg vor einer Stopplinie. Stopplinie im Bild zu sehen. | |||
| Bild422.png | |||
| Stopplinie gefunden | |||
| i.O. | |||
| Hustedt | |||
| 21.01.2021 | |||
|- | |||
|} | |||
== | Für einen zweiten Test wurden verschiedene Bilder mit unterschiedlichen Abständen zu einer Stopplinie aufgenommen, um die Berechnung der Entfernung zur Stopplinie zu testen. Der Abstand wurde für die Auswertung des Tests in der Konsole ausgegeben. Die Testfälle können der nachfolgenden Tabelle entnommen werden. | ||
{| class="mw-datatable" | |||
! style="font-weight: bold;" | ID | |||
! style="font-weight: bold;" | Testfallbeschreibung | |||
! style="font-weight: bold;" | Eingang | |||
! style="font-weight: bold;" | Erwartetes Ergebnis | |||
! style="font-weight: bold;" | Testergebnis | |||
! style="font-weight: bold;" | Testperson | |||
! style="font-weight: bold;" | Datum | |||
|- | |||
| 1 | |||
| Testbild mit einem Abstand von 20 cm zur Stopplinie übergeben. | |||
| 20cm.png | |||
| Stopplinie gefunden | |||
| i.O. | |||
| Hustedt | |||
| 21.01.2021 | |||
|- | |||
| 2 | |||
| Testbild mit einem Abstand von 40 cm zur Stopplinie übergeben. | |||
| 40cm.png | |||
| Stopplinie gefunden | |||
| i.O. | |||
| Hustedt | |||
| 21.01.2021 | |||
|- | |||
| 3 | |||
| Testbild mit einem Abstand von 60 cm zur Stopplinie übergeben. | |||
| 60cm.png | |||
| Stopplinie gefunden | |||
| i.O. | |||
| Hustedt | |||
| 21.01.2021 | |||
|- | |||
| 4 | |||
| Testbild mit einem Abstand von 80 cm zur Stopplinie übergeben. | |||
| 80cm.png | |||
| Stopplinie gefunden | |||
| i.O. | |||
| Hustedt | |||
| 21.01.2021 | |||
|- | |||
| 5 | |||
| Testbild mit einem Abstand von 100 cm zur Stopplinie übergeben. | |||
| 100cm.png | |||
| Stopplinie gefunden | |||
| i.O. | |||
| Hustedt | |||
| 21.01.2021 | |||
|- | |||
| 6 | |||
| Testbild mit einem Abstand von 20 cm zur Stopplinie übergeben. | |||
| 20cm.png | |||
| Abstand 20 cm | |||
| 19.63 cm | |||
| Hustedt | |||
| 21.01.2021 | |||
|- | |||
| 7 | |||
| Testbild mit einem Abstand von 40 cm zur Stopplinie übergeben. | |||
| 40cm.png | |||
| Abstand 40 cm | |||
| 43.63 cm | |||
| Hustedt | |||
| 21.01.2021 | |||
|- | |||
| 8 | |||
| Testbild mit einem Abstand von 60 cm zur Stopplinie übergeben. | |||
| 60cm.png | |||
| Abstand 60 cm | |||
| 60.36 cm | |||
| Hustedt | |||
| 21.01.2021 | |||
|- | |||
| 9 | |||
| Testbild mit einem Abstand von 80 cm zur Stopplinie übergeben. | |||
| 80cm.png | |||
| Abstand 80 cm | |||
| 88.73 cm | |||
| Hustedt | |||
| 21.01.2021 | |||
|- | |||
| 10 | |||
| Testbild mit einem Abstand von 100 cm zur Stopplinie übergeben. | |||
| 100cm.png | |||
| Abstand 100 cm | |||
| 101.82 cm | |||
| Hustedt | |||
| 21.01.2021 | |||
|- | |||
|} | |||
== | == Video der Stopplinienerkennung == | ||
Das Video zeigt das Ergebnis der implementierten Stopplinienerkennung. In dem Video wird die transformierte Perspektive angezeigt. Zusätzlich zeigt eine rote Linie den Verlauf des Spurpolynoms an und eine grüne Linie die gefundene Stopplinie. In der linken oberen Ecke des Videos wird zusätzlich angezeigt, ob eine Stopplinie gefunden wurde oder nicht. Außerdem wird der berechnete Abstand zur Stopplinie angezeigt. | |||
<br> | |||
<br> | |||
[[File:video_stopplinienerkennung_opencv.webm|start=0|end=46|Video Stopplinienerkennung]] | |||
== Ausblick == | == Zusammenfassung und Ausblick == | ||
Die Stopplinienerkennung für das Fahrzeug konnte erfolgreich umgesetzt werden. Die Stopplinienerkennung wurde in der Programmiersprache C/C++ umgesetzt und mit Hilfe der Programmbibliothek OpenCV. Für die Erkennung wird ein binäres Bild, welches zuvor in die Vogelperspektive transformiert wurde, verwendet. Das Bild wird mit der Kamera des Fahrzeugs aufgenommen. In dem Bild werden dann mit Hilfe der Funktion cv::HoughlineP gerade Linien gesucht. Die gefundenen Linien werden hinsichtlich Länge und Winkel untersucht. Zusätzlich wird der Schnittpunkt mit dem berechneten Spurpolynom berechnet und als weiteres Kriterium für eine Stopplinie hinzugezogen. Stimmen Länge, Winkel und der Schnittpunkt mit den gegebenen Kriterien überein, handelt es sich um eine Stopplinie. Wenn eine Stopplinie gefunden wurde, dann wird der Abstand zu dieser Linie berechnet. Die Informationen werden über eine Schnittstelle zur dSPACE Karte gesendet. | |||
Die Stopplinienerkennung konnte erfolgreich umgesetzt und mit Testbildern und Testvideos getestet werden. Der Test der Integration konnte aufgrund von fehlenden Funktionalitäten anderer Module des Projektes und aufgrund von geschlossenen Laboren noch nicht umgesetzt werden. | |||
<br> | |||
<br> | |||
<hr> | |||
→ zurück zum Hauptartikel: [[Praktikum_SDE|Praktikum SDE]] <br> | |||
→ zurück zum Hauptartikel: [[OSE_-_Objekt_-_und_Spurerkennung|OSE Objekt - und Spurerkennung]] | |||
Aktuelle Version vom 27. September 2022, 12:52 Uhr
Autoren: Kevin Hustedt, Moritz Oberg
Hinweise:
- Der zu dieser Beschreibung zugehörige Quelltext befindet sich nicht im Software-Ordner des Projekts. Stattdessen ist der Quelltext hier zu finden.
- Eine Beschreibung der aktuellen Vorgehensweise von Spurerkennung und Stopplinienerkennung befindet sich auf der Wiki-Seite OSE Softwareumgebung.
Einleitung
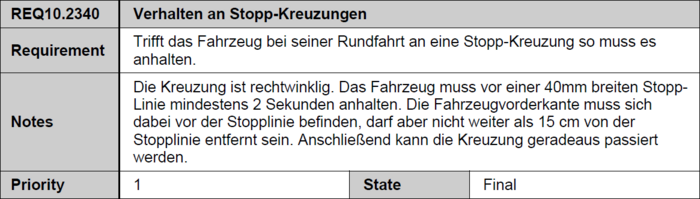
Im Praktikum des Studienschwerpunkts Systems Designe Engineering des Studiengangs Mechatronik, wird ein autonom fahrendes Modellauto entwickelt. Dieses Auto soll auf einem Rundkurs fahren, der unteranderem Kreuzungen mit Stopplinien beinhaltet. Das Auto soll automatisch an diesen Stopplinien halten. Für das Stoppen muss das Auto die Stopplinien über die eingebaute Kamera erkennen und den Abstand fortlaufend berechnen. Dies geht aus dem Lastenheft des Praktikums hervor (vgl. Abb. 1).
Lastenheft
-
Abbildung 1: REQ.10.2340 Verhalten an Stopp-Kreuzungen.
Pflichtenheft
-
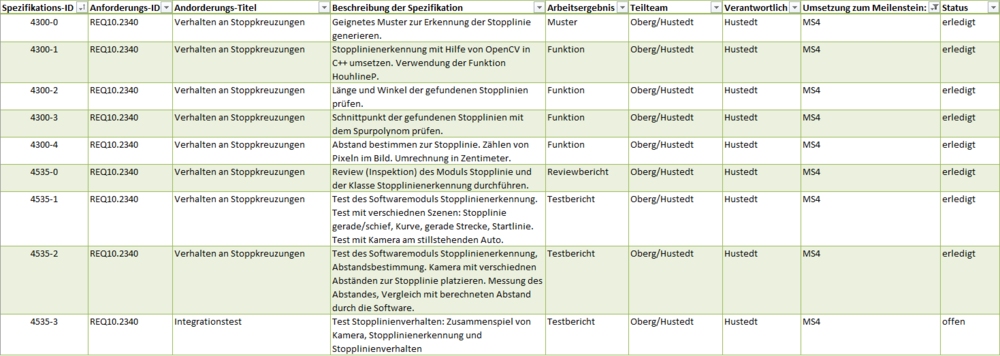
Abbildung 2: Ausschnitt aus dem Pflichtenheft. Pflichten zur Stopplinienerkennung.
Programmablaufplan
-
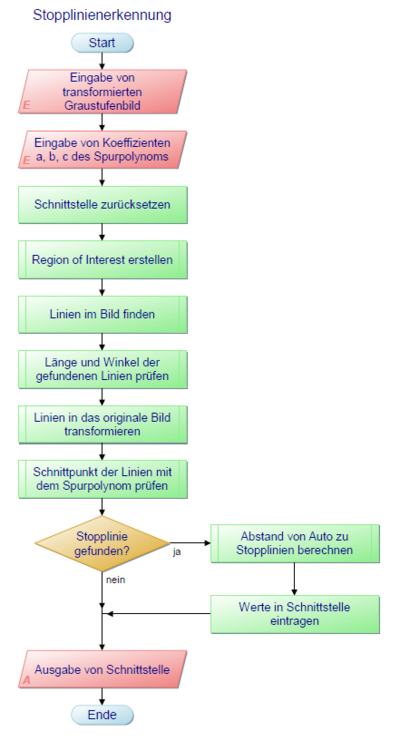
Abbildung 3: Programmablaufplan der Stopplinienerkennung.
-
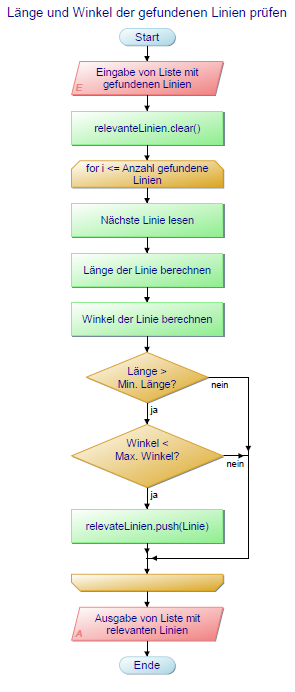
Abbildung 4: Unterprogramm zum Überprüfen der Länge und des Winkels von allen relevanten Linien.
-
Abbildung 5: Unterprogramm zum Überprüfen des Schnittpunktes von allen relevanten Linien.
Programm
Die Stopplinienerkennung wurde in der Programmiersprache C/C++ umgesetzt. Als Entwicklungsumgebung diente Visual Studio 2019. Es wurden Funktionen und Datentypen aus der Programmbibliothek OpenCV verwendet. Die Bibliothek muss für die Verwendung in die Entwicklungsumgebung Visual Studio eingebunden werden, eine ausführliche Anleitung für das Einbinden ist hier zu finden: Einrichten von OpenCV
Programmablauf
Der Programmablauf der Stopplinienerkennung ist in Abbildung 3 zu sehen. Auf dem Auto wird in regelmäßigen Schritten ein neues Bild mit der Kamera aufgenommen. Im folgenden Abschnitt werden die einzelnen Schritte des Programmablaufes beschrieben.
1. Eingabe
Das Bild der Kamera (vgl. Abb. 6) wird zunächst in der Bildtransformation in ein Graustufenbild gewandelt und in die Vogelperspektive transformiert (vgl. Abb. 7).
-
Abbildung 6: Bild von der Kamera vor der Transformation.
-
Abbildung 7: Bild nach der Transformation.
Danach erfolgt in der Spurerkennung die Berechnung des Spurpolynoms. Das Spurpolynom beschreibt den Verlauf der Fahrbahn in dem aufgenommenen Bild. Das Spurpolynom ist ein Polynom 2. grades und hat folgende Form:
Das in die Vogelperspektive transformierte Bild und die Koeffizienten a, b und c des Spurpolynoms, werden dann der Stopplinienerkennung als Funktionsparameter übergeben.
2. Schnittstelle zurücksetzen
Für die Datenübertragung zwischen PC und dSPACE Karte wurde eine Datenstruktur angelegt. Die Refernez der Datenstruktur wird der Stopplinienerkennung übergeben. Die Datenstruktur beinhaltet unter anderem ein Bit, welches anzeigt das eine Stopplinie erkannt wurde und den Abstand zu der gefundenen Stopplinie. Beide Werte werden zu Beginn eines Programmdurchlaufes zurückgesetzt.
3. Region of Interest erstellen
In Abbildung 7 ist das Bild nach der Transformation zu sehen, welches der Stopplinienerkennung übergeben wird. In dem Bild kann man erkennen, dass nicht das gesamte Bild relevant für die Erkennung einer Stopplinie ist. Aus diesem Grund wird im weiteren Verlauf, nur ein Ausschnitt aus diesem Bild untersucht. Dazu wird mit Hilfe einer Funktion ein Ausschnitt aus dem Bild (Region of Interest) erstellt. Ein weiterer Vorteil ist die Verringerung der Programmdurchlaufzeit, da vom Algorithmus nur ein kleines Bild verarbeitet werden muss. Die Größe des Bildausschnittes kann über Parameter in der Stopplinienerkennung beliebig eingestellt werden.
4. Linien im Bild finden
Im nächsten Schritt werden in dem Bildausschnitt Linien gesucht. Für das Suchen der Linien wird die Hough Line Transformation verwendet. Die Hough Line Tranformation wird verwendet um gerade Linien in einem binären Bild zu finden. In diesem Fall wird die Funktion cv::HoughlineP() aus der Programmbibliothek OpenCV verwendet. Der Funktion wird dazu ein binäres Bild übergeben. Als Rückgabe erhält man eine Liste mit Linien. Die Linien werden durch jeweils zwei Punkten: P1(x,y) und P2(x,y) beschrieben, wobei die Punkte in kartesischen Koordinaten angegeben werden.
5. Länge und Winkel der gefundenen Linien prüfen
Um die Anzahl an Linie zu reduzieren, werden die gefundenen Linien hinsichtlich Länge und Winkel untersucht, damit nur Linien weiter verfolgt werden, die die Kriterien einer Stopplinie erfüllen. Dabei fallen zu kurze Linien raus und Linien die zum Beispiel senkrecht zum Fahrzeug stehen. Senkrechte Linien stammen zum Beispiel von einer Fahrbahnmarkierung.
Eine Linie wird mit Hilfe von zwei Punkten beschreiben. Der Winkel in Grad einer Linie kann folgendermaßen berechnet werden:
Die Länge einer Linie kann mit der folgenden Formel berechnet werden:
Alle Linien, welche die Kriterien erfüllen, werden gespeichert und weiter verarbeitet, alle anderen Linien werden ignoriert.
Der Programmablauf dieser Funktion ist in Abbildung 4 zu sehen.
6. Linien in das originale Bild transformieren
Im nächsten Schritt werden die Punkte der relevanten Linien in das originale Bild zurück transformiert. Grund dafür ist die Berechnung des Schnittpunktes im darauffolgenden Schritt. Hier wird von jeder Linie der Schnittpunkt mit dem Spurpolynom berechnet und ausgewertet. Die Koeffizienten des Spurpolynoms sind allerdings für das originale Bild berechnet worden und die Linien wurden in dem Bildausschnitt gesucht. Um den Schnittpunkt richtig berechnen zu können, müssen die Linien in das originale Bild transformiert werden.
7. Schnittpunkt der Linien mit dem Spurpolynom prüfen
Das Kriterium von Länge und Winkel, um eine Linie als Stopplinie zu identifizieren, reicht nicht aus. Grund dafür ist, dass im Bild Linien vorkommen können, welche die Kriterien erfüllen, aber keine Stopplinie sind. Aus diesem Grund werden die gefundenen Linien zusätzlich hinsichtlich des Schnittpunkts mit dem Spurpolynom untersucht. Der Programmablauf dieser Funktion ist in Abbildung 5 zu sehen.
Dazu werden die beiden Punkte einer Linie genutzt, um eine lineare Funktion zu berechnen.
Die lineare Funktion hat dann folgende Form:
Dabei ist m die Steigung der linearen Funktion und d der y-Achsenabschnitt der Funktion.
Durch gleichsetzen der linearen Funktion und der Funktion des Spurpolynoms, erhält man den Schnittpunkt:
Nach x umgestellt sieht die Gleichung folgendermaßen aus:
Ein Schnittpunkt der Linie mit dem Spurpolynom liegt dann vor, wenn die Lösung der Gleichung nicht komplex ist und der Schnittpunkt zwischen den beiden Endpunkten der Linie liegt: Schnittpunkt > P1.y und Schnittpunkt < P2.y
Wenn die Bedingungen erfüllt sind, dann wird die Suche abgebrochen und das entsprechende Bit gesetzt, dass eine Stopplinie gefunden wurde.
Wenn die Linie die Bedingungen nicht erfüllt, dann wird die nächste Linie untersucht.
8. if-Anweisung und Abstand berechnen
Wenn eine Stopplinie gefunden wurde, dann wird der Abstand zu dieser Linie berechnet. Dazu wird die Anzahl an Pixeln gezählt, die sich zwischen dem Auto und der Linie befinden. Der Abstand in Pixel dividiert durch den Kameraparameter (Pixel/Meter) ergibt dann den Abstand zum Auto in Meter. Der Abstandswert wird schlussendlich in der Datenstruktur der Kommunikationsschnittstelle geschrieben und das entsprechende Bit gesetzt. Wenn keine Stopplinie gefunden wurde, dann bleibt die Schnittstelle zurückgesetzt.
9. Ausgabe
Von der Funktion wird der Abstand der Stopplinie sowie das Bit, ob eine Stopplinie gefunden wurde, zurückgegeben.
Erläuterung
Während der einzelnen Programmabschnitte kommt es zu einem Wechsel der Koordinatensysteme. Das Koordinatensystem wechselt von dem transformierten Bild auf den Ausschnitt der ROI. Im Verlauf der weiteren Datenverarbeitung werden die X und Y Achsen vertauscht. Nachdem der Bereich der ROI in das originale Bild der Vogelperspektive zurücktransformiert wurde, kann der Schnittpunkt mit zwischen der gefundenen Linie und dem Spurpolynom bestimmt werden. Die folgende Abbildung dient zur besseren Verständlichkeit des Programms und zeigt die verschiedenen Koordinatensysteme. Der Koordinatenursprung ist als blauer Punkt eingezeichnet. Die grünen Pfeile zeigen in die positive Richtung der jeweiligen Achse.
-
Abbildung 8: Skizze zur erläuterung der Koordinatentransformationen.
Komponententest

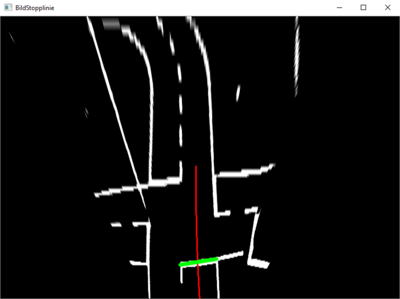
Für den Test der Stopplinienerkennung wurden eine Testumgebung erstellt, die alle notwendigen Funktionen ausführt. Für den Test wurden verschiedene Bilder auf denen eine Stopplinie zu sehen ist und welche auf denen keine zu sehen ist, mit der Kamera des Fahrzeugs aufgenommen. Die Bilder wurden dann mit Hilfe der Testumgebung eingelesen, transformiert und der Stopplinienerkennung übergeben.
In Abbildung 8 und 9 ist jeweils ein Testbild zu sehen, welches für den Test verwendet wurde. In Rot wurde jeweils das berechnete Spurpolynom eingezeichnet. Die Linie wurde nur im relevanten Bildausschnitt eingezeichnet. In Abbildung 9 ist zusätzlich in grün, die gefundene Stopplinie eingezeichnet.
Die Ergebnisse des Tests sind in nachfolgender Tabelle zu sehen.
| ID | Testfallbeschreibung | Eingang | Erwartetes Ergebnis | Testergebnis | Testperson | Datum |
|---|---|---|---|---|---|---|
| 1 | Testbild mit Kurve. Keine Stopplinie im Bild zu sehen. | Bild350.png | Keine Stopplinie gefunden | i.O. | Hustedt | 21.01.2021 |
| 2 | Testbild mit gerader Strecke. Keine Stopplinie im Bild zu sehen. | Bild25.png | Keine Stopplinie gefunden | i.O. | Hustedt | 21.01.2021 |
| 3 | Testbild mit Stoppkreuzung. Keine Stopplinie im Bild zu sehen. | Bild500.png | Keine Stopplinie gefunden | i.O. | Hustedt | 21.01.2021 |
| 4 | Testbild mit Hindernissen im Hintergrund. Keine Stopplinie im Bild zu sehen. | Bild300.png | Keine Stopplinie gefunden | i.O. | Hustedt | 21.01.2021 |
| 5 | Testbild vor einer Kurve. Keine Stopplinie im Bild zu sehen. | Bild250.png | Keine Stopplinie gefunden | i.O. | Hustedt | 21.01.2021 |
| 6 | Testbild kurz nach einer Stopplinie. Keine Stopplinie im Bild zu sehen. | Bild452.png | Keine Stopplinie gefunden | i.O. | Hustedt | 21.01.2021 |
| 7 | Testbild kurz vor einer Stopplinie. Stopplinie im Bild zu sehen. | Bild450.png | Stopplinie gefunden | i.O. | Hustedt | 21.01.2021 |
| 8 | Testbild gerade vor einer Stopplinie. Stopplinie im Bild zu sehen. | Bild440.png | Stopplinie gefunden | i.O. | Hustedt | 21.01.2021 |
| 9 | Testbild schräg vor einer Stopplinie. Stopplinie im Bild zu sehen. | Bild422.png | Stopplinie gefunden | i.O. | Hustedt | 21.01.2021 |
Für einen zweiten Test wurden verschiedene Bilder mit unterschiedlichen Abständen zu einer Stopplinie aufgenommen, um die Berechnung der Entfernung zur Stopplinie zu testen. Der Abstand wurde für die Auswertung des Tests in der Konsole ausgegeben. Die Testfälle können der nachfolgenden Tabelle entnommen werden.
| ID | Testfallbeschreibung | Eingang | Erwartetes Ergebnis | Testergebnis | Testperson | Datum |
|---|---|---|---|---|---|---|
| 1 | Testbild mit einem Abstand von 20 cm zur Stopplinie übergeben. | 20cm.png | Stopplinie gefunden | i.O. | Hustedt | 21.01.2021 |
| 2 | Testbild mit einem Abstand von 40 cm zur Stopplinie übergeben. | 40cm.png | Stopplinie gefunden | i.O. | Hustedt | 21.01.2021 |
| 3 | Testbild mit einem Abstand von 60 cm zur Stopplinie übergeben. | 60cm.png | Stopplinie gefunden | i.O. | Hustedt | 21.01.2021 |
| 4 | Testbild mit einem Abstand von 80 cm zur Stopplinie übergeben. | 80cm.png | Stopplinie gefunden | i.O. | Hustedt | 21.01.2021 |
| 5 | Testbild mit einem Abstand von 100 cm zur Stopplinie übergeben. | 100cm.png | Stopplinie gefunden | i.O. | Hustedt | 21.01.2021 |
| 6 | Testbild mit einem Abstand von 20 cm zur Stopplinie übergeben. | 20cm.png | Abstand 20 cm | 19.63 cm | Hustedt | 21.01.2021 |
| 7 | Testbild mit einem Abstand von 40 cm zur Stopplinie übergeben. | 40cm.png | Abstand 40 cm | 43.63 cm | Hustedt | 21.01.2021 |
| 8 | Testbild mit einem Abstand von 60 cm zur Stopplinie übergeben. | 60cm.png | Abstand 60 cm | 60.36 cm | Hustedt | 21.01.2021 |
| 9 | Testbild mit einem Abstand von 80 cm zur Stopplinie übergeben. | 80cm.png | Abstand 80 cm | 88.73 cm | Hustedt | 21.01.2021 |
| 10 | Testbild mit einem Abstand von 100 cm zur Stopplinie übergeben. | 100cm.png | Abstand 100 cm | 101.82 cm | Hustedt | 21.01.2021 |
Video der Stopplinienerkennung
Das Video zeigt das Ergebnis der implementierten Stopplinienerkennung. In dem Video wird die transformierte Perspektive angezeigt. Zusätzlich zeigt eine rote Linie den Verlauf des Spurpolynoms an und eine grüne Linie die gefundene Stopplinie. In der linken oberen Ecke des Videos wird zusätzlich angezeigt, ob eine Stopplinie gefunden wurde oder nicht. Außerdem wird der berechnete Abstand zur Stopplinie angezeigt.
Zusammenfassung und Ausblick
Die Stopplinienerkennung für das Fahrzeug konnte erfolgreich umgesetzt werden. Die Stopplinienerkennung wurde in der Programmiersprache C/C++ umgesetzt und mit Hilfe der Programmbibliothek OpenCV. Für die Erkennung wird ein binäres Bild, welches zuvor in die Vogelperspektive transformiert wurde, verwendet. Das Bild wird mit der Kamera des Fahrzeugs aufgenommen. In dem Bild werden dann mit Hilfe der Funktion cv::HoughlineP gerade Linien gesucht. Die gefundenen Linien werden hinsichtlich Länge und Winkel untersucht. Zusätzlich wird der Schnittpunkt mit dem berechneten Spurpolynom berechnet und als weiteres Kriterium für eine Stopplinie hinzugezogen. Stimmen Länge, Winkel und der Schnittpunkt mit den gegebenen Kriterien überein, handelt es sich um eine Stopplinie. Wenn eine Stopplinie gefunden wurde, dann wird der Abstand zu dieser Linie berechnet. Die Informationen werden über eine Schnittstelle zur dSPACE Karte gesendet.
Die Stopplinienerkennung konnte erfolgreich umgesetzt und mit Testbildern und Testvideos getestet werden. Der Test der Integration konnte aufgrund von fehlenden Funktionalitäten anderer Module des Projektes und aufgrund von geschlossenen Laboren noch nicht umgesetzt werden.
→ zurück zum Hauptartikel: Praktikum SDE
→ zurück zum Hauptartikel: OSE Objekt - und Spurerkennung