AlphaBot: Motoren und Inkrementalgeber: Unterschied zwischen den Versionen
| (26 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 7: | Zeile 7: | ||
== Inhalt == | == Inhalt == | ||
* Ansteurung der Motoren | |||
* Auslesen der Lichtschranken via Interrupt | |||
* Berechnung der gefahrenen Strecke | |||
* Fahrt einer definierten Strecke und Figur. | |||
* Berechnung des Kurswinkels aus diffenentieller Odometrie | |||
== Lernziele== | == Lernziele== | ||
Nach Durchführung dieser Lektion können Sie | Nach Durchführung dieser Lektion können Sie | ||
* die Fahrstrecke des linken und rechten Rades aus den Lichtschrankensignale berechnen. | |||
* eine definierte Strecke und Figur fahren. | |||
* die Position und Lage eines mobilen Roboters mittels diffenentieller Odometrie schätzen. | |||
== Versuchsdurchführung == | == Versuchsdurchführung == | ||
| Zeile 18: | Zeile 25: | ||
# Lassen Sie als Test beide Motoren langsam vorwärts drehen. | # Lassen Sie als Test beide Motoren langsam vorwärts drehen. | ||
# Flankenwechsel von <code>CNTL/CNTR</code> sollen einen [https://wiki.hshl.de/wiki/index.php/Arduino:_Interrupts Interrupt] auslösen. | # Flankenwechsel von <code>CNTL/CNTR</code> sollen einen [https://wiki.hshl.de/wiki/index.php/Arduino:_Interrupts Interrupt] auslösen. | ||
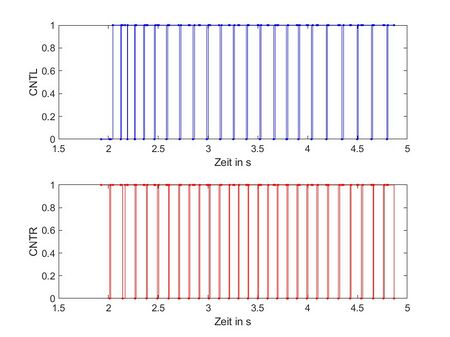
# Stellen Sie beide Lichtschrankenzustände <code>CNTL/CNTR</code> über der Zeit in MATLAB<sup>®</sup> dar. | # Stellen Sie beide Lichtschrankenzustände <code>CNTL/CNTR</code> über der Zeit in MATLAB<sup>®</sup> dar (vgl. Abb. 2). | ||
'''Lernzielkontrollfragen:''' | '''Lernzielkontrollfragen:''' | ||
| Zeile 26: | Zeile 33: | ||
* An welchen Ports sind die linke und rechte Lichtschranke angeschlossen? | * An welchen Ports sind die linke und rechte Lichtschranke angeschlossen? | ||
* Welche IO-Pins sind beim Arduino Uno interruptfähig? | * Welche IO-Pins sind beim Arduino Uno interruptfähig? | ||
* Wie | * Wie entscheidet die Lichtschranke zwischen Vorwärts- oder Rückwärtsdrehung? | ||
* Wieviele Flanken erhalten Sie für eine Radumdrehung? | * Wieviele Flanken erhalten Sie für eine Radumdrehung? | ||
'''Arbeitsergebnisse:''' <code>testeLichtschranke.ino</code>, <code>testeLichtschranke.m</code> | '''Arbeitsergebnisse:''' <code>testeLichtschranke.ino</code>, <code>testeLichtschranke.m, leseArduinoDaten.m</code> | ||
{| role="presentation" class="wikitable mw-collapsible mw-collapsed" | {| role="presentation" class="wikitable mw-collapsible mw-collapsed" | ||
| Zeile 38: | Zeile 45: | ||
| Nur die IO-Pins D2 und D3 sind beim Arduino Uno interruptfähig. | | Nur die IO-Pins D2 und D3 sind beim Arduino Uno interruptfähig. | ||
|- | |- | ||
| Legen Sie für eine langsame Raddrehung keine Akkus ein. | | Entfernen Sie die Multisensorerweiterung. | ||
|- | |||
| Legen Sie für eine langsame Raddrehung keine Akkus ein. Manche USB-Ports sind zu schwach um die Motoren zu betreiben. Dann müssen Sie die Akkus nutzen. | |||
|} | |} | ||
{| role="presentation" class="wikitable mw-collapsible mw-collapsed" | {| role="presentation" class="wikitable mw-collapsible mw-collapsed" | ||
| <strong>Tipp 2 </strong> | | <strong>Tipp 2 </strong> | ||
|- | |- | ||
| Ergebnisplot:<br>[[Datei:Inf2P_5_1.jpg|left|450px|Abb. | | Legen Sie ein Bit an, welches Vorwärts- und Rückwärtsfahrt unterscheidet. | ||
|- | |||
| Setzen Sie das Bit bei Vorwärtsfahrt und löschen Sie es bei Rückwärtsfahrt. | |||
|- | |||
| Inkrementieren Sie einen <code>long</code>-Zähler im Interrupt, wenn der Motor vorwärtsfährt und dekrementieren Sie den Zähler bei Rückwärtsfahrt. | |||
|- | |||
| Rechnen Sie im <code>loop</code> bei der Ausgabe die Inkremente in eine Strecke um. | |||
|} | |||
{| role="presentation" class="wikitable mw-collapsible mw-collapsed" | |||
| <strong>Tipp 3 </strong> | |||
|- | |||
| Ergebnisplot:<br>[[Datei:Inf2P_5_1.jpg|left|450px|Abb. 2: Ergebnisdarstellung CNTL vs. CNTR]]<br> Abb. 2: CNTL/CNTR über der Zeit | |||
|} | |} | ||
---- | ---- | ||
| Zeile 51: | Zeile 71: | ||
# Kopieren Sie das Beispiel in Ihren Ordner und erweitern Sie es. | # Kopieren Sie das Beispiel in Ihren Ordner und erweitern Sie es. | ||
# Rechnen Sie die Radumdrehungen in gefahrene Strecke um. | # Rechnen Sie die Radumdrehungen in gefahrene Strecke um. | ||
# Stellen Sie die gefahrene Strecke über der Zeit in MATLAB<sup>®</sup> dar. | # Stellen Sie die gefahrene Strecke über der Zeit in MATLAB<sup>®</sup> dar (vgl. Abb. 3). | ||
'''Lernzielkontrollfragen:''' | '''Lernzielkontrollfragen:''' | ||
| Zeile 58: | Zeile 78: | ||
* Wie lässt sich die die gefahrene Strecke berechnen? | * Wie lässt sich die die gefahrene Strecke berechnen? | ||
'''Arbeitsergebnis:''' <code>testeRadInkrementalgeber.ino</code>, <code>zeigeRadInkrementalgeber.m</code> | '''Arbeitsergebnis:''' <code>testeRadInkrementalgeber.ino</code>, <code>zeigeRadInkrementalgeber.m, leseArduinoDaten.m</code> | ||
{| role="presentation" class="wikitable mw-collapsible mw-collapsed" | {| role="presentation" class="wikitable mw-collapsible mw-collapsed" | ||
| <strong>Tipp 1 </strong> | | <strong>Tipp 1 </strong> | ||
| Zeile 67: | Zeile 87: | ||
|- | |- | ||
| Aus den gemessenen Motorumdrehungen lässt sich die gefahrene Strecke berechnen: <math>U=\pi \cdot d = 3,14\cdot 6,4\,cm=20,1\,cm</math>. Drehen beider Räder um 360 °, dann fährt der Roboter 20,1 cm vorwärts. | | Aus den gemessenen Motorumdrehungen lässt sich die gefahrene Strecke berechnen: <math>U=\pi \cdot d = 3,14\cdot 6,4\,cm=20,1\,cm</math>. Drehen beider Räder um 360 °, dann fährt der Roboter 20,1 cm vorwärts. | ||
|- | |||
| Erreichen Sie die Strecke nicht, entfernen Sie als Test die Multisensorerweiterung. | |||
|} | |} | ||
{| role="presentation" class="wikitable mw-collapsible mw-collapsed" | {| role="presentation" class="wikitable mw-collapsible mw-collapsed" | ||
| <strong>Tipp 2 </strong> | | <strong>Tipp 2 </strong> | ||
|- | |- | ||
| Ergebnisplot:<br>[[Datei: | | Nutzen Sie <code>switch...case</code> um zwischen den Fahrzuständen (1: vorwärts/2: rückwärts/3: Stopp) zu wechseln. | ||
|- | |||
| Nutzen Sie die Lösung aus Aufgabe 5.2, um die Zähler zu dekrementieren und inkrementieren. | |||
|} | |||
{| role="presentation" class="wikitable mw-collapsible mw-collapsed" | |||
| <strong>Tipp 3 </strong> | |||
|- | |||
| Ergebnisplot:<br>[[Datei:Inf2P_5_2.jpg|left|450px|Abb. 3: Strecke des linken und rechten Rades]]<br> Abb. 3: Strecke des linken und rechten Rades über der Zeit | |||
|} | |} | ||
| Zeile 80: | Zeile 109: | ||
# Fahren Sie mit Ihrem Fahrzeug genau 1 m geradeaus vorwärts. | # Fahren Sie mit Ihrem Fahrzeug genau 1 m geradeaus vorwärts. | ||
# Fahren Sie wieder zum Startpunkt zurück. Wenden Sie das Fahrzeug nicht! | # Fahren Sie wieder zum Startpunkt zurück. Wenden Sie das Fahrzeug nicht! | ||
# Der AlphaBot inkrementiert die Strecke bei Vorwärtsfahrt und dekrementiert bei Rückwärtsfahrt. | # Der AlphaBot inkrementiert die Strecke bei Vorwärtsfahrt und dekrementiert bei Rückwärtsfahrt. | ||
# Stellen Sie die gefahrene Strecke im seriellen Monitor dar. | |||
'''Lernzielkontrollfragen:''' | '''Lernzielkontrollfragen:''' | ||
* Wie kann die Fahrtrichtung bei der Streckenbestimmung berücksichtigt werden? | * Wie kann die Fahrtrichtung bei der Streckenbestimmung berücksichtigt werden? | ||
* | * Wurde 1 m gefahren? Steht der AlphaBot wieder am Startpunkt? Begründen Sie ggf. die Abweichung. | ||
'''Arbeitsergebnis:''' <code>fahreVorZurueck.ino</code> | '''Arbeitsergebnis:''' <code>fahreVorZurueck.ino</code> | ||
| Zeile 94: | Zeile 124: | ||
|- | |- | ||
| Legen Sie den Akku korrekt an, um die Motoren anzusteuern. | | Legen Sie den Akku korrekt an, um die Motoren anzusteuern. | ||
|- | |||
| Wenn Ihr AlphaBot bei gleicher Ansteuerung der Motoren nicht geradeaus fährt liegt dies an den unterschiedlichen Motoren. <br> Nutzen Sie das Potentiometer der Multisensor-Erweiterung, um den „Gleichlauf der Motoren“ mit anzupassen. | |||
|- | |||
| Fazit: Eine perfekte Gerade ist nur durch Ansteuerung von Rädern nicht möglich. Die Fehler (Anfahrtmoment, unterschiedliche Motoren, Schlupf der Reifen,...) summieren sich systematisch auf. Hier hilft nur eine geregelte Geradeausfahrt (Lektion 8). | |||
|} | |} | ||
---- | ---- | ||
| Zeile 99: | Zeile 133: | ||
=== Aufgabe 5.4: Differentielle Odometrie === | === Aufgabe 5.4: Differentielle Odometrie === | ||
Odometrie bezeichnet eine Methode der Schätzung von Position und Orientierung (Lageschätzung) eines mobilen Roboters anhand der Daten seines Vortriebsystems. Durch Räder angetriebene Systeme benutzen dafür die Anzahl der Radumdrehungen, während laufende Systeme (z. B. Roboter) die Anzahl ihrer Schritte verwenden. Ein Gerät, das die Odometrie zur Lageschätzung verwendet, ist ein Odometer. Die Odometrie ist im Zusammenspiel mit der Koppelnavigation ein grundlegendes Navigationsverfahren für bodengebundene Fahrzeuge aller Art (Kraftfahrzeuge, Roboter), allerdings wird es auf Grund seiner Fehlereigenschaften selten als alleiniges Verfahren eingesetzt. In dieser Aufgabe werden die Raddrehzahlen der beiden Räder zur Lageschätzung verwendet. | Odometrie bezeichnet eine Methode der Schätzung von Position und Orientierung (Lageschätzung) eines mobilen Roboters anhand der Daten seines Vortriebsystems. Durch Räder angetriebene Systeme benutzen dafür die Anzahl der Radumdrehungen, während laufende Systeme (z. B. Roboter) die Anzahl ihrer Schritte verwenden. Ein Gerät, das die Odometrie zur Lageschätzung verwendet, ist ein Odometer. Die Odometrie ist im Zusammenspiel mit der Koppelnavigation ein grundlegendes Navigationsverfahren für bodengebundene Fahrzeuge aller Art (Kraftfahrzeuge, Roboter), allerdings wird es auf Grund seiner Fehlereigenschaften selten als alleiniges Verfahren eingesetzt. In dieser Aufgabe werden die Raddrehzahlen der beiden Räder zur Lageschätzung verwendet. | ||
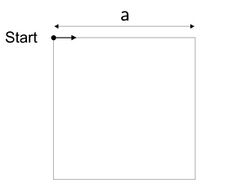
# Erweitern Sie Ihr bisheriges Programm, um die Seiten eines Quadrates im Uhrzeigersinn abzufahren (vgl. Abb. | # Erweitern Sie Ihr bisheriges Programm, um die Seiten eines Quadrates im Uhrzeigersinn abzufahren (vgl. Abb. 4). | ||
# Die Seitenlänge a ist eine Variable und soll 30 cm betragen. | # Die Seitenlänge a ist eine Variable und soll 30 cm betragen. | ||
# Führen Sie eine Schleife 4x aus, die aus Geradeausfahrt und Drehung besteht. | # Führen Sie eine Schleife 4x aus, die aus Geradeausfahrt und Drehung besteht. | ||
[[Datei:FahreQuadrat.jpg|ohne|mini|250px|Abb. 4: Fahren Sie im Uhrzeigersinn die Seiten eines Quadrates ab]] | [[Datei:FahreQuadrat.jpg|ohne|mini|250px|Abb. 4: Fahren Sie im Uhrzeigersinn die Seiten eines Quadrates ab]] | ||
'''Lernzielkontrollfragen:''' | '''Lernzielkontrollfragen:''' | ||
* | * Kommen Sie wieder am Startpunkt an? | ||
* Begründen Sie ggf. eine Abweichung. | |||
'''Arbeitsergebnis:''' <code>fahreQuadrat.ino</code> | '''Arbeitsergebnis:''' <code>fahreQuadrat.ino</code> | ||
| Zeile 118: | Zeile 152: | ||
|- | |- | ||
| Nützlicher Artikel: [https://www.mintgruen.tu-berlin.de/robotikWiki/doku.php?id=techniken:odometrie Navigation mit Differenzialantrieb] | | Nützlicher Artikel: [https://www.mintgruen.tu-berlin.de/robotikWiki/doku.php?id=techniken:odometrie Navigation mit Differenzialantrieb] | ||
|} | |||
{| role="presentation" class="wikitable mw-collapsible mw-collapsed" | |||
| <strong>Tipp 2 </strong> | |||
|- | |||
| [[Datei:Diff Odometrie.jpg|left|450px|Abb. 5: Kursbestimmung aus differentieller Odometrie]]<br> Abb. 5: Kursbestimmung aus differentieller Odometrie | |||
|- | |- | ||
|Für den Kurswinkel <math>\Psi</math> gilt: <math>\Psi=\frac{s_R-s_L}{l}</math> mit <math>l</math>: Spurweite | |Für den Kurswinkel <math>\Psi</math> gilt: <math>\Psi=\frac{s_R-s_L}{l}</math> mit <math>l</math>: Spurweite | ||
|} | |} | ||
{| role="presentation" class="wikitable mw-collapsible mw-collapsed" | {| role="presentation" class="wikitable mw-collapsible mw-collapsed" | ||
| <strong>Tipp | | <strong>Tipp 3 </strong> | ||
|- | |||
| Mitteln Sie bei Geradeausfahrt die links und rechts gefahrene Strecke. | |||
|- | |- | ||
| [ | | Drehen Sie 90° in dem Sie ein Rad vorwärts und das andere rückwärts laufen lassen. Die Kinematik der Platzdrehung ist [https://spacehal.github.io/docs/robotik/odometrie hier] beschrieben. | ||
|- | |- | ||
| | | Kapseln Sie die Platzdrehung in die Funktion <code>dreheRoboter(Winkel)</code>, wobei eine Drehung gegen den Uhrzeigersinn positiv ist. | ||
|} | |} | ||
| Zeile 149: | Zeile 190: | ||
== Literatur == | == Literatur == | ||
* [https://spacehal.github.io/docs/robotik/odometrie Lokalisierung und Odometrie eines Roboters mit differentiellem Antrieb] | |||
* [http://www.uni-ulm.de/fileadmin/website_uni_ulm/iui.inst.130/Mitarbeiter/oubbati/RobotikWS1113/Folien/Differentialantrieb.pdf Uni Ulm: Differentialantrieb.pdf] | * [http://www.uni-ulm.de/fileadmin/website_uni_ulm/iui.inst.130/Mitarbeiter/oubbati/RobotikWS1113/Folien/Differentialantrieb.pdf Uni Ulm: Differentialantrieb.pdf] | ||
* [http://www.ki.informatik.hu-berlin.de/lehre/ws0506/kogrob/KR0506Bewegung-kurz.pdf HU-Berlin Kognitive Robotik] | * [http://www.ki.informatik.hu-berlin.de/lehre/ws0506/kogrob/KR0506Bewegung-kurz.pdf HU-Berlin Kognitive Robotik] | ||
* [http://rossum.sourceforge.net/papers/DiffSteer/DiffSteer.html The Rossum Project: Differential Steering System] | * [http://rossum.sourceforge.net/papers/DiffSteer/DiffSteer.html The Rossum Project: Differential Steering System] | ||
---- | ---- | ||
→ Termine [[Einführungsveranstaltung_Informatikpraktikum_2_im_SoSe_2023|1]] [[AlphaBot:_Messdatenverarbeitung_mit_MATLAB|2]] [[AlphaBot:_MATLAB_als_serieller_Monitor|3]] [[AlphaBot: Servo ansteuern|4]] [[AlphaBot: AlphaBot: | → Termine [[Einführungsveranstaltung_Informatikpraktikum_2_im_SoSe_2023|1]] [[AlphaBot:_Messdatenverarbeitung_mit_MATLAB|2]] [[AlphaBot:_MATLAB_als_serieller_Monitor|3]] [[AlphaBot: Servo ansteuern|4]] [[AlphaBot:_Motoren_und_Inkrementalgeber|5]] [[AlphaBot: Programmier-Challenge I SoSe23|6]] [[AlphaBot:_Gesteuerte_Fahrt|7]] [[AlphaBot: Geregelte Fahrt mit Linienverfolger|8]] [[AlphaBot: Parklücke suchen|9]] [[AlphaBot: Autonomes Einparken|10]] [[AlphaBot: Programmier-Challenge II SoSe23|11]]<br> | ||
→ zurück zum Hauptartikel: [[AlphaBot_SoSe23|Informatik Praktikum 2]] | → zurück zum Hauptartikel: [[AlphaBot_SoSe23|Informatik Praktikum 2]] | ||
Aktuelle Version vom 28. April 2023, 11:13 Uhr
CNTL/CNTRAutor: Prof. Dr.-Ing. Schneider
Modul: Praxismodul I
Lehrveranstaltung: Mechatronik, Informatik Praktikum 2, 2. Semester
Inhalt
- Ansteurung der Motoren
- Auslesen der Lichtschranken via Interrupt
- Berechnung der gefahrenen Strecke
- Fahrt einer definierten Strecke und Figur.
- Berechnung des Kurswinkels aus diffenentieller Odometrie
Lernziele
Nach Durchführung dieser Lektion können Sie
- die Fahrstrecke des linken und rechten Rades aus den Lichtschrankensignale berechnen.
- eine definierte Strecke und Figur fahren.
- die Position und Lage eines mobilen Roboters mittels diffenentieller Odometrie schätzen.
Versuchsdurchführung
Aufgabe 5.1: Lichtschranke
- Bitte aktualisieren Sie ihre Arduino / librarie.
- Machen Sie sich mit dem Demo
E13_Lichtschrankevertraut, so dass Sie jede Zeile erläutern können. - Kopieren Sie das Beispiel in Ihren Ordner und erweitern Sie es.
- Lassen Sie als Test beide Motoren langsam vorwärts drehen.
- Flankenwechsel von
CNTL/CNTRsollen einen Interrupt auslösen. - Stellen Sie beide Lichtschrankenzustände
CNTL/CNTRüber der Zeit in MATLAB® dar (vgl. Abb. 2).
Lernzielkontrollfragen:
- Wie funktioniert eine Lichtschranke?
- Wo befinden sich die Lichtschranken?
- Wo ist rechts und wo links?
- An welchen Ports sind die linke und rechte Lichtschranke angeschlossen?
- Welche IO-Pins sind beim Arduino Uno interruptfähig?
- Wie entscheidet die Lichtschranke zwischen Vorwärts- oder Rückwärtsdrehung?
- Wieviele Flanken erhalten Sie für eine Radumdrehung?
Arbeitsergebnisse: testeLichtschranke.ino, testeLichtschranke.m, leseArduinoDaten.m
| Tipp 1 |
Nutzen Sie die Demos E13_Lichtschranke und E01_MotorenTest |
| Nur die IO-Pins D2 und D3 sind beim Arduino Uno interruptfähig. |
| Entfernen Sie die Multisensorerweiterung. |
| Legen Sie für eine langsame Raddrehung keine Akkus ein. Manche USB-Ports sind zu schwach um die Motoren zu betreiben. Dann müssen Sie die Akkus nutzen. |
| Tipp 2 |
| Legen Sie ein Bit an, welches Vorwärts- und Rückwärtsfahrt unterscheidet. |
| Setzen Sie das Bit bei Vorwärtsfahrt und löschen Sie es bei Rückwärtsfahrt. |
Inkrementieren Sie einen long-Zähler im Interrupt, wenn der Motor vorwärtsfährt und dekrementieren Sie den Zähler bei Rückwärtsfahrt.
|
Rechnen Sie im loop bei der Ausgabe die Inkremente in eine Strecke um.
|
| Tipp 3 |
Ergebnisplot: Abb. 2: CNTL/CNTR über der Zeit |
Aufgabe 5.2: RadInkrementalgeber
- Machen Sie sich mit
E15_RadInkrementalgeberFahrtvertraut, so dass Sie jede Zeile erläutern können. - Kopieren Sie das Beispiel in Ihren Ordner und erweitern Sie es.
- Rechnen Sie die Radumdrehungen in gefahrene Strecke um.
- Stellen Sie die gefahrene Strecke über der Zeit in MATLAB® dar (vgl. Abb. 3).
Lernzielkontrollfragen:
- Was ist ein Interrupt und wozu dient er?
- Wozu dient die Funktion
attachInterrupt()? - Wie lässt sich die die gefahrene Strecke berechnen?
Arbeitsergebnis: testeRadInkrementalgeber.ino, zeigeRadInkrementalgeber.m, leseArduinoDaten.m
| Tipp 1 |
Nutzen Sie die Demos E14_RadInkrementalgeber und E15_RadInkrementalgeberFahrt |
| Legen Sie den Akku korrekt an, um die Motoren anzusteuern. |
| Aus den gemessenen Motorumdrehungen lässt sich die gefahrene Strecke berechnen: . Drehen beider Räder um 360 °, dann fährt der Roboter 20,1 cm vorwärts. |
| Erreichen Sie die Strecke nicht, entfernen Sie als Test die Multisensorerweiterung. |
| Tipp 2 |
Nutzen Sie switch...case um zwischen den Fahrzuständen (1: vorwärts/2: rückwärts/3: Stopp) zu wechseln.
|
| Nutzen Sie die Lösung aus Aufgabe 5.2, um die Zähler zu dekrementieren und inkrementieren. |
| Tipp 3 |
Ergebnisplot: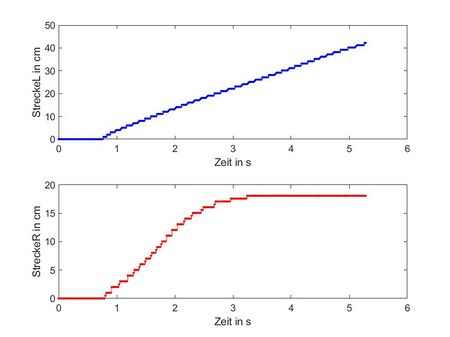 Abb. 3: Strecke des linken und rechten Rades über der Zeit |
Aufgabe 5.3: 1 m Fahrt
- Machen Sie sich mit dem Demo
E15_RadInkrementalgeberFahrtvertraut, so dass Sie jede Zeile erläutern können. - Fahren Sie mit Ihrem Fahrzeug genau 1 m geradeaus vorwärts.
- Fahren Sie wieder zum Startpunkt zurück. Wenden Sie das Fahrzeug nicht!
- Der AlphaBot inkrementiert die Strecke bei Vorwärtsfahrt und dekrementiert bei Rückwärtsfahrt.
- Stellen Sie die gefahrene Strecke im seriellen Monitor dar.
Lernzielkontrollfragen:
- Wie kann die Fahrtrichtung bei der Streckenbestimmung berücksichtigt werden?
- Wurde 1 m gefahren? Steht der AlphaBot wieder am Startpunkt? Begründen Sie ggf. die Abweichung.
Arbeitsergebnis: fahreVorZurueck.ino
| Tipp 1 |
| Nutzen Sie die Demos E01, E15, E22 im SVN-Verzeichnis. |
| Legen Sie den Akku korrekt an, um die Motoren anzusteuern. |
| Wenn Ihr AlphaBot bei gleicher Ansteuerung der Motoren nicht geradeaus fährt liegt dies an den unterschiedlichen Motoren. Nutzen Sie das Potentiometer der Multisensor-Erweiterung, um den „Gleichlauf der Motoren“ mit anzupassen. |
| Fazit: Eine perfekte Gerade ist nur durch Ansteuerung von Rädern nicht möglich. Die Fehler (Anfahrtmoment, unterschiedliche Motoren, Schlupf der Reifen,...) summieren sich systematisch auf. Hier hilft nur eine geregelte Geradeausfahrt (Lektion 8). |
Aufgabe 5.4: Differentielle Odometrie
Odometrie bezeichnet eine Methode der Schätzung von Position und Orientierung (Lageschätzung) eines mobilen Roboters anhand der Daten seines Vortriebsystems. Durch Räder angetriebene Systeme benutzen dafür die Anzahl der Radumdrehungen, während laufende Systeme (z. B. Roboter) die Anzahl ihrer Schritte verwenden. Ein Gerät, das die Odometrie zur Lageschätzung verwendet, ist ein Odometer. Die Odometrie ist im Zusammenspiel mit der Koppelnavigation ein grundlegendes Navigationsverfahren für bodengebundene Fahrzeuge aller Art (Kraftfahrzeuge, Roboter), allerdings wird es auf Grund seiner Fehlereigenschaften selten als alleiniges Verfahren eingesetzt. In dieser Aufgabe werden die Raddrehzahlen der beiden Räder zur Lageschätzung verwendet.
- Erweitern Sie Ihr bisheriges Programm, um die Seiten eines Quadrates im Uhrzeigersinn abzufahren (vgl. Abb. 4).
- Die Seitenlänge a ist eine Variable und soll 30 cm betragen.
- Führen Sie eine Schleife 4x aus, die aus Geradeausfahrt und Drehung besteht.
Lernzielkontrollfragen:
- Kommen Sie wieder am Startpunkt an?
- Begründen Sie ggf. eine Abweichung.
Arbeitsergebnis: fahreQuadrat.ino
| Tipp 1 |
| Nutzen Sie die Demos E01, E15, E22 im SVN-Verzeichnis. |
| Legen Sie den Akku korrekt an, um die Motoren anzusteuern. |
| Nützlicher Artikel: Navigation mit Differenzialantrieb |
| Tipp 2 |
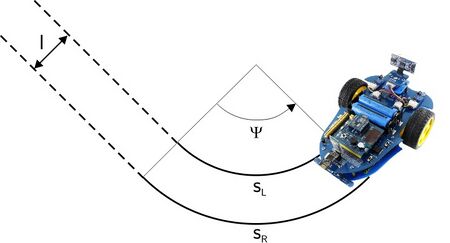 Abb. 5: Kursbestimmung aus differentieller Odometrie |
| Für den Kurswinkel gilt: mit : Spurweite |
| Tipp 3 |
| Mitteln Sie bei Geradeausfahrt die links und rechts gefahrene Strecke. |
| Drehen Sie 90° in dem Sie ein Rad vorwärts und das andere rückwärts laufen lassen. Die Kinematik der Platzdrehung ist hier beschrieben. |
Kapseln Sie die Platzdrehung in die Funktion dreheRoboter(Winkel), wobei eine Drehung gegen den Uhrzeigersinn positiv ist.
|
Aufgabe 5.5: Nachhaltige Doku
Sichern Sie alle Ergebnisse mit beschreibendem Text (message) in SVN.
- Halten Sie die Regeln für den Umgang mit SVN ein.
- Halten Sie die Programmierrichtlinie für C und die Programmierrichtlinien für MATLAB® ein.
- Versehen Sie jedes Programm mit einem Header (Header Beispiel für MATLAB, Header Beispiel für C).
- Kommentiere Sie den Quelltext umfangreich.
Arbeitsergebnis in SVN: SVN Log
Tutorials
Demos
Literatur
- Lokalisierung und Odometrie eines Roboters mit differentiellem Antrieb
- Uni Ulm: Differentialantrieb.pdf
- HU-Berlin Kognitive Robotik
- The Rossum Project: Differential Steering System
→ Termine 1 2 3 4 5 6 7 8 9 10 11
→ zurück zum Hauptartikel: Informatik Praktikum 2