Automatische Kamera Kalibrierung: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
|||
| (15 dazwischenliegende Versionen von einem anderen Benutzer werden nicht angezeigt) | |||
| Zeile 13: | Zeile 13: | ||
# Transformieren Sie das Referenzmuster aus der Kameraperspektive in Weltkoordinaten. | # Transformieren Sie das Referenzmuster aus der Kameraperspektive in Weltkoordinaten. | ||
# Stellen Sie die Objekte im Sichtfeld in 3D metrisch dar. | # Stellen Sie die Objekte im Sichtfeld in 3D metrisch dar. | ||
# Schätzen Sie die Genauigkeit Ihres | # Schätzen Sie die Genauigkeit Ihres Algorithmus ab. | ||
# Zeigen Sie, dass Objekte | # Zeigen Sie, dass Objekte bekannter Größe mit Ihrer Kalibrierung metrisch vermessen werden können. | ||
# Wissenschaftliche Dokumentation als HSHL-Wiki Artikel | # Wissenschaftliche Dokumentation als HSHL-Wiki Artikel | ||
# Softwareentwicklung nach SDE Standard in SVN | # Softwareentwicklung nach SDE Standard in SVN | ||
| Zeile 21: | Zeile 21: | ||
== Lösungen == | == Lösungen == | ||
===Automatische Kamerakalibrierung anhand eines Referenzmusters=== | |||
Zu Beginn des Matlab-Skripts wird eine Initialisierung vorgenommen, sodass alle Variablen im Workspace gelöscht, offene Fenster geschlossen und das Command Window geleert wird. | |||
<source lang="matlab"> | |||
%% Initialisierung | |||
clear all; | |||
close all; | |||
clc; | |||
</source> | |||
Der nachfolgende Bereich enthält Variablen, die die zur automatischen Kalibrierung verwendeten Daten enthalten. Dazu gehört die Anzahl der aufzunehmenden Bilder, die Zeit zwischen der Aufnahme dieser Bilder und die Größe der Schachbrettquadrate des verwendeten Referenzmusters. | |||
<source lang="matlab"> | |||
%% Eingabe der Daten zur automatischen Kamerakalibrierung | |||
amountOfImages = 5; % Anzahl der zur Kalibrierung aufzunehmenden Bilder | |||
delaytime = 5; % Verzögerung zwischen der Aufnahme der Kalibrierungsfotos | |||
squareSize = 21; % Größe der Schachbrettquadrate in mm | |||
</source> | |||
Im nächsten Schritt werden die Kalibrierungsbilder mittels Webcam erstellt. Dazu wird die Webcam aktiviert und in einen vorher erstellten Ordner gewechselt, in dem die Kalibrierungsbilder gespeichert werden sollen. In einer For-Schleife über die Anzahl der Bilder werden diese aufgenommen, auf dem Bildschirm ausgegeben und in dem zuvor erwähnten Ordner als .png Datei gespeichert. | |||
<source lang="matlab"> | |||
%% Aufnehmen der Kalibrierungsbilder mittels Webcam | |||
cam = webcam; % Starten der Webcam | |||
cd('Kalibrierung') % Ordner zur Speicherung der Kalibrierungsbilder | |||
for i= 1:amountOfImages | |||
img = snapshot(cam); % Aufnahme des Webcam-Bildes | |||
imagesc(img); % Ausgabe des Bildes | |||
axis image; % Achsen an Größe des Bildes anpassen | |||
axis off; % Skalierung der Achsen nicht anzeigen | |||
char = int2str(i); % Umwandeln des Bildindex in Text | |||
filename = (['image' char '.png']); % Zusammensetzen des Speichernamen des Bildes | |||
imwrite (img,filename) % Speichern des Bildes | |||
pause (delaytime); % Zeit bis zur Aufnahme des nächsten Webcam-Bildes | |||
end | |||
</source> | |||
Es folgt die Kalibrierung der zur Aufnahme verwendeten Webcam durch Erkennung des Referenzmusters auf den Kalibrierungsbildern. Dazu werden die Kalibrierungsbilder zuerst als Datastore eingelesen, sodass sie nachfolgenden Funktionen als eine Einheit übergeben werden können. Die nachfolgende Funktion "detectCheckerboardPoints" der Camera Calibration Toolbox von Matlab erkennt für jedes im Datastore eingelesene Bild die Ecken auf dem Referenzmuster sowie die Größe dieses Referenzmusters in Schachbrettquadraten. In der darauffolgenden Funktion "generateCheckerboardPoints" werden über die ermittelte Größe des Referenzmusters und die Größe der darauf enthaltenen Schachbrettquadrate die Weltkoordinaten der Ecken dieser Quadrate ermittelt. Zuletzt wird die Webcam mit der Funktion "estimateCameraParameters" über die Größe der Kalibrierungsbilder und die Lage der darauf befindlichen Schachbrettecken, sowohl in Pixel- als auch in Weltkoordinaten, kalibriert. Dabei werden die intrinsischen und extrinsischen Kameraparameter, die Linsenverzerrungskoeffizienten sowie die Genauigkeit des Kalibrierungsalgorithmus bestimmt. | |||
<source lang="matlab"> | |||
%% Kalibrieren der Webcam durch Erkennung des Schachbrettmusters in den Kalibrierungsbildern | |||
images = imageDatastore(fullfile('/Users/madlen/Desktop/DSB/User/SoSe2018/Madlen Bartnick/Kalibrierung')); % Einrichten eines Datastores für die Kalibrierungsbilder | |||
imageFileNames = images.Files; % Einlesen der gespeicheten Kalibrierungsbilder | |||
[imagePoints, boardSize ] = detectCheckerboardPoints(imageFileNames); % MATLAB Funktion zur automatischen Erkennung der Schachbrettecken in Pixelkoordinaten | |||
worldPoints = generateCheckerboardPoints(boardSize,squareSize); % MATLAB Funktion zur Transformation der Schachbrettecken in Weltkoordinaten | |||
imageSize = [size(images, 1), size(images, 2)]; % Berechnung der Bildgröße | |||
cameraParams = estimateCameraParameters(imagePoints, worldPoints, ... % MATLAB Funktion zur Errechnung der Kameraparameter | |||
'ImageSize', imageSize); | |||
</source> | |||
[[Datei:Ergebnisse der Kalibration.png|mini|232px|Abb. 1 Bildschirmausgabe der Kalibrationsergebnisse]] | |||
Im nachfolgenden Programmabschnitt wird die Ausgabe der Kalibrationsergebnisse in einem gemeinsamen Fenster realisiert. Dazu werden zum einen ein zur Kalibrierung aufgenommenes Bild, zum anderen dieses Bild mit den vom Kalibrierungsalgorithmus erkannten und reproduzierten Schachbrettecken ausgegeben. Eine weitere Grafik zeigt die extrinsischen Kameraparameter als 3D metrische Darstellung der Lage von Kamera und Kalibrierungsbilder zueinander. Ebenfalls wird ein Balkendiagramm ausgegeben, welches die Genauigkeit des Kalibrierungsalgorithmus für jedes Bild sowie den Durchschnitt aller verwendeten Bilder visualisiert. | |||
Abb. 1 Zeigt die auf dem Bildschirm ausgegebenen Kalibrationsergebnisse. | |||
<source lang="matlab"> | |||
%% Ausgabe der Kalibrationsergebnisse | |||
figure('units','normalized','outerposition',[0 0 1 1]); % Ausgabe auf dem gesamten Bildschirm | |||
% Ausgabe eines zur Kalibrierung verwendeten Bildes | |||
ax(1)= subplot(2,2,1); | |||
imshow(imageFileNames{1}); | |||
title('Erstes Kalibrationsbild'); | |||
% Ausgabe eines Kalibrierungsbildes mit erkannten und reproduzierten Schachbildecken | |||
ax(2)= subplot(2,2,2); | |||
imshow(imageFileNames{1}); | |||
hold on | |||
plot(imagePoints(:, 1, 1), imagePoints(:, 2, 1), 'go'); | |||
plot(cameraParams.ReprojectedPoints(:, 1, 1), cameraParams.ReprojectedPoints(:, 2, 1), 'r+'); | |||
legend('Detected Points', 'ReprojectedPoints'); | |||
hold off | |||
title('Erkanntes Schachbrett') | |||
imagePoints = zeros; % Zurücksetzen der Bildpunktmatrix | |||
% Ausgabe der extrinsischen Kameraparameter | |||
ax(3)= subplot(2,2,3); | |||
showExtrinsics(cameraParams); | |||
title('Extrinsische Kameraparameter') | |||
drawnow; | |||
% Ausgabe der errechneten Genauigkeit in Pixel | |||
ax(4)= subplot(2,2,4); | |||
showReprojectionErrors(cameraParams); | |||
title('Fehler bei Schachbrettreproduktion'); | |||
</source> | |||
===Metrische Vermessung einer Münze neben dem Referenzmuster=== | |||
Zur metrischen Vermessung einer Münze wird das erste Kalibrierungsbild aus dem Datastore eingelesen. Es folgen mehrere Schritte der Bildverarbeitung, um die Münze im Bild zu segmentieren. Zuerst wird durch die Funktion "undistortImage" über die durch die Kalibrierung ermittelten Kameraparameter die Linsenverzerrung des Bildes korrigiert. Im nächsten Schritt wird das Bild vom RGB- in den HSV-Farbraum gewandelt, um es anschließend in ein Farbsättigungsbild umzuwandeln. Über die Farbsättigung lässt sich die Münze sehr gut vom schwarz-weißen Referenzmuster unterscheiden. Über die Funktion "graythresh" wird der optimale Schwellwert für Grauwerte in dem vorliegenden Farbsättigungsbild ermittelt. Mit Hilfe dieses Schwellwerts wird das Farbsättigungsbild in ein Binärbild gewandelt und damit die Segmentierung abgeschlossen. | |||
<source lang="matlab"> | |||
%% Bearbeitung des Bildes zur Segmentierung einer Münze | |||
image=imread(imageFileNames{1}); % Einlesen des ersten Kalibrierungbildes | |||
correctedImage = undistortImage(image, cameraParams ); % MATLAB Funktion zur Beseitigung der Linsenverzerrung | |||
HSVImage= rgb2hsv(correctedImage); % Umwandlung des Bildes vom RGB Farbraum in den HSV Farbraum | |||
saturationImage = HSVImage (:, :, 2); % Umwandlung in ein Farbsättigungsbild | |||
threshold = graythresh(saturationImage); % Automatische Bestimmung eines Schwellwerts für Grauwerte | |||
binaryImage = (saturationImage > threshold); % Umwandlung in ein Binärbild mittels Schwellwertoperation | |||
</source> | |||
Nach der Segmentierung der Münze im Bild muss diese im nächsten Programmabschnitt erkannt werden. Dazu wird zuerst eine Blob-Analyse durchgeführt, die zusammenhängende Segmente im Binärbild erkennt und die dazugehörigen Flächeninhalte und Positionen ausgibt. Die Blob-Analyse ist hier so konfiguriert, dass die Position der Segmente durch die Ecken eines an allen Seiten anliegenden Rechtecks beschrieben werden. Zudem ist eine Mindestgröße für die zu erkennenden Segmente von 200 Pixeln festgelegt. Des Weiteren werden Pixel, die die Grenze des Segments bilden nicht zu dem Segment gezählt. Nach der Blob-Analyse werden die dadurch ermittelten Segmentflächen mit zugehörigen Positionen über den "sort" Befehl nach der Größe absteigend sortiert. Bei dem größten erkannten Segment handelt es sich um die im Bild erkannte Münze. Über die Funktion "insertObjectAnnotation" wird in dem Bild an der Position des größten Segments ein rechteckiges Label mit der Aufschrift "Münze" eingefügt und die Erkennung abgeschlossen. | |||
<source lang="matlab"> | |||
%% Erkennung der Münze im Bild | |||
blobAnalysis = vision.BlobAnalysis('AreaOutputPort', true,... % MATLAB Funktion zur Erkennung von Segmenten | |||
'CentroidOutputPort', false,... | |||
'BoundingBoxOutputPort', true,... | |||
'MinimumBlobArea', 200, 'ExcludeBorderBlobs', true); | |||
[areas, positions] = step(blobAnalysis, binaryImage); % Fläche und Position der Segmente | |||
[~, index] = sort(areas, 'Descend'); % Sortierung nach Größe der Fläche | |||
positionOfCoin=positions(index(1:1),:); % Position des größten Elements ist Position der Münze | |||
areaOfCoin= areas(index(1:1),:); % Fläche des größten Elements ist Fläche der Münze | |||
coinImage = insertObjectAnnotation(correctedImage, 'rectangle', ... % Hinzufügen eines Labels für die erkannte Münze | |||
positionOfCoin, 'Münze'); | |||
</source> | |||
[[Datei:Ergebnisse der Erkennung.png|mini|232px|Abb. 2 Bildschirmausgabe der Erkennung einer Münze im Bild]] | |||
Durch den nachfolgenden Programmabschnitt werden die Ergebnisse der Segmentierung und Detektion der Münze in einem gemeinsamen Fenster ausgegeben. Dazu wird das Originalbild vor und nach der Korrektur der Linsenverzerrung ausgegeben. Ebenso wird die Segmentierung der Münze im Binärbild und die dadurch erkannte Münze im verzerrungsfreien Originalbild angezeigt. | |||
Abb. 2 Zeigt die auf dem Bildschirm ausgegebenen Ergebnisse der Segmentierung und Detektion. | |||
<source lang="matlab"> | |||
%% Ausgabe der Ergebnisse der Segmentierung und Detektion der Münze | |||
% Ausgabe des Originalbildes bevor der Verarbeitung | |||
figure('units','normalized','outerposition',[0 0 1 1]); % Ausgabe auf dem gesamten Bildschirm | |||
ax(1)= subplot(2,2,1); | |||
imshow(imageFileNames{1}); | |||
title('Original Bild') | |||
% Ausgabe des Bildes nachdem die Linsenverzerrung korrigiert wurde | |||
ax(2)= subplot(2,2,2); | |||
imshow(correctedImage); | |||
title('Verzerrungsfreies Bild') | |||
% Ausgabe des zur Erkennung verwendeten Binärbildes | |||
ax(3)= subplot(2,2,3); | |||
imshow(binaryImage); | |||
hold on; | |||
title('Binärbild') | |||
% Ausgabe des Bildes mit Label für die erkannte Münze | |||
ax(4)= subplot(2,2,4); | |||
imshow(coinImage); | |||
title('Erkannte Münze') | |||
</source> | |||
Zur Vermessung der Münze werden im ersten Schritt die oberen Ecken des Münzlabels zu einem Punktepaar zusammengefasst. im nächsten Schritt werden über die Funktionen "detectCherckerboardPoints" und "extrinsics" die extrinsischen Kameraparameter bei der Aufnahme des verwendeten Bildes ermittelt, um die oberen Labelecken in Pixelkoordinaten mit der Funktion "pointsToWorld" in Weltkoordinaten umzurechnen. Zuletzt wird über die Differenz der Labelecken in Weltkoordinaten die Euklidische Distanz dieser Ecken zueinander berechnet, welche dem Durchmesser der Münze in mm entspricht. | |||
<source lang="matlab"> | |||
%% Vermessung der Münze | |||
upperLeftCornerX = positionOfCoin(1); | |||
upperLeftCornerY = positionOfCoin(2); | |||
upperLeftCorner = [upperLeftCornerX,upperLeftCornerY]; % Labelecke oben links in Pixel | |||
upperRightCornerX = positionOfCoin(1)+positionOfCoin(3); | |||
upperRightCornerY = positionOfCoin (2); | |||
upperRightCorner = [upperRightCornerX, upperRightCornerY]; % Labelecke oben rechts in Pixel | |||
upperCornersInPixel = [upperLeftCorner;upperRightCorner]; % Obere Labelecken in Pixel | |||
[imagePoints, boardSize] = detectCheckerboardPoints(image); % Erkennung der Schachbrettquadrate | |||
[R, t] = extrinsics(imagePoints, worldPoints, cameraParams); % Ermittlung der extrinsischen Kameraparameter bei Aufnahme des Bildes | |||
upperCornersInWorld = pointsToWorld(cameraParams, R, t, upperCornersInPixel); % Transformieren der Labelecken in Weltkoordinaten | |||
diffWorld = upperCornersInWorld(2, :) - upperCornersInWorld(1, :); % Differenz zwischen oberen Labelecken in Weltkoordinaten | |||
diameterInMillimeter = hypot(diffWorld(1), diffWorld(2)); % Euklidische Distanz zwischen oberen Labelecken entspricht dem Durchmesser der Münze in Weltkoordinaten (mm) | |||
</source> | |||
[[Datei:Ergebnisse der Vermessung.png|mini|232px|Abb. 3 Ergebnis der Vermessung]] | |||
Durch den nachfolgenden Programmteil werden mit dem "fprintf" Befehl das zu erwartende sowie das tatsächliche Ergebnis der Vermessung der Münze im Command Window ausgegeben. | |||
Abb. 3 Zeigt das im Command Window ausgegebene Ergebnis | |||
<source lang="matlab"> | |||
%% Ausgabe der Vermessungsergebnisse | |||
fprintf('Tatsächlicher Durchmesser der Münze: 29 mm\n'); % Ausgabe des tatsächlichen Durchmessers im Command Window | |||
fprintf('Gemessener Durchmesser der Münze: %0.2f mm\n', diameterInMillimeter); % Ausgabe des gemessenen Durchmessers im Command Window | |||
</source> | |||
Zum Beenden des Programms wird in das ursprüngliche Verzeichnis zurückgewechselt und die Webcam gestoppt. | |||
<source lang="matlab"> | |||
%% Beenden | |||
cd('/Users/madlen/Desktop/DSB/User/SoSe2018/Madlen Bartnick') | |||
delete(cam); | |||
</source> | |||
=== Videobeweis === | |||
Als Nachweis und zur Veranschaulichung der Funktion dieses Programms dient dieses [https://youtu.be/TSjfieXnUO4 Youtube Video]. | |||
== Weblinks == | == Weblinks == | ||
Aktuelle Version vom 5. September 2018, 13:29 Uhr
Autor: Madlen Bartnick
Betreuer: Prof. Schneider
Motivation
Kameras haben intrinsische und extrinsische Parameter, welche kalibriert werden müssen.
Ziel
Matlab hat bereits eine Kalibriertoolbox. Diese soll nun so automatisiert werden, dass bei fester Kameraposition die intrinsischen und extrinsischen Parameter automatisch kalibriert werden.
Anforderungen
- Machen Sie sich mit der Kalibriertoolbox von Matlab bekannt.
- Anhand eines Referenzmusters, welches vor der Kamera an verschiedene Positionen bewegt wird, sollen die Kameraparameter bestimmt werden.
- Transformieren Sie das Referenzmuster aus der Kameraperspektive in Weltkoordinaten.
- Stellen Sie die Objekte im Sichtfeld in 3D metrisch dar.
- Schätzen Sie die Genauigkeit Ihres Algorithmus ab.
- Zeigen Sie, dass Objekte bekannter Größe mit Ihrer Kalibrierung metrisch vermessen werden können.
- Wissenschaftliche Dokumentation als HSHL-Wiki Artikel
- Softwareentwicklung nach SDE Standard in SVN
- Funktionsnachweis als YouTube-Video (vgl. Veranstaltungsregeln)
Lösungen
Automatische Kamerakalibrierung anhand eines Referenzmusters
Zu Beginn des Matlab-Skripts wird eine Initialisierung vorgenommen, sodass alle Variablen im Workspace gelöscht, offene Fenster geschlossen und das Command Window geleert wird.
%% Initialisierung
clear all;
close all;
clc;
Der nachfolgende Bereich enthält Variablen, die die zur automatischen Kalibrierung verwendeten Daten enthalten. Dazu gehört die Anzahl der aufzunehmenden Bilder, die Zeit zwischen der Aufnahme dieser Bilder und die Größe der Schachbrettquadrate des verwendeten Referenzmusters.
%% Eingabe der Daten zur automatischen Kamerakalibrierung
amountOfImages = 5; % Anzahl der zur Kalibrierung aufzunehmenden Bilder
delaytime = 5; % Verzögerung zwischen der Aufnahme der Kalibrierungsfotos
squareSize = 21; % Größe der Schachbrettquadrate in mm
Im nächsten Schritt werden die Kalibrierungsbilder mittels Webcam erstellt. Dazu wird die Webcam aktiviert und in einen vorher erstellten Ordner gewechselt, in dem die Kalibrierungsbilder gespeichert werden sollen. In einer For-Schleife über die Anzahl der Bilder werden diese aufgenommen, auf dem Bildschirm ausgegeben und in dem zuvor erwähnten Ordner als .png Datei gespeichert.
%% Aufnehmen der Kalibrierungsbilder mittels Webcam
cam = webcam; % Starten der Webcam
cd('Kalibrierung') % Ordner zur Speicherung der Kalibrierungsbilder
for i= 1:amountOfImages
img = snapshot(cam); % Aufnahme des Webcam-Bildes
imagesc(img); % Ausgabe des Bildes
axis image; % Achsen an Größe des Bildes anpassen
axis off; % Skalierung der Achsen nicht anzeigen
char = int2str(i); % Umwandeln des Bildindex in Text
filename = (['image' char '.png']); % Zusammensetzen des Speichernamen des Bildes
imwrite (img,filename) % Speichern des Bildes
pause (delaytime); % Zeit bis zur Aufnahme des nächsten Webcam-Bildes
end
Es folgt die Kalibrierung der zur Aufnahme verwendeten Webcam durch Erkennung des Referenzmusters auf den Kalibrierungsbildern. Dazu werden die Kalibrierungsbilder zuerst als Datastore eingelesen, sodass sie nachfolgenden Funktionen als eine Einheit übergeben werden können. Die nachfolgende Funktion "detectCheckerboardPoints" der Camera Calibration Toolbox von Matlab erkennt für jedes im Datastore eingelesene Bild die Ecken auf dem Referenzmuster sowie die Größe dieses Referenzmusters in Schachbrettquadraten. In der darauffolgenden Funktion "generateCheckerboardPoints" werden über die ermittelte Größe des Referenzmusters und die Größe der darauf enthaltenen Schachbrettquadrate die Weltkoordinaten der Ecken dieser Quadrate ermittelt. Zuletzt wird die Webcam mit der Funktion "estimateCameraParameters" über die Größe der Kalibrierungsbilder und die Lage der darauf befindlichen Schachbrettecken, sowohl in Pixel- als auch in Weltkoordinaten, kalibriert. Dabei werden die intrinsischen und extrinsischen Kameraparameter, die Linsenverzerrungskoeffizienten sowie die Genauigkeit des Kalibrierungsalgorithmus bestimmt.
%% Kalibrieren der Webcam durch Erkennung des Schachbrettmusters in den Kalibrierungsbildern
images = imageDatastore(fullfile('/Users/madlen/Desktop/DSB/User/SoSe2018/Madlen Bartnick/Kalibrierung')); % Einrichten eines Datastores für die Kalibrierungsbilder
imageFileNames = images.Files; % Einlesen der gespeicheten Kalibrierungsbilder
[imagePoints, boardSize ] = detectCheckerboardPoints(imageFileNames); % MATLAB Funktion zur automatischen Erkennung der Schachbrettecken in Pixelkoordinaten
worldPoints = generateCheckerboardPoints(boardSize,squareSize); % MATLAB Funktion zur Transformation der Schachbrettecken in Weltkoordinaten
imageSize = [size(images, 1), size(images, 2)]; % Berechnung der Bildgröße
cameraParams = estimateCameraParameters(imagePoints, worldPoints, ... % MATLAB Funktion zur Errechnung der Kameraparameter
'ImageSize', imageSize);
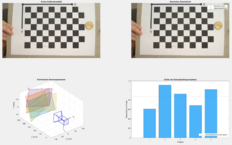
Im nachfolgenden Programmabschnitt wird die Ausgabe der Kalibrationsergebnisse in einem gemeinsamen Fenster realisiert. Dazu werden zum einen ein zur Kalibrierung aufgenommenes Bild, zum anderen dieses Bild mit den vom Kalibrierungsalgorithmus erkannten und reproduzierten Schachbrettecken ausgegeben. Eine weitere Grafik zeigt die extrinsischen Kameraparameter als 3D metrische Darstellung der Lage von Kamera und Kalibrierungsbilder zueinander. Ebenfalls wird ein Balkendiagramm ausgegeben, welches die Genauigkeit des Kalibrierungsalgorithmus für jedes Bild sowie den Durchschnitt aller verwendeten Bilder visualisiert.
Abb. 1 Zeigt die auf dem Bildschirm ausgegebenen Kalibrationsergebnisse.
%% Ausgabe der Kalibrationsergebnisse
figure('units','normalized','outerposition',[0 0 1 1]); % Ausgabe auf dem gesamten Bildschirm
% Ausgabe eines zur Kalibrierung verwendeten Bildes
ax(1)= subplot(2,2,1);
imshow(imageFileNames{1});
title('Erstes Kalibrationsbild');
% Ausgabe eines Kalibrierungsbildes mit erkannten und reproduzierten Schachbildecken
ax(2)= subplot(2,2,2);
imshow(imageFileNames{1});
hold on
plot(imagePoints(:, 1, 1), imagePoints(:, 2, 1), 'go');
plot(cameraParams.ReprojectedPoints(:, 1, 1), cameraParams.ReprojectedPoints(:, 2, 1), 'r+');
legend('Detected Points', 'ReprojectedPoints');
hold off
title('Erkanntes Schachbrett')
imagePoints = zeros; % Zurücksetzen der Bildpunktmatrix
% Ausgabe der extrinsischen Kameraparameter
ax(3)= subplot(2,2,3);
showExtrinsics(cameraParams);
title('Extrinsische Kameraparameter')
drawnow;
% Ausgabe der errechneten Genauigkeit in Pixel
ax(4)= subplot(2,2,4);
showReprojectionErrors(cameraParams);
title('Fehler bei Schachbrettreproduktion');
Metrische Vermessung einer Münze neben dem Referenzmuster
Zur metrischen Vermessung einer Münze wird das erste Kalibrierungsbild aus dem Datastore eingelesen. Es folgen mehrere Schritte der Bildverarbeitung, um die Münze im Bild zu segmentieren. Zuerst wird durch die Funktion "undistortImage" über die durch die Kalibrierung ermittelten Kameraparameter die Linsenverzerrung des Bildes korrigiert. Im nächsten Schritt wird das Bild vom RGB- in den HSV-Farbraum gewandelt, um es anschließend in ein Farbsättigungsbild umzuwandeln. Über die Farbsättigung lässt sich die Münze sehr gut vom schwarz-weißen Referenzmuster unterscheiden. Über die Funktion "graythresh" wird der optimale Schwellwert für Grauwerte in dem vorliegenden Farbsättigungsbild ermittelt. Mit Hilfe dieses Schwellwerts wird das Farbsättigungsbild in ein Binärbild gewandelt und damit die Segmentierung abgeschlossen.
%% Bearbeitung des Bildes zur Segmentierung einer Münze
image=imread(imageFileNames{1}); % Einlesen des ersten Kalibrierungbildes
correctedImage = undistortImage(image, cameraParams ); % MATLAB Funktion zur Beseitigung der Linsenverzerrung
HSVImage= rgb2hsv(correctedImage); % Umwandlung des Bildes vom RGB Farbraum in den HSV Farbraum
saturationImage = HSVImage (:, :, 2); % Umwandlung in ein Farbsättigungsbild
threshold = graythresh(saturationImage); % Automatische Bestimmung eines Schwellwerts für Grauwerte
binaryImage = (saturationImage > threshold); % Umwandlung in ein Binärbild mittels Schwellwertoperation
Nach der Segmentierung der Münze im Bild muss diese im nächsten Programmabschnitt erkannt werden. Dazu wird zuerst eine Blob-Analyse durchgeführt, die zusammenhängende Segmente im Binärbild erkennt und die dazugehörigen Flächeninhalte und Positionen ausgibt. Die Blob-Analyse ist hier so konfiguriert, dass die Position der Segmente durch die Ecken eines an allen Seiten anliegenden Rechtecks beschrieben werden. Zudem ist eine Mindestgröße für die zu erkennenden Segmente von 200 Pixeln festgelegt. Des Weiteren werden Pixel, die die Grenze des Segments bilden nicht zu dem Segment gezählt. Nach der Blob-Analyse werden die dadurch ermittelten Segmentflächen mit zugehörigen Positionen über den "sort" Befehl nach der Größe absteigend sortiert. Bei dem größten erkannten Segment handelt es sich um die im Bild erkannte Münze. Über die Funktion "insertObjectAnnotation" wird in dem Bild an der Position des größten Segments ein rechteckiges Label mit der Aufschrift "Münze" eingefügt und die Erkennung abgeschlossen.
%% Erkennung der Münze im Bild
blobAnalysis = vision.BlobAnalysis('AreaOutputPort', true,... % MATLAB Funktion zur Erkennung von Segmenten
'CentroidOutputPort', false,...
'BoundingBoxOutputPort', true,...
'MinimumBlobArea', 200, 'ExcludeBorderBlobs', true);
[areas, positions] = step(blobAnalysis, binaryImage); % Fläche und Position der Segmente
[~, index] = sort(areas, 'Descend'); % Sortierung nach Größe der Fläche
positionOfCoin=positions(index(1:1),:); % Position des größten Elements ist Position der Münze
areaOfCoin= areas(index(1:1),:); % Fläche des größten Elements ist Fläche der Münze
coinImage = insertObjectAnnotation(correctedImage, 'rectangle', ... % Hinzufügen eines Labels für die erkannte Münze
positionOfCoin, 'Münze');

Durch den nachfolgenden Programmabschnitt werden die Ergebnisse der Segmentierung und Detektion der Münze in einem gemeinsamen Fenster ausgegeben. Dazu wird das Originalbild vor und nach der Korrektur der Linsenverzerrung ausgegeben. Ebenso wird die Segmentierung der Münze im Binärbild und die dadurch erkannte Münze im verzerrungsfreien Originalbild angezeigt.
Abb. 2 Zeigt die auf dem Bildschirm ausgegebenen Ergebnisse der Segmentierung und Detektion.
%% Ausgabe der Ergebnisse der Segmentierung und Detektion der Münze
% Ausgabe des Originalbildes bevor der Verarbeitung
figure('units','normalized','outerposition',[0 0 1 1]); % Ausgabe auf dem gesamten Bildschirm
ax(1)= subplot(2,2,1);
imshow(imageFileNames{1});
title('Original Bild')
% Ausgabe des Bildes nachdem die Linsenverzerrung korrigiert wurde
ax(2)= subplot(2,2,2);
imshow(correctedImage);
title('Verzerrungsfreies Bild')
% Ausgabe des zur Erkennung verwendeten Binärbildes
ax(3)= subplot(2,2,3);
imshow(binaryImage);
hold on;
title('Binärbild')
% Ausgabe des Bildes mit Label für die erkannte Münze
ax(4)= subplot(2,2,4);
imshow(coinImage);
title('Erkannte Münze')
Zur Vermessung der Münze werden im ersten Schritt die oberen Ecken des Münzlabels zu einem Punktepaar zusammengefasst. im nächsten Schritt werden über die Funktionen "detectCherckerboardPoints" und "extrinsics" die extrinsischen Kameraparameter bei der Aufnahme des verwendeten Bildes ermittelt, um die oberen Labelecken in Pixelkoordinaten mit der Funktion "pointsToWorld" in Weltkoordinaten umzurechnen. Zuletzt wird über die Differenz der Labelecken in Weltkoordinaten die Euklidische Distanz dieser Ecken zueinander berechnet, welche dem Durchmesser der Münze in mm entspricht.
%% Vermessung der Münze
upperLeftCornerX = positionOfCoin(1);
upperLeftCornerY = positionOfCoin(2);
upperLeftCorner = [upperLeftCornerX,upperLeftCornerY]; % Labelecke oben links in Pixel
upperRightCornerX = positionOfCoin(1)+positionOfCoin(3);
upperRightCornerY = positionOfCoin (2);
upperRightCorner = [upperRightCornerX, upperRightCornerY]; % Labelecke oben rechts in Pixel
upperCornersInPixel = [upperLeftCorner;upperRightCorner]; % Obere Labelecken in Pixel
[imagePoints, boardSize] = detectCheckerboardPoints(image); % Erkennung der Schachbrettquadrate
[R, t] = extrinsics(imagePoints, worldPoints, cameraParams); % Ermittlung der extrinsischen Kameraparameter bei Aufnahme des Bildes
upperCornersInWorld = pointsToWorld(cameraParams, R, t, upperCornersInPixel); % Transformieren der Labelecken in Weltkoordinaten
diffWorld = upperCornersInWorld(2, :) - upperCornersInWorld(1, :); % Differenz zwischen oberen Labelecken in Weltkoordinaten
diameterInMillimeter = hypot(diffWorld(1), diffWorld(2)); % Euklidische Distanz zwischen oberen Labelecken entspricht dem Durchmesser der Münze in Weltkoordinaten (mm)

Durch den nachfolgenden Programmteil werden mit dem "fprintf" Befehl das zu erwartende sowie das tatsächliche Ergebnis der Vermessung der Münze im Command Window ausgegeben.
Abb. 3 Zeigt das im Command Window ausgegebene Ergebnis
%% Ausgabe der Vermessungsergebnisse
fprintf('Tatsächlicher Durchmesser der Münze: 29 mm\n'); % Ausgabe des tatsächlichen Durchmessers im Command Window
fprintf('Gemessener Durchmesser der Münze: %0.2f mm\n', diameterInMillimeter); % Ausgabe des gemessenen Durchmessers im Command Window
Zum Beenden des Programms wird in das ursprüngliche Verzeichnis zurückgewechselt und die Webcam gestoppt.
%% Beenden
cd('/Users/madlen/Desktop/DSB/User/SoSe2018/Madlen Bartnick')
delete(cam);
Videobeweis
Als Nachweis und zur Veranschaulichung der Funktion dieses Programms dient dieses Youtube Video.
Weblinks
BSD-Lizenzbedingung BSD-Lizenz
Copyright (c) 2014, Hochschule Hamm-Lippstadt, Dep. Lip. 1, Prof. Schneider
Hochschule Hamm-Lippstadt. Alle Rechte vorbehalten.
→ zurück zum Hauptartikel: Digitale Signal- und Bildverarbeitung SoSe2018