Beschleunigungssensor mit Matlab/Simulink: Unterschied zwischen den Versionen
| (10 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 67: | Zeile 67: | ||
Auf der Hauptplatine des Sensors lässt sich neben dem Beschleunigungsmesser noch ein Microchip erkennen, in dem die gemessenen Signale vorverarbeitet werden. | Auf der Hauptplatine des Sensors lässt sich neben dem Beschleunigungsmesser noch ein Microchip erkennen, in dem die gemessenen Signale vorverarbeitet werden. | ||
Auf dem Microcontroller werden die gemessenen analogen Daten verarbeitet. Dafür kommt die im nebenstehenden Bild gezeigte vereinfachte Schaltung zum Einsatz. Die analogen Eingänge teilen sich die Verbindung mit dem digitalen Eingang, sodass | Auf dem Microcontroller werden die gemessenen analogen Daten verarbeitet. Dafür kommt die im nebenstehenden Bild gezeigte vereinfachte Schaltung zum Einsatz. Die analogen Eingänge teilen sich die Verbindung mit dem digitalen Eingang, sodass auf der Pinseite eine in Sperrrichtung vorgespannte ESD-Schutzdiode eigesetzt werden muss. Der analoge Eingang sollte daher immer zwischen den positiven Versorgungsspanungen Vss und Vdd liegen. Wenn die Eingangsspannung um mehr als 0,6 V abweicht ist eine der Dioden vorgespannt und es kann zu einem Latch up kommen. Als Latch up wird der Übergang eines Halbleiterbauelements in einen niederohmigen Zustand verstanden, der bei fehlenden Schutzmaßnahmen zu einem Kurzschluss führen kann. Für die analogen Quellen wird eine max. Quellenimpedanz von 10 kOhm empfohlen. Des Weiteren sollte jeder externen Komponente, die mit einem Eingangspin wie einem Kondensator, einen sehr geringen Leckstrom aufweisen, um die eingeführte Ungenauigkeit zu minimieren. | ||
=== Analog - Digital - Umsetzer === | === Analog - Digital - Umsetzer === | ||
| Zeile 98: | Zeile 98: | ||
Die digitale Signalverarbeitung wird sensorintern durchgeführt (wie in den vorherigen Schritten zur Signalbearbeitung erläutert) und mit Hilfe eines NXT Bricks an den PC gesendet und mit Matlab digital weiterverarbeitet. Der nebenstehende Programmablaufplan soll den Ablauf des in Matlab gestarteten Programms visualisieren. Der konkrete Matlab-Code ist im SVN-Ordner hinterlegt. | Die digitale Signalverarbeitung wird sensorintern durchgeführt (wie in den vorherigen Schritten zur Signalbearbeitung erläutert) und mit Hilfe eines NXT Bricks an den PC gesendet und mit Matlab digital weiterverarbeitet. Der nebenstehende Programmablaufplan soll den Ablauf des in Matlab gestarteten Programms visualisieren. Der konkrete Matlab-Code ist im SVN-Ordner hinterlegt. | ||
Zur Signalverarbeitung mit Matlab wurden die RWTH Toolbox verwendet und die darin enthaltenden Funktionen genutzt. Matlab sollte vorbereitet werden und alle vorherigen NXT Ports und Handlungen geschlossen werden, damit die NXT Verbindung neu aufgerufen werden kann. Der NXT-Eingang wird als | Zur Signalverarbeitung mit Matlab wurden die RWTH Toolbox verwendet und die darin enthaltenden Funktionen genutzt. Matlab sollte vorbereitet werden und alle vorherigen NXT Ports und Handlungen geschlossen werden, damit die NXT Verbindung neu aufgerufen werden kann. Der NXT-Eingang wird als global definiert und der Sensor initialisiert, indem man angibt an welchem Eingang der entsprechende Sensor am NXT Brick angeschlossen ist. In einer Schleife werden 1000 Messwerte aufgenommen und jeweils in einem Array abgespeichert und in Laufzeit ausgegeben. Nach Durchlaufen der Schleife wird der Sensoreingang und die komplette NXT Verbindung wieder geschlossen. | ||
Die mit diesem Matlab-Code gemessene Beschleunigung ist in den nebenstehenden Abbildungen gezeigt. Einmal ohne die Anwendung eines Filters und eine zweite mit Anwendung eines Tiefpass- | Die mit diesem Matlab-Code gemessene Beschleunigung ist in den nebenstehenden Abbildungen gezeigt. Einmal ohne die Anwendung eines Filters und eine zweite mit Anwendung eines Tiefpass-Filters. Die Funktion des Filters wird im Weiteren erläutert. | ||
| Zeile 128: | Zeile 128: | ||
<div class="tright" style="clear:none">[[Datei:Horizontal_Sensor_Neu.jpg|mini|ohne|x250px| Messung der Neigung bei horizontaler Anordnung des Sensors ohne Filter.]]</div> | <div class="tright" style="clear:none">[[Datei:Horizontal_Sensor_Neu.jpg|mini|ohne|x250px| Messung der Neigung bei horizontaler Anordnung des Sensors ohne Filter.]]</div> | ||
Die ausgegebenen Signale des Sensor über den NXT an das Simulationsprogramm Matlab weisen ein Rauschen auf. Der Sensor wurde dazu horizontal auf den Tisch gestellt und die Werte aufgenommen. Auf Grund des Rauschens | Die ausgegebenen Signale des Sensor über den NXT an das Simulationsprogramm Matlab weisen ein Rauschen auf. Der Sensor wurde dazu horizontal auf den Tisch gestellt und die Werte aufgenommen. Auf Grund des Rauschens wurden die Sensordaten im Weiteren mit einem Tiefpass gefiltert. | ||
Schaltungen, die auf ein frequenzunabhängiges Übertragungsverhalten ausgelegt sind, werden als Filter bezeichnet. | Schaltungen, die auf ein frequenzunabhängiges Übertragungsverhalten ausgelegt sind, werden als Filter bezeichnet. Das Eingangssignal kann so in einer gewünschten Art, je nach Filter umgeformt werden. Filter besitzen so vielfache Anwendungsmöglichkeiten in der Signalverarbeitung. Im Allgemein wird zwischen vier Grundtypen von Filtern unterschieden: der Tiefpass, Hochpass, Bandpass und der Sperrfilter. Die Filter können durch konzentrierte Bauelemente wie Spule und Kondensator realisiert werden. In unserem Fall wurde der Tiefpassfilter verwendet, um das Rauschen der Sensordaten zu minimieren. Ein Tiefpassfilter lässt alle Signalanteile mit einer Frequenz unterhalb der Grenzfrequenz passieren. Die Signalanteile oberhalb dieser Grenzfrequenz werden blockiert <ref name="Filter"> RuhrUni Bochum moodle: Filter. - Letzter Aufruf: 20.06.2018 https://moodle.ruhr-uni-bochum.de/m/mod/wiki/view.php?pageid=1236#toc-2 </ref>. | ||
Als Tiefpassfilter in Matlab wurde das Demo-Programm bzw. die Funktion "Tiefpass" von Hr. Schneider aus dem 2. Fachsemester aus der Veranstaltung "Moderne Tracking Systeme" verwendet. | Als Tiefpassfilter in Matlab wurde das Demo-Programm bzw. die Funktion "Tiefpass" von Hr. Schneider aus dem 2. Fachsemester aus der Veranstaltung "Moderne Tracking Systeme" verwendet. | ||
| Zeile 136: | Zeile 136: | ||
Als Auflösung eines Sensors wird der kleinste unterscheidbare Schritt am Ausgang also in der Anzeige bezeichnet <ref name="Auflösung"> Carl-Enger-Schule Karlsruhe(2008): Formelsammlung Messtechnik. - Letzter Aufruf: 20.06.2018 http://www.carl-engler-schule.de/culm/culm/culm2/th_messtechnik/systeme/messgrundlagen1-3.pdf </ref>. Bei unserem Sensor ist die Auflösung eine Beschleunigungsabstufung von 0,005 g, also 0,049 m/s² <ref name="Auflösung Sensor"> Berns,K. und Schmidt, D.(2010): Programmierung mit LEGO Mindstorms NXT. Springer-Verlag. - Letzter Aufruf: 20.06.2018 https://books.google.de/books?id=YR4kBAAAQBAJ&pg=PA56&lpg=PA56&dq=Funktionsweise+nxt+beschleunigungssensor&source=bl&ots=G7KNwyf9NA&sig=y42Ep4bMCVQSncs5D8zoUdmoZmw&hl=de&sa=X&ved=0ahUKEwj3zLTtqb_bAhWBLhQKHTGPC58Q6AEINjAB#v=onepage&q=Funktionsweise%20nxt%20beschleunigungssensor&f=false</ref>. Die Auflösung hängt ebenfalls vom eingesetzten AD-Wandler ab. In unserem Falle wird ein 10-Bit Wandler verwendet. Es gibt demnach 10 Binärstellen und demnach 2^10 also 1024 unterschiedlich Digitalsignale <ref name="Auflösung"> http://www.carl-engler-schule.de/culm/culm/culm2/th_messtechnik/systeme/messgrundlagen1-3.pdf </ref>. Zusätzlich wird das höherwertige Bit auf dem NXT genutzt um das Vorzeichen zu definieren. Bei einer 1 ist es negativ, bei einer | Als Auflösung eines Sensors wird der kleinste unterscheidbare Schritt am Ausgang also in der Anzeige bezeichnet <ref name="Auflösung"> Carl-Enger-Schule Karlsruhe(2008): Formelsammlung Messtechnik. - Letzter Aufruf: 20.06.2018 http://www.carl-engler-schule.de/culm/culm/culm2/th_messtechnik/systeme/messgrundlagen1-3.pdf </ref>. Bei unserem Sensor ist die Auflösung eine Beschleunigungsabstufung von 0,005 g, also 0,049 m/s² <ref name="Auflösung Sensor"> Berns,K. und Schmidt, D.(2010): Programmierung mit LEGO Mindstorms NXT. Springer-Verlag. - Letzter Aufruf: 20.06.2018 https://books.google.de/books?id=YR4kBAAAQBAJ&pg=PA56&lpg=PA56&dq=Funktionsweise+nxt+beschleunigungssensor&source=bl&ots=G7KNwyf9NA&sig=y42Ep4bMCVQSncs5D8zoUdmoZmw&hl=de&sa=X&ved=0ahUKEwj3zLTtqb_bAhWBLhQKHTGPC58Q6AEINjAB#v=onepage&q=Funktionsweise%20nxt%20beschleunigungssensor&f=false</ref>. Die Auflösung hängt ebenfalls vom eingesetzten AD-Wandler ab. In unserem Falle wird ein 10-Bit Wandler verwendet. Es gibt demnach 10 Binärstellen und demnach 2^10 also 1024 unterschiedlich Digitalsignale <ref name="Auflösung"> http://www.carl-engler-schule.de/culm/culm/culm2/th_messtechnik/systeme/messgrundlagen1-3.pdf </ref>. Zusätzlich wird das höherwertige Bit auf dem NXT genutzt um das Vorzeichen zu definieren. Bei einer 1 ist es negativ, bei einer Null bzw. wenn nichts davor steht ist es positiv. | ||
Nach DIN1319-1 ist die Empfindlichkeit eines Sensors die Änderung des Wertes der Ausgangsgröße bezogen auf die verursachende Änderung der Werte der Eingangsgröße <ref name="Empfindlichkeit"> Micro-epsilon.de: Empfindlichkeit. - Letzter Aufruf: 20.06.2018 https://www.micro-epsilon.de/service/glossar/Empfindlichkeit.htmlf </ref>. Die Empfindlichkeit des Beschleunigungssensor ist im Datenblatt angegeben. Der Sensor ist auf eine Versorgungsspannung von 3,3 V kalibriert, aber die betriebliche Stromversorgung liegt bei 2,4 bis 3,6 V. Die Empfindlichkeit ist mit einer Versorgungsspannung von 3,3 V und 25°C gemessen worden und beläuft sich auf die 3,3 V geteilt durch 5, also 0,66 | Nach DIN1319-1 ist die Empfindlichkeit eines Sensors die Änderung des Wertes der Ausgangsgröße bezogen auf die verursachende Änderung der Werte der Eingangsgröße <ref name="Empfindlichkeit"> Micro-epsilon.de: Empfindlichkeit. - Letzter Aufruf: 20.06.2018 https://www.micro-epsilon.de/service/glossar/Empfindlichkeit.htmlf </ref>. Die Empfindlichkeit des Beschleunigungssensor ist im Datenblatt angegeben. Der Sensor ist auf eine Versorgungsspannung von 3,3 V kalibriert, aber die betriebliche Stromversorgung liegt bei 2,4 bis 3,6 V. Die Empfindlichkeit ist mit einer Versorgungsspannung von 3,3 V und 25°C gemessen worden und beläuft sich auf die 3,3 V geteilt durch 5, also 0,66 bei einer Versorgungsspannung von 3,3 V. Die Empfindlichkeit hat ein Minimum und Maximum bei 0,66 +- 5 % <ref name="Datenblatt"> ST.com: Datenblatt des Beschleunigungsmessers (LIS344ALH). - Letzter Aufruf: 20.06.2018 http://www.st.com/content/ccc/resource/technical/document/datasheet/59/4c/43/66/c7/4d/4b/db/CD00182781.pdf/files/CD00182781.pdf/jcr:content/translations/en.CD00182781.pdf </ref>. | ||
| Zeile 302: | Zeile 302: | ||
=== Darstellung der Ergebnisse === | === Darstellung der Ergebnisse === | ||
In der Messtechnik werden Fehler in zufällige und systematische Fehler gegliedert. Die zufälligen Fehler lassen sich dabei durch die Messunsicherheit bzw. das Vertrauensintervall abbilden. In der Tabelle sind die Messunsicherheit und das Vertrauensintervall angegeben und es lässt sich erkennen, dass diese sich lediglich auf die dritte Nachkommastelle auswirken. Die zufälligen Fehler sind daher fast zu vernachlässigen. | In der Messtechnik werden Fehler in zufällige und systematische Fehler gegliedert. Die zufälligen Fehler lassen sich dabei durch die Messunsicherheit bzw. das Vertrauensintervall abbilden. In der Tabelle sind die Messunsicherheit und das Vertrauensintervall angegeben und es lässt sich erkennen, dass diese sich lediglich auf die dritte bzw. bei zwei Messungen auf die zweite Nachkommastelle auswirken. Die zufälligen Fehler sind daher fast zu vernachlässigen. | ||
Der systematische Fehler dagegen ist sehr groß und schwankt je nach Messart. In der oben dargestellten Tabelle sollte eigentlich bei allen Messungen ein Wert um die 200 | Der systematische Fehler dagegen ist sehr groß und schwankt je nach Messart. In der oben dargestellten Tabelle sollte eigentlich bei allen Messungen ein Wert um die 200, also die Erdbeschleunigung herauskommen. Bei den Messungen wurde lediglich die Neigung untersucht und nicht die Beschleunigung. Dafür wurde der Sensor in eine Vorrichtung gespannt und nicht bewegt. Die größte Abweichung von der eigentlichen Erdbeschleunigung beträgt 6,5 % bei einem nach unten gerichteten Sensor. | ||
[[Datei:Vertrauensintervall.jpg |mini|300px| Darstellung des Vertrauensintervalls des Sensors bei verschiedenen Messarten.]] | [[Datei:Vertrauensintervall.jpg |mini|300px| Darstellung des Vertrauensintervalls des Sensors bei verschiedenen Messarten.]] | ||
| Zeile 311: | Zeile 311: | ||
Dem NXT Brick selber wird bereits vom Sensor ein digitaler Wert übergeben, sodass auch der NXT Brick keinen so großen und unterschiedlichen systematischen Fehler verursachen kann. | Dem NXT Brick selber wird bereits vom Sensor ein digitaler Wert übergeben, sodass auch der NXT Brick keinen so großen und unterschiedlichen systematischen Fehler verursachen kann. | ||
Die Fehlerquelle des systematischen Fehlers kann daher nur in der internen Signalverarbeitung des Sensors sein. Komisch ist, dass kein gleichbleibender Fehler zu erkennen ist, sondern ein mit Änderung der Messart unterschiedlich | Die Fehlerquelle des systematischen Fehlers kann daher nur in der internen Signalverarbeitung des Sensors sein. Komisch ist, dass kein gleichbleibender Fehler zu erkennen ist, sondern ein mit Änderung der Messart unterschiedlich ausgeprägter Fehler. Durch den komplexen Aufbau des Sensors konnte dort keine Fehlerquellen gefunden werden. | ||
Die Messunsicherheit und das Vertrauensintervall bei jeder Messart wurde in der nebenstehenden Abbildung dargestellt. | Die Messunsicherheit und das Vertrauensintervall bei jeder Messart wurde in der nebenstehenden Abbildung dargestellt. | ||
| Zeile 317: | Zeile 317: | ||
== Zusammenfassung & Ausblick == | == Zusammenfassung & Ausblick == | ||
Zusammenfassend lässt sich sagen, dass der Beschleunigungssensor über NXT ausgelesen werden konnte und zur einfacheren Betrachtung die Neigung genauer untersucht wurde. Die ausgelesenen Sensordaten weisen eine sehr große Spannweite auf und es lässt sich keine Regelmäßigkeit in den gemessenen Sensordaten feststellen, die die unterschiedlichen Abweichungen bei den Messarten erklären würde. Im Weiteren könnte genauer untersucht werden, wieso sich unterschiedliche Messdaten bei den unterschiedlichen Messarten ergeben. In einem zweiten Schritt kann eine Versuchsvorrichtung gebaut werden, um für eine Beschleunigungsmessung ebenfalls Referenzdaten zu bekommen. Diese beiden Punkte wurden aus Zeitmangel nicht mehr beachtet und könnten im Nachgang noch weiter untersucht werden. | |||
== Lessons Learned == | == Lessons Learned == | ||
Aktuelle Version vom 28. Juni 2018, 21:19 Uhr
Im Rahmen der Lehrveranstaltung Signalverarbeitende Systeme im Modul Systementwurf des Masterstudienganges Business and Systems Engineering ist die Aufgabe semesterbegleitend ein Projekt mit Matlab/Lego Mindstorms zu lösen.
Autor: Julia Averesch
Aufgabenstellung

Der ausgesuchte Sensor, in diesem Fall der HiTechnics Beschleunigungssensor, soll mit Matlab/Simulink ausgelesen werden und die Signalverarbeitungskette beschrieben, untersucht und verstanden werden.
Projektplan
Eine Projektplanung wurde mit Hilfe des Programms MS Project erstellt. Hierbei wurde die Annahme getroffen, dass in Kalenderwochen gearbeitet wurde, sodass keine festen Arbeitstage feststanden, sondern innerhalb der geplanten Woche eine bestimmte Anzahl an Stunden zu einem bestimmten Thema am Projekt gearbeitet werden sollte. Die Projektplanung wurde erst ab Juni begonnen, da erste Priorität die wissenschaftliche Arbeit für das gleichnamige Modul hatte und bis Juni soweit fast fertiggestellt sein sollte. Der eigentliche Projektstart lag deswegen für mich am 1. Juni 2018.
Ich erstellte einen Projektplan für die nächsten Wochen bis zum Semesterende und entwickelte erste Ideen, wie der Beschleunigungssensor an einen PC angeschlossen werden könnte. Als Lösung wurde ein NXT Brick verwendet und dieser beschaffen. Als nächstes sollten die einzelnen Schritte zur Signalverarbeitung nacheinander abgearbeitet werden. Der letzte Schritt konnte erst nach dem Fertigstellen des Matlab-Programms beginnen. Zeitgleich mit dem Anfang der Bearbeitung der Signalverarbeitungsschritte sollte der PC für die Verbindung mit einem NXT vorbereitet werden. Danach kann begonnen werden das Matlab-Programm zum Auslesen des Sensors zu schreiben. Nachdem all diese Punkte bearbeitet worden sind, sollte begonnen werden den Wiki-Artikel zu schreiben. Daraufhin folgte der Videodreh und das Schneiden des Videos. Eine Woche nach Fertigstellung des Projektplans wurden die Termine angepasst, da eine parallele Arbeit von Wiki-Artikel und den einzelnen Signalverarbeitungsschritten als sinnvoller erschien. Zudem konnten die ersten Schritte in einer Wohche bearbeitet werden, da ich in dem Thema so vertieft war und so länger als geplant daran gearbeitet habe.
Konzepterstellung zum Auslesen des Sensors mit Matlab/Simulink
Nach der Ausgabe der Sensoren wurde festgestellt, dass der Sensor nicht so einfach an den PC angeschlossen werden kann. Der erste Ansatz war, dass der Sensor mit einem Arduino Uno ausgelesen werden sollte und eine Kommunikation zwischen PC und Arduino zu den Sensordaten führen sollte. Hierbei gestaltete sich für mich das Problem, dass das Anschlusskabel hätte auseinander geschnitten und die einzelnen Adern an den Arduino gelötet werden müssen. Da ich nicht über ausreichende Kenntnisse verfüge, wollte ich eine andere Lösungsmöglichkeit probieren. Auch der Ansatz den Sensor direkt über die Sensoreingänge des EV3 auszulesen funktionierte leider nicht, da der Beschleunigungssensor nicht im Lego Mindstorms EV3 Support Package enthalten ist. Der dritte Lösungsansatz und schließlich der hier erläuterte ist das Auslesen des Sensors mit Hilfe des älteren Lego Mindstorms NXT. Der HiTechnics Beschleunigungssensor ist in der RWTH - Mindstorms Toolbox enthalten und wird hier zum Auslesen mit Matlab verwendet.
Anleitung für den Anschluss des NXT an den eigenen Laptop
Damit der NXT an den PC angeschlossen und der Sensor ausgelesen werden kann, muss zuvor die Toolbox in Matlab eingebunden und der passende Treiber für den NXT installiert werden. Gemäß der Anleitung wurde zunächt die Toolbox in Matlab integriert. Dazu wird die Toolbox als ZIP-Datei heruntergeladen, entpackt und dann im Matlab Ordner gespeichert. Der passende Lego USB Treiber kann ebenfalls heruntergeladen werden. In der Anleitung wird der Fantom USB Treiber genannt. Doch im weiteren Verlauf stellte sich heraus, dass dieser lediglich für Windows 32-Bit Version geeignet ist. Nach umfassender Recherche benötigt ein Windows 64-Bit Betriebssystem einen libusb-Treiber, dieser kann ebenfalls auf einer Internetseite heruntergeladen werden. Unter den neueren Betriebssystemen (ab Windows 8) ist beim Installieren des Treibers das Problem, dass es sich um keinen von Microsoft signierten Treiber handelt. Die erste Möglichkeit besteht darin, den Rechner im Shutdown-Modus zu starten. Dies war mir aber zu riskant, sodass ich nach längerer Recherche auf ein Programm gestoßen bin, mit welchem sich der Treiber ohne Probleme installieren lässt.
Schritte zur Signalbearbeitung
Die Signalverarbeitungskette des Beschleunigungssensor soll beschrieben, untersucht und verstanden werden, sodass die sechs Schritte zur Signalbearbeitung in diesem Kapitel behandelt werden sollen.
Auswahl eines Primärsensors
Der ausgewählte Sensor für dieses Projekt ist ein Beschleunigungssensor der Firma HiTechnics. Dieser trägt die offizielle Bezeichnung NXT Acceleration/Tilt Sensor (NAC 1040) und wurde für den Lego Mindstorms NXT entwickelt [1].
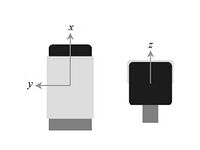
Der Sensor misst die Beschleunigung in drei Achsen (X, Y und Z) und kann zudem noch die Neigung entlang der Achse ermitteln.
Die Beschleunigung wird mit einer Skalierung von ca. 200 Zählimpulsen pro g in einem Bereich von -2 g bis +2 g gemessen. Die Beschleunigungsmessung wird für jede Achse etwa 100 mal pro Sekunde aktualisiert. Die Neigung der drei Achsen kann ebenfalls gemessen werden, da die Schwerkraft als Beschleunigung wahrgenommen wird. Ist der Sensor stationär und in normaler horizontaler Position so sind die X- und Y- Achsen fast null, da der Sensor horizontal steht. Die Z-Achse dagegen sollte bei einem Wert von 200 liegen, was der Erdbeschleunigung 1 g entspricht. Wird der Sensor geneigt, so wird die Schwerkraft auch auf den anderen Achsen erkannt und der Wert für die Z-Achse beginnt zu sinken. Die Schwerkraft wird so auf drei Komponentenvektoren verteilt und die Neigung des Sensors kann bestimmt werden.
So ist dieser Sensor auch für selbstnivellierende Roboter geeeignet, da der Sensor anzeigt, ob der Roboter gerade steht. [1]

Sieht man sich den Sensor von innen an, so lässt sich die Hauptplatine des NAC 1040 erkennen. Auf der Hauptplatine ist ein 20-poliger Microchip (PIC16F677) und eine 3-Achsen-MEMS-Beschleunigungsmesser (STMicroelectronics LIS344ALH). Das graue Gehäuse ist die Buchse für den Anschluss des NXT Roboters [2].
Der 20-polige Microship ist ein Flash-basierter 8-Bit-CMOS Microcontroller mit NanoWatt-Technologie. Das Datenblatt ist hier zu finden.

Im nachfolgenden wird der Beschleunigungsmesser detaillierter analysiert. Der Beschleunigungsmesser ist in die Gruppe der MEMS-Bauelemente einzuordnen, die elektronische und mechanische Bauteile auf winzigen Bauraum vereinen. Ein entsprechendes Datenblatt ist hier zu finden. Der Beschleunigungsmesser besteht aus einem Sensorelement und einer IC-Schnittstelle, die in der Lage ist, die Informationen der Messung in ein analoges Signal für die Außenwelt umzuwandeln. Der 4 x 4 mm große Beschleunigungsmesser enthält zwei drahtgebundene Siliziumchips. Der obere Chip beinhaltet den anwendungsspezifischen integrierten Schaltkreis für die Signalverarbeitung (ASIC). Der untere Chip wiederum besteht aus zwei Chips, dem MEMS-Chip und dem hermetischen Kappenchip [2].

Das Werkzeuglayout des MEMS-Chip, welches durch reaktives Ionentiefenätzen erstellt wurde ist im nebenstehenden Bild zu sehen. Es lassen sich zwei mikrobearbeitete Strukturen erkennen, die eine 3-Achsen-Beschleunigungserfassung ermöglichen. Die linke Struktur ist empfindlich für Bewegungen in der XY-Ebene der Matrize und die rechte Struktur für Z-Bewegungen senkrecht zur Matrizenoberfläche. Wenn nun eine Beschleunigung auf den Sensor ausgeübt wird, verschiebt sich die Prüfmasse „Proof Mass“ von ihrer eigentlichen Position und verursacht ein Ungleichgewicht in der kapazitiven Halbbrücke. Dieses Ungleichgewicht wird unter Verwendung der Ladungsintegration als Reaktion auf einen an den Erfassungskondensator angelegten Spannungsimpuls gemessen. Im stationären Zustand beträgt der Nennwert der Kondensatoren wenige pikofarad. Wenn eine Beschleunigung anliegt ist die kapazitive Last im femtofarad Bereich [2].
Der Sensor liefert digitale Rohwerte, sodass das eigentlich analoge Signal, wie oben beschrieben, noch durch den Microship vorverarbeitet wird. Der Sensor arbeitet in einem Bereich von ±19,62 m/s². Es können also, wie oben schon genannt Beschleunigungen in Höhe der doppelten Erdbeschleunigung gemessen werden. Die Erdbeschleunigung g entspricht dabei den Rohwert 200 vom Sensor.
Signalvorbereitung
Der Beschleunigungsmesser hat eine IC-Schnittstelle über den die analogen Daten an den Microchip übergeben werden. Zunächst wird ein rauscharmer kapazitiver Verstärker eingesetzt, der eine korrelierte Doppelabtastung (CDS) am Ausgang implementiert. Dadurch hebt sich der Offset und das Rauschen auf. Das erzeugte Signal wird dann an drei verschiedene Sample and Holds gesendet, so dass das Signal nach außen verfügbar gemacht wird. Die IC-Schnittstelle ist werkseitig auf Empfindlichkeit und Null-Pegel kalibriert. Die nötigen Abgleichwerte werden im Gerät selber durch eine nichtflüchtige Struktur gespeichert. Bei jedem Einschalten des Gerätese werden die Parameter in das Register geladen, sodass der Benutzer diesen Sensor ohne weitere Kalibrierung verwenden kann.
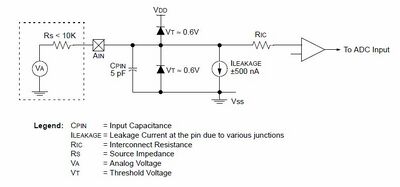
Auf der Hauptplatine des Sensors lässt sich neben dem Beschleunigungsmesser noch ein Microchip erkennen, in dem die gemessenen Signale vorverarbeitet werden.
Auf dem Microcontroller werden die gemessenen analogen Daten verarbeitet. Dafür kommt die im nebenstehenden Bild gezeigte vereinfachte Schaltung zum Einsatz. Die analogen Eingänge teilen sich die Verbindung mit dem digitalen Eingang, sodass auf der Pinseite eine in Sperrrichtung vorgespannte ESD-Schutzdiode eigesetzt werden muss. Der analoge Eingang sollte daher immer zwischen den positiven Versorgungsspanungen Vss und Vdd liegen. Wenn die Eingangsspannung um mehr als 0,6 V abweicht ist eine der Dioden vorgespannt und es kann zu einem Latch up kommen. Als Latch up wird der Übergang eines Halbleiterbauelements in einen niederohmigen Zustand verstanden, der bei fehlenden Schutzmaßnahmen zu einem Kurzschluss führen kann. Für die analogen Quellen wird eine max. Quellenimpedanz von 10 kOhm empfohlen. Des Weiteren sollte jeder externen Komponente, die mit einem Eingangspin wie einem Kondensator, einen sehr geringen Leckstrom aufweisen, um die eingeführte Ungenauigkeit zu minimieren.
Analog - Digital - Umsetzer
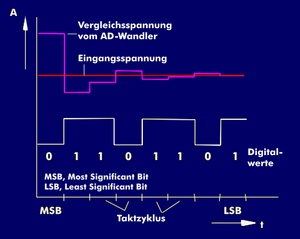
Der Analog-Digital Wandler sitzt im Mikrochip und ermöglicht die Umwandlung eines analogen Eingangssignal von der IC Schnittstelle des Beschleunigungsmesser in eine 10-Bit Binärdarstellung. Der Wandler verwendet analoge Eingänge, die in einer einzigen Abtast- und Halteschaltung gemultiplext werden, um Resourcen zu sparen. Durch sukzessive Approximaion wird ein 10-Bit Binärergebnis gespeichert und in den ADC-Ergebnisregistern gespeichert (ADRESL und ADRESH).
Unter einer sukzessiven Approximation wird eine schrittweise Annäherung verstanden. Das bedeutet, dass die analoge Eingangsspannung mit einer Referenzspannung schrittweise verglichen wird. Dieser Vergleich wiederholt sich ständig und die Referenzspannung wird in jedem Schritt so geändert, dass sie immer näher an der Eingangsspannung ist. Vorstellen kann man es sich wie eine alte Waage mit Gewichten, weswegen das Verfahren auch Wägeverfahren genannt wird. In der nebenstehenden Abbildung ist das Prinzip dieses Verfahrens dargestellt. Wenn die Vergleichsspannung höher ist als die Eingangsspannung, dann wird das Most Significant BIT auf den Lo-Wert 0 gesetzt. Andersherum auf den Hi-Wert 1 und die Referenzspannung wird halbiert. Dies wird so lange gemacht bis alle Bits gesetzt sind. Das letzte Bit wird Least Significant Bit genannt. Dieser Analog-Digital Umsetzer ist sehr leicht ohne großen Aufwand zu realisieren im Gegensatz zum Flash-Umsetzer [4].
Bussystem
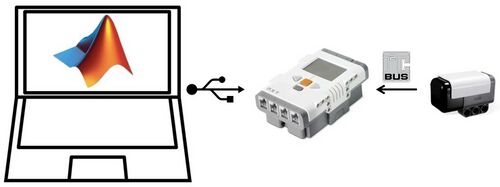
Zwischen dem Sensor und dem Mikrocontroller, hier dem NXT-Lego Mindstorms wird ein Bussystem das sogenannte I²C eingesetzt. 1982 wurde I²C von Phillips als Kommunikationsbus entwickelt und der Lego NXT Baustein verwendet dieses. Das bedeutet, dass jede Kommunikation zwischen NXT Brick und dem Beschleunigungssensor über das I²C Protokoll übertragen wird und so eine einfache und effiziente Kommunikation zwischen Mikrocontroller und Sensoren gewährleistet ist.
Dieses Bussystem funktioniert nach dem Master Slave Prinzip. Dabei ist der NXT Brick der Master und der Beschleunigungssensor der Slave. Die Übertragung zwischen Master und Slave beginnt mit einem Start Bit und endet mit einem Stop Bit. Zwischen diesen beiden Bits findet die eigentliche Übertragung statt. Dabei schreibt zunächst der Master (NXT Brick), die I²C-Schnittstelle des Slaves (Sensors) in den Bus. Die beiden Bausteine können jetzt ihre Daten austauschen und durch ein vom Master gesendetes Stop Bit wieder angehalten werden [5].
Damit der NXT Brick an den PC angeschlossen werden kann und mit Matlab ausgelesen kann wird ein serielles Bus-System verwendet (USB). Hierbei werden einzelne Bits nacheinander übertragen. Dabei enthält jedes Bit ein Teil der Informationen, die übertragen werden sollen.
Digitale Signalverarbeitung
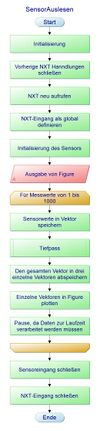
Die digitale Signalverarbeitung wird sensorintern durchgeführt (wie in den vorherigen Schritten zur Signalbearbeitung erläutert) und mit Hilfe eines NXT Bricks an den PC gesendet und mit Matlab digital weiterverarbeitet. Der nebenstehende Programmablaufplan soll den Ablauf des in Matlab gestarteten Programms visualisieren. Der konkrete Matlab-Code ist im SVN-Ordner hinterlegt.
Zur Signalverarbeitung mit Matlab wurden die RWTH Toolbox verwendet und die darin enthaltenden Funktionen genutzt. Matlab sollte vorbereitet werden und alle vorherigen NXT Ports und Handlungen geschlossen werden, damit die NXT Verbindung neu aufgerufen werden kann. Der NXT-Eingang wird als global definiert und der Sensor initialisiert, indem man angibt an welchem Eingang der entsprechende Sensor am NXT Brick angeschlossen ist. In einer Schleife werden 1000 Messwerte aufgenommen und jeweils in einem Array abgespeichert und in Laufzeit ausgegeben. Nach Durchlaufen der Schleife wird der Sensoreingang und die komplette NXT Verbindung wieder geschlossen.
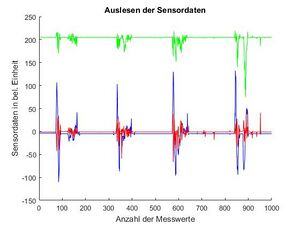
Die mit diesem Matlab-Code gemessene Beschleunigung ist in den nebenstehenden Abbildungen gezeigt. Einmal ohne die Anwendung eines Filters und eine zweite mit Anwendung eines Tiefpass-Filters. Die Funktion des Filters wird im Weiteren erläutert.

Die ausgegebenen Signale des Sensor über den NXT an das Simulationsprogramm Matlab weisen ein Rauschen auf. Der Sensor wurde dazu horizontal auf den Tisch gestellt und die Werte aufgenommen. Auf Grund des Rauschens wurden die Sensordaten im Weiteren mit einem Tiefpass gefiltert.
Schaltungen, die auf ein frequenzunabhängiges Übertragungsverhalten ausgelegt sind, werden als Filter bezeichnet. Das Eingangssignal kann so in einer gewünschten Art, je nach Filter umgeformt werden. Filter besitzen so vielfache Anwendungsmöglichkeiten in der Signalverarbeitung. Im Allgemein wird zwischen vier Grundtypen von Filtern unterschieden: der Tiefpass, Hochpass, Bandpass und der Sperrfilter. Die Filter können durch konzentrierte Bauelemente wie Spule und Kondensator realisiert werden. In unserem Fall wurde der Tiefpassfilter verwendet, um das Rauschen der Sensordaten zu minimieren. Ein Tiefpassfilter lässt alle Signalanteile mit einer Frequenz unterhalb der Grenzfrequenz passieren. Die Signalanteile oberhalb dieser Grenzfrequenz werden blockiert [6].
Als Tiefpassfilter in Matlab wurde das Demo-Programm bzw. die Funktion "Tiefpass" von Hr. Schneider aus dem 2. Fachsemester aus der Veranstaltung "Moderne Tracking Systeme" verwendet.
Als Auflösung eines Sensors wird der kleinste unterscheidbare Schritt am Ausgang also in der Anzeige bezeichnet [7]. Bei unserem Sensor ist die Auflösung eine Beschleunigungsabstufung von 0,005 g, also 0,049 m/s² [8]. Die Auflösung hängt ebenfalls vom eingesetzten AD-Wandler ab. In unserem Falle wird ein 10-Bit Wandler verwendet. Es gibt demnach 10 Binärstellen und demnach 2^10 also 1024 unterschiedlich Digitalsignale [7]. Zusätzlich wird das höherwertige Bit auf dem NXT genutzt um das Vorzeichen zu definieren. Bei einer 1 ist es negativ, bei einer Null bzw. wenn nichts davor steht ist es positiv.
Nach DIN1319-1 ist die Empfindlichkeit eines Sensors die Änderung des Wertes der Ausgangsgröße bezogen auf die verursachende Änderung der Werte der Eingangsgröße [9]. Die Empfindlichkeit des Beschleunigungssensor ist im Datenblatt angegeben. Der Sensor ist auf eine Versorgungsspannung von 3,3 V kalibriert, aber die betriebliche Stromversorgung liegt bei 2,4 bis 3,6 V. Die Empfindlichkeit ist mit einer Versorgungsspannung von 3,3 V und 25°C gemessen worden und beläuft sich auf die 3,3 V geteilt durch 5, also 0,66 bei einer Versorgungsspannung von 3,3 V. Die Empfindlichkeit hat ein Minimum und Maximum bei 0,66 +- 5 % [10].
Die Messunsicherheit des Sensors ist die halbe Breite des Vertrauensbereichs und wird durch folgende Formel
(1)
beschrieben. Dabei ist t ein Zahlenfaktor in Abhängigkeit von der Anzahl der Messwerte n und dem gewählten Vertrauensniveau. In der Technik wird meist ein Vertrauensbereich von 95 % gewählt, welches einem t von 1,96 bei 1000 Messwerten entspricht. Des Weiteren wird die Standardabweichung s zur Berechnung der Messunsicherheit benötigt. Aus der Messunsicherheit kann das Vertrauensintervall abgeleitet werden [11]. Die Messunsicherheit und das Vertrauensintervall wurde für jeden Neigungswinkel separat bestimmt. Hierbei wurde auf die Neigungsmessung eingegangen, da bei dieser der Referenzwert der Erdbeschleunigung gegeben ist und nicht auf die Beschleunigungsmessung, da dort die Referenzdaten fehlen.
Wird der arithmetische Mittelwert mit dem eigentlichen Mittelwert verglichen, so ist eine Abweichung zu erkennen, die bei jeder Messung unterschiedlich und teilweise relativ hoch ist. Aus diesem Grund wurde ebenfalls die relative und absolute Messabweichung ermittelt. Die Messunsicherheit und das Vertrauensintervall bezieht sich daher nur auf den gemessenen Wert und nicht auf den eigentlichen wahren Wert. Die erkannte Abweichung ist ein Hinweis auf einen systematischen Fehler in der Messung.
Darstellung der Ergebnisse
In der Messtechnik werden Fehler in zufällige und systematische Fehler gegliedert. Die zufälligen Fehler lassen sich dabei durch die Messunsicherheit bzw. das Vertrauensintervall abbilden. In der Tabelle sind die Messunsicherheit und das Vertrauensintervall angegeben und es lässt sich erkennen, dass diese sich lediglich auf die dritte bzw. bei zwei Messungen auf die zweite Nachkommastelle auswirken. Die zufälligen Fehler sind daher fast zu vernachlässigen. Der systematische Fehler dagegen ist sehr groß und schwankt je nach Messart. In der oben dargestellten Tabelle sollte eigentlich bei allen Messungen ein Wert um die 200, also die Erdbeschleunigung herauskommen. Bei den Messungen wurde lediglich die Neigung untersucht und nicht die Beschleunigung. Dafür wurde der Sensor in eine Vorrichtung gespannt und nicht bewegt. Die größte Abweichung von der eigentlichen Erdbeschleunigung beträgt 6,5 % bei einem nach unten gerichteten Sensor.

Auf dem NXT Brick können ebenfalls die Sensorwerte ausgelesen werden. Diese stimmten bei den Messungen mit denen in Matlab generierten Werte überein. Dies lässt vermuten, dass in diesem Verarbeitungsschritt kein systematischer Fehler zu finden ist, es könnte sich lediglich um einen kleinen zufälligen Fehler handeln.
Dem NXT Brick selber wird bereits vom Sensor ein digitaler Wert übergeben, sodass auch der NXT Brick keinen so großen und unterschiedlichen systematischen Fehler verursachen kann.
Die Fehlerquelle des systematischen Fehlers kann daher nur in der internen Signalverarbeitung des Sensors sein. Komisch ist, dass kein gleichbleibender Fehler zu erkennen ist, sondern ein mit Änderung der Messart unterschiedlich ausgeprägter Fehler. Durch den komplexen Aufbau des Sensors konnte dort keine Fehlerquellen gefunden werden.
Die Messunsicherheit und das Vertrauensintervall bei jeder Messart wurde in der nebenstehenden Abbildung dargestellt.
Zusammenfassung & Ausblick
Zusammenfassend lässt sich sagen, dass der Beschleunigungssensor über NXT ausgelesen werden konnte und zur einfacheren Betrachtung die Neigung genauer untersucht wurde. Die ausgelesenen Sensordaten weisen eine sehr große Spannweite auf und es lässt sich keine Regelmäßigkeit in den gemessenen Sensordaten feststellen, die die unterschiedlichen Abweichungen bei den Messarten erklären würde. Im Weiteren könnte genauer untersucht werden, wieso sich unterschiedliche Messdaten bei den unterschiedlichen Messarten ergeben. In einem zweiten Schritt kann eine Versuchsvorrichtung gebaut werden, um für eine Beschleunigungsmessung ebenfalls Referenzdaten zu bekommen. Diese beiden Punkte wurden aus Zeitmangel nicht mehr beachtet und könnten im Nachgang noch weiter untersucht werden.
Lessons Learned
Der Projektplan musste nach einer Woche noch einmals sehr stark angepasst werden, da doch längere Zeit am Sensor gearbeitet wurde und so schon viel in einem kürzeren Zeitraum, allerdings bei gleichem Zeitaufwand, geschafft werden konnte. Ebenfalls war zu erst geplant, die einzelnen Schritte der Signalbearbeitung zu bearbeiten und erst im Nachhinein alles in einen Wiki-Artikel zusammenzufassen. Dieser Plan wurde auch bereits in der ersten Woche verworfen und bereits zeitgleich alles in einem Wiki-Artikel zusammengefasst.
YouTube Video
Beschleunigungssensor mit Matlab/Simulink
Datenblätter
Beschleunigungsmesser: Datei:LIS344ALH.pdf
Microchip des Sensors(leider ist das pdf zu groß zum hochladen)
Weiterleitung zum Projektordner in SVN
Die Projektdaten sind in diesem SVN-Verzeichnis zu finden.
Literatur
- ↑ 1,0 1,1 1,2 1,3 Modernroboticsins.com: HiTechnic NXT Acceleration/Tilt Sensor. - Letzter Aufruf: 20.06.2018 http://modernroboticsinc.com/hitechnic-nxt-acceleration-tilt-sensor Sensor Referenzfehler: Ungültiges
<ref>-Tag. Der Name „HiTechnics Acceleration/Tilt Sensor“ wurde mehrere Male mit einem unterschiedlichen Inhalt definiert. - ↑ 2,0 2,1 2,2 2,3 2,4 2,5 findmems.com: Tearing down LEGO MINDSTORMS® – STMicroelectronics MEMS accelerometer LIS344ALH. - Letzter Aufruf: 20.06.2018 http://www.findmems.com/stmicroelectronics/tearing-down-lego-mindstorms%C2%AE-stmicroelectronics-mems-accelerometer-lis344alh Referenzfehler: Ungültiges
<ref>-Tag. Der Name „Innenleben Sensor“ wurde mehrere Male mit einem unterschiedlichen Inhalt definiert. - ↑ Datenblatt des Microchips (PIC16F677). - Letzter Aufruf: 20.06.2018 http://ww1.microchip.com/downloads/en/DeviceDoc/41262d.pdf
- ↑ 4,0 4,1 itwissen.info: SAR (successive approximation register) - Letzter Aufruf: 20.06.2018 https://www.itwissen.info/SAR-successive-approximation-register-SAR-Verfahren.html
- ↑ generationrobots.com: Analyse des I2C Buses mit einem Logikanalysator mit Lego Mindstorms. - Letzter Aufruf: 20.06.2018 https://www.generationrobots.com/blog/de/2017/01/analyse-des-i2c-buses-mit-einem-logikanalysator-mit-lego-mindstorms/
- ↑ RuhrUni Bochum moodle: Filter. - Letzter Aufruf: 20.06.2018 https://moodle.ruhr-uni-bochum.de/m/mod/wiki/view.php?pageid=1236#toc-2
- ↑ 7,0 7,1 Carl-Enger-Schule Karlsruhe(2008): Formelsammlung Messtechnik. - Letzter Aufruf: 20.06.2018 http://www.carl-engler-schule.de/culm/culm/culm2/th_messtechnik/systeme/messgrundlagen1-3.pdf Referenzfehler: Ungültiges
<ref>-Tag. Der Name „Auflösung“ wurde mehrere Male mit einem unterschiedlichen Inhalt definiert. - ↑ Berns,K. und Schmidt, D.(2010): Programmierung mit LEGO Mindstorms NXT. Springer-Verlag. - Letzter Aufruf: 20.06.2018 https://books.google.de/books?id=YR4kBAAAQBAJ&pg=PA56&lpg=PA56&dq=Funktionsweise+nxt+beschleunigungssensor&source=bl&ots=G7KNwyf9NA&sig=y42Ep4bMCVQSncs5D8zoUdmoZmw&hl=de&sa=X&ved=0ahUKEwj3zLTtqb_bAhWBLhQKHTGPC58Q6AEINjAB#v=onepage&q=Funktionsweise%20nxt%20beschleunigungssensor&f=false
- ↑ Micro-epsilon.de: Empfindlichkeit. - Letzter Aufruf: 20.06.2018 https://www.micro-epsilon.de/service/glossar/Empfindlichkeit.htmlf
- ↑ ST.com: Datenblatt des Beschleunigungsmessers (LIS344ALH). - Letzter Aufruf: 20.06.2018 http://www.st.com/content/ccc/resource/technical/document/datasheet/59/4c/43/66/c7/4d/4b/db/CD00182781.pdf/files/CD00182781.pdf/jcr:content/translations/en.CD00182781.pdf
- ↑ "Papula, Lothar: Mathematische Formelsammlung - für Ingenieure und Naturwissenschaftler. [10. Auflage] Wiesbaden: Vieweg + Teubner, 2009.
→ zurück zum Hauptartikel: Signalverarbeitende Systeme








