Gewichtsgeregelte Flüssigkeitsdosierung: Unterschied zwischen den Versionen
| (31 dazwischenliegende Versionen von 3 Benutzern werden nicht angezeigt) | |||
| Zeile 16: | Zeile 16: | ||
= Anforderungen = | = Anforderungen = | ||
Im vorliegenden Abschnitt werden die essenziellen Anforderungen des Projekts systematisch dargelegt. Die erste Tabelle enthält detaillierte Angaben zu Hardware, Software und Dokumentationsanforderungen. In der zweiten Tabelle wird das erforderliche Material gemäß dem Bedarfsnachweis aufgeführt. | |||
{| class="wikitable" | {| class="wikitable" | ||
|+ Tabelle 1: Anforderungsliste | |+ Tabelle 1: Anforderungsliste | ||
| Zeile 144: | Zeile 148: | ||
Werte unterschieden werden. Das bedeutet, dass die theoretisch kleinste messbare Gewichtsänderung<br><br> | Werte unterschieden werden. Das bedeutet, dass die theoretisch kleinste messbare Gewichtsänderung<br><br> | ||
<math>m_{LSB}=\frac{1\,\text{kg}}{2.362.232}\approx 4{,}23\cdot 10^{-7}\,\text{kg}=0{,423}\,\text{mg}</math><br><br> | <math>m_{LSB}=\frac{1\,\text{kg}}{2.362.232}\approx 4{,}23\cdot 10^{-7}\,\text{kg}=0{,423}\,\text{mg}</math><br><br> | ||
beträgt, was aufgrund von Messrauschen, Vibration (z.B. in Folge der Schrittmotorbewegung), Temperatur- oder sonstigen Umwelteinflüssen in der Praxis nicht erreicht werden kann. | beträgt, was aufgrund von Messrauschen, Vibration (z.B. in Folge der Schrittmotorbewegung), Temperatur- oder sonstigen Umwelteinflüssen in der Praxis nicht erreicht werden kann.<br><br> | ||
Die Empfindlichkeit des Sensors beschreibt das Verhältnis von Ausgangssignal zu Eingangssignal. Bei diesem Aufbau ist das Ausgangssignal die verstärkte Spannung von <math>704\,\text{mV}</math> und das Eingangssignal das Gewicht von <math>1\,\text{kg}</math>, was zu einer Empfindlichkeit von:<br><br> | |||
<math>E=\frac{0{,}704\,\text{V}}{1\,\text{kg}}=0{,}704\,\frac{\text{V}}{\text{kg}}</math><br><br> | |||
führt. Da der Zusammenhang zwischen der Ausgangsspannung der Brückenschaltung und des Gewichts linear ist, gilt diese Empfindlichkeit für den gesamten Messbereich. | |||
=== Serielle Schnittstelle === | === Serielle Schnittstelle === | ||
| Zeile 283: | Zeile 290: | ||
<br> | <br> | ||
[[Datei:Umsetzung des Projektaufbaus.jpg|thumb|none|400px|Abbildung 12: reale Umsetzung der Konstruktion]] | [[Datei:Umsetzung des Projektaufbaus.jpg|thumb|none|400px|Abbildung 12: reale Umsetzung der Konstruktion]] | ||
Weitere Konstruktionsdateien sind jederzeit zugänglich im SVN der HSHL hinterlegt. | Weitere Konstruktionsdateien sind jederzeit zugänglich im [https://svn.hshl.de/svn/Elektrotechnik_Fachpraktikum/trunk/Projekte/151-175/170_Gewichtsgeregelte_Fluessigkeitsdosierung/Konstruktion SVN] der HSHL hinterlegt. | ||
<br><br> | <br><br> | ||
Der Deckel des Gehäuses, lässt sich ein Stück abheben, wodurch ein direkter Zugang zu den Anschlüssen des Arduinos möglich ist. Außerdem lässt sich nun die eingebaute Tür des Gehäuses öffnen. So kann einfach an die innenliegenden Bauteile gelangt werden. | Der Deckel des Gehäuses, lässt sich ein Stück abheben, wodurch ein direkter Zugang zu den Anschlüssen des Arduinos möglich ist. Außerdem lässt sich nun die eingebaute Tür des Gehäuses öffnen. So kann einfach an die innenliegenden Bauteile gelangt werden. | ||
| Zeile 292: | Zeile 299: | ||
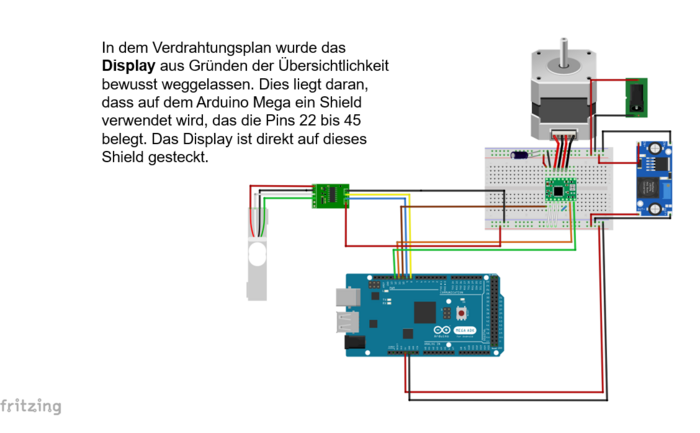
In folgender Abbildung ist der Verdrahtungsplan zu sehen: | In folgender Abbildung ist der Verdrahtungsplan zu sehen: | ||
<br> | |||
<div><ul> | |||
<li style="display: inline-block;"> [[Datei:Verdrahtungsplan_1.png |thumb|none|700px|Abbildung 13: Verdrahtungsplan mit Fritzing ]] </li> | |||
</ul></div> | |||
== Software == | == Software == | ||
[[Datei:PAP_Flüssigkeitsdosierung.png|thumb|right|305px|Abbildung | [[Datei:PAP_Flüssigkeitsdosierung.png|thumb|right|305px|Abbildung 14: Programmablaufplan Flüssigkeitsdosierung]] | ||
Die Umsetzung der Software für den Mikrocontroller erfolgt in MATLAB/Simulink. Sie besteht aus den wesentlichen Bestandteilen | Die Umsetzung der Software für den Mikrocontroller erfolgt in MATLAB/Simulink. Sie besteht aus den wesentlichen Bestandteilen | ||
| Zeile 450: | Zeile 459: | ||
=== Regler === | === Regler === | ||
Zur Implementierung und Auslegung des Reglers wird zunächst ein Modell der Regelstrecke, also des Systems erstellt. Dieses Modell wird experimentell ermittelt, indem ein Sollwertsprung der Motorgeschwindigkeit in <math>\left[ \text{Steps/s}\right]</math> eingeleitet wird: | Zur Implementierung und Auslegung des Reglers wird zunächst ein Modell der Regelstrecke, also des Systems erstellt. Dieses Modell wird experimentell ermittelt, indem ein Sollwertsprung der Motorgeschwindigkeit in <math>\left[ \text{Steps/s}\right]</math> eingeleitet wird: | ||
[[Datei:Sprungantwort.png|thumb|none| | [[Datei:Sprungantwort.png|thumb|none|600px|Abbildung 15: Sprungantwort der Regelstrecke]] | ||
Nach ca. 145 Sekunden wurde das Experiment abgebrochen, da das I-Verhalten dieses Systems eindeutig ist. | Nach ca. 145 Sekunden wurde das Experiment abgebrochen, da das I-Verhalten dieses Systems eindeutig ist. | ||
<br> | <br> | ||
Aus der ermittelten Regelstrecke und den weiteren Komponenten dieses Projektes ergibt sich folgender Regelkreis: | Aus der ermittelten Regelstrecke und den weiteren Komponenten dieses Projektes ergibt sich folgender Regelkreis: | ||
[[Datei:Regelkreis P Regler .png|thumb|none|900px|Abbildung | [[Datei:Regelkreis P Regler .png|thumb|none|900px|Abbildung 16: Regelkreis]] | ||
<br> | <br> | ||
Um die richtige Reglerart zu bestimmen, welche nötig ist, um eine bleibende Regelabweichung zu verhindern und dennoch den statischen Endwert erreicht, wird die Führungsübertragungsfunktion des geschlossenen Regelkreises für einen P-Regler betrachtet:<br><br> | Um die richtige Reglerart zu bestimmen, welche nötig ist, um eine bleibende Regelabweichung zu verhindern und dennoch den statischen Endwert erreicht, wird die Führungsübertragungsfunktion des geschlossenen Regelkreises für einen P-Regler betrachtet:<br><br> | ||
| Zeile 468: | Zeile 477: | ||
Diese Übertragungsfunktion erreicht den statischen Endwert: | Diese Übertragungsfunktion erreicht den statischen Endwert: | ||
<br><br><math>x_{stat}=\lim_{{s \to 0}}G_{WP}=\frac{k_P\cdot k_I}{0+k_P\cdot k_I}=1 </math><br><br> | <br><br><math>x_{stat}=\lim_{{s \to 0}}G_{WP}=\frac{k_P\cdot k_I}{0+k_P\cdot k_I}=1 </math><br><br> | ||
Hiermit ist bewiesen, dass ein einfacher P-Regler für unsere Zwecke ausreichend ist.<br><br> | |||
'''Reglerauslegung'''<br><br> | |||
Zur Auslegung des Reglers wird zunächst ein separates Simulink-Modell zur reinen Simulation des Regelkreises erstellt. | Zur Auslegung des Reglers wird zunächst ein separates Simulink-Modell zur reinen Simulation des Regelkreises erstellt. | ||
Hier wird durch verschiedene Einstellungen des Verstärkungsfaktors <math>K_P</math> das gewünschte Regelverhalten angenähert. Dabei wird beachtet, dass der Regler nicht zu früh die Geschwindigkeit reduziert, da dies den Befüllungsprozess unnötig in die Länge ziehen würde. Andererseits darf die Geschwindigkeit auch nicht zu spät reduziert werden. Dies hätte ein ungenaueres Dosieren zur Folge. Folgend sind die Simulationsergebnisse für verschiedene <math> | Hier wird durch verschiedene Einstellungen des Verstärkungsfaktors <math>K_P</math> das gewünschte Regelverhalten angenähert. Dabei wird beachtet, dass der Regler nicht zu früh die Geschwindigkeit reduziert, da dies den Befüllungsprozess unnötig in die Länge ziehen würde. Andererseits darf die Geschwindigkeit auch nicht zu spät reduziert werden. Dies hätte ein ungenaueres Dosieren zur Folge. Folgend sind die Simulationsergebnisse für verschiedene <math>k_P</math> dargestellt: | ||
[[Datei:Reglerauslegung P Regler.png|thumb|none|1000px|Abbildung | [[Datei:Reglerauslegung P Regler.png|thumb|none|1000px|Abbildung 17: Simulationsergebnisse Reglerauslegung]] | ||
<br> | |||
Hieraus lässt sich schon erkennen, dass <math>k_P=100 \frac{\text{Steps}}{\text{s}\cdot \text{g}}</math> für das reale System nicht sinnvoll wäre, da der Regler sehr früh beginnt die Drehzahl zu verringern und das Befüllen sehr lange dauert. | |||
<br> | <br> | ||
Nach erster Annäherung wird das Führungsübertragungsverhalten am realen System getestet und feinjustiert. So wird nach einigen Messungen ein Verstärkungsfaktor von: | Nach erster Annäherung wird das Führungsübertragungsverhalten am realen System getestet und feinjustiert. So wird nach einigen Messungen ein Verstärkungsfaktor von: | ||
<br><br><math> | <br><br><math>k_P=1500 \frac{\text{Steps}}{\text{s}\cdot \text{g}}</math><br><br> | ||
festgelegt. Der P-Regler genügt also den Anforderungen und wird vollständig in Simulink umgesetzt. Das Subsystem sieht in Simulink folgendermaßen aus:<br> | festgelegt. Dieser erweist sich als hoch genug, um nicht zu viel Zeit zu verlieren und regelt trotzdem sehr genau. | ||
[[Datei:Implementierung P-Regler.png|thumb|none|600px|Abbildung | <br> Der P-Regler genügt also den Anforderungen und wird vollständig in Simulink umgesetzt. Das Subsystem für die Reglerimplementierung sieht in Simulink folgendermaßen aus:<br> | ||
[[Datei:Implementierung P-Regler.png|thumb|none|600px|Abbildung 18: Implementierung P-Regler in Simulink]] | |||
<br> | <br> | ||
| Zeile 572: | Zeile 585: | ||
<br><br> | <br><br> | ||
<div><ul> | <div><ul> | ||
<li style="display: inline-block;"> [[Datei:WDHGenauigkeit KPG.png|thumb|none|700px|Abbildung | <li style="display: inline-block;"> [[Datei:WDHGenauigkeit KPG.png|thumb|none|700px|Abbildung 19: Test der Wiederholgenauigkeit]] </li> | ||
</ul></div> | </ul></div> | ||
| Zeile 580: | Zeile 593: | ||
<br><br> | <br><br> | ||
<div><ul> | <div><ul> | ||
<li style="display: inline-block;"> [[Datei:Fig000 KPG.png|thumb|none|700px|Abbildung | <li style="display: inline-block;"> [[Datei:Fig000 KPG.png|thumb|none|700px|Abbildung 20: Statische Messung ohne Auflagegewicht]] </li> | ||
</ul></div> | </ul></div> | ||
| Zeile 586: | Zeile 599: | ||
<div><ul> | <div><ul> | ||
<li style="display: inline-block;"> [[Datei:Fig361 KPG.png|thumb|none|700px|Abbildung | <li style="display: inline-block;"> [[Datei:Fig361 KPG.png|thumb|none|700px|Abbildung 21: Statische Messung mit einem Auflagegewicht von <math>\approx 361\,\text{g}</math>]] </li> | ||
</ul></div> | </ul></div> | ||
<div><ul> | <div><ul> | ||
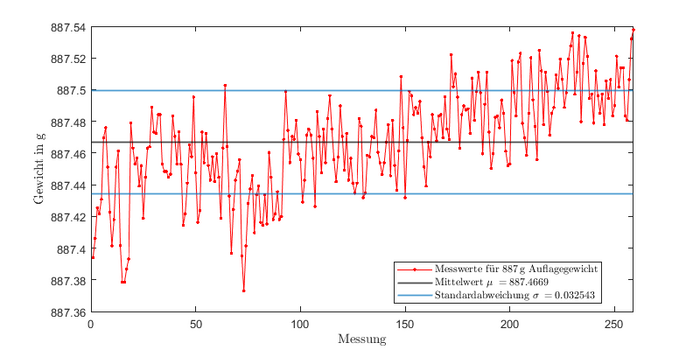
<li style="display: inline-block;"> [[Datei:Fig887 KPG.png|thumb|none|700px|Abbildung | <li style="display: inline-block;"> [[Datei:Fig887 KPG.png|thumb|none|700px|Abbildung 22: Statische Messung mit einem Auflagegewicht von <math>\approx 887\,\text{g}</math>]] </li> | ||
</ul></div> | </ul></div> | ||
Da das genaue Gewicht in beiden Fällen nicht auf Nachkommastellen bekannt ist, kann hier keine Aussage bezüglich der Abweichung des Mittelwerts von dem tatsächlichen Wert getroffen werden. Jedoch ist klar erkennbar, dass die Standardabweichungen in beiden Fällen ähnlich gering sind, wie bei der Messung ohne Auflagegewicht. Bei der Messung in Abbildung | Da das genaue Gewicht in beiden Fällen nicht auf Nachkommastellen bekannt ist, kann hier keine Aussage bezüglich der Abweichung des Mittelwerts von dem tatsächlichen Wert getroffen werden. Jedoch ist klar erkennbar, dass die Standardabweichungen in beiden Fällen ähnlich gering sind, wie bei der Messung ohne Auflagegewicht. Bei der Messung in Abbildung 22 ist am Ende ein leichter Trend "nach oben" zu erkennen, der sich allerdings im Milligrammbereich befindet. Alles in allem lässt sich festhalten, dass die Stabilität des Sensors hervorragend ist. | ||
<br><br> | |||
Für die Messunsicherheit nach GUM (Guide to the Expression of Uncertainty in Measurement)<ref>[https://www.ptb.de/cms/fileadmin/internet/fachabteilungen/abteilung_8/8.4_mathematische_modellierung/277_PTB_SEMINAR/VORTRAEGE/11_Mieke_-_Berechnung_der_Messunsicherheit_nach_GUM__Kurzfassung_in_20.pdf Berechnung der Messunsicherheit nach GUM]</ref> werden für die Wägezelle die statische Messung mit <math>361\,\text{g}</math> sowie die Angaben in dessen Datenblatt genutzt werden. Für die Messunsicherheit Typ A ergeben sich die in der Legende der Abbildung 21 angegebenen Werte für den empirischen Mittelwert und die empirische Standardabweichung. Die Standardunsicherheit nach Typ A berechnet sich dann zu:<br><br> | |||
<math>u_A=\frac{t\left( n-1\right)}{\sqrt{n}}\cdot s</math><br><br> | |||
mit<br><br> | |||
<math>t(n-1) = 2{,}0188</math>: Vertrauensfaktor der Student-t-Verteilung<br> | |||
<math>n = 180</math>: Anzahl Messungen<br> | |||
<math>s\approx 0{,}027592\,\text{g}</math>: Empirische Standardabweichung<br><br> | |||
Der Vertrauensfaktor der Student-t-Verteilung wurde mit der MATLAB Statistics Toolbox berechnet. Es ergibt sich:<br><br> | |||
<math>u_A=\frac{2{,}0188}{\sqrt{180}}\cdot 0{,}027592\,\text{g}=\pm 0{,}0042\,\text{g}</math><br><br> | |||
Im Datenblatt<ref>[https://www.roboter-bausatz.de/media/pdf/9b/2f/5b/Datenblatt-W-gezelle-1-20kg.pdf Datenblatt Wägezelle]</ref> finden sich folgende Angaben, die zur Messunsicherheit Typ B führen:<br><br> | |||
*Nichtlinearität: <math>0{,}05\,\%</math> des Messbereichs<br> | |||
*Verzögerung: <math>0{,}05\,\%</math> des Messbereichs<br> | |||
*Wiederholgenauigkeit: <math>0{,}05\,\%</math> des Messbereichs<br><br> | |||
Was zur Messunsicherheit Typ B führt:<br><br> | |||
<math>u_B=\sqrt{u_{NL}^2 + u_{VZ}^2 + u_{WD}^2}</math><br><br> | |||
mit<br><br> | |||
<math>u_{NL}</math>: Anteil der Messunsicherheit durch Nichtlinearität<br> | |||
<math>u_{VZ}</math>: Anteil der Messunsicherheit durch Verzögerung<br> | |||
<math>u_{WD}</math>: Anteil der Messunsicherheit durch Wiederholgenauigkeit<br><br> | |||
Für den Messbereich von <math>1000\,\text{g}</math> und mit Dezimalwerten, statt Prozentwerten, ergibt sich:<br><br> | |||
<math>u_B=\sqrt{\left( \frac{1000\,\text{g}\cdot 0{,}0005}{\sqrt{3}}\right)^2 + \left( \frac{1000\,\text{g}\cdot 0{,}0005}{\sqrt{3}}\right)^2 + \left( \frac{1000\,\text{g}\cdot 0{,}0005}{\sqrt{3}}\right)^2}=\pm 0{,}5\,\text{g}</math><br><br> | |||
Für die Unsicherheiten der drei Einflussgrößen wird jeweils eine Gleichverteilung angenommen, weshalb die Anteile jeweils noch durch <math>\sqrt{3}</math> geteilt werden. Die Messunsicherheit Typ C berechnet sich aus der Wurzel der Summe der Quadrate aus Typ A und Typ B:<br><br> | |||
<math>u_C=\sqrt{u_{A}^2 + u_{B}^2}=\sqrt{(0{,}0042\,\text{g})^2 + (0{,}5\,\text{g})^2}\approx \pm 0{,}5\,\text{g}</math>,<br><br> | |||
welche noch mit dem Vertrauensfaktor <math>k=2</math> für das Vertrauensniveau von <math>95,5\,\%</math> zur erweiterten Messunsicherheit verrechnet werden kann:<br><br> | |||
<math>u_E=k\cdot u_C=2\cdot\pm 0{,}5\,\text{g}=\pm 1\,\text{g}</math><br><br> | |||
Dieses Ergebnis lässt sich so interpretieren, dass bei <math>95,5\,\%</math> aller Messungen der Messwert garantiert nicht weiter als <math>\pm 1\,\text{g}</math> abweicht. Dies erfüllt unsere Anforderungen an die Genauigkeit exakt. | |||
== Regler == | == Regler == | ||
| Zeile 617: | Zeile 656: | ||
| align="center" style="background:#4472C4; color:white"|'''Kommentar''' | | align="center" style="background:#4472C4; color:white"|'''Kommentar''' | ||
|- | |- | ||
| align="center" | 18 || align="center" | Regelbetrieb || align="center" | 005, 013 || align="center" | Regeldifferenz = <math>5\,\text{g}</math> || align="center" | Simulink-Testumgebung starten durch Klick auf "Run" || align="center" | Die Stellgröße beträgt <math>5\,\text{g}\cdot 1500\,\frac{\text{Steps}}{\text{s}\cdot \text{g}}=7500\,\frac{\text{Steps}}{\text{s}}</math> || align="center" | Stellgröße <math>= 7500\,\frac{\text{Steps}}{\text{s}}</math> || align="center" style="background:#008000; color:white" | Erfolgreich || | | align="center" | 18 || align="center" | Regelbetrieb || align="center" | 005, 013, 014 || align="center" | Regeldifferenz = <math>5\,\text{g}</math> || align="center" | Simulink-Testumgebung starten durch Klick auf "Run" || align="center" | Die Stellgröße beträgt <math>5\,\text{g}\cdot 1500\,\frac{\text{Steps}}{\text{s}\cdot \text{g}}=7500\,\frac{\text{Steps}}{\text{s}}</math> || align="center" | Stellgröße <math>= 7500\,\frac{\text{Steps}}{\text{s}}</math> || align="center" style="background:#008000; color:white" | Erfolgreich || | ||
|- | |- | ||
| align="center" | 19 || align="center" | Stellgrößenbegrenzung 1 || align="center" | 005, 013 || align="center" | Regeldifferenz = <math>10\,\text{g}</math>, sodass Stellgröße <math>> 12.000\,\frac{\text{Steps}}{\text{s}}</math> wird || align="center" | Simulink-Testumgebung starten durch Klick auf "Run" || align="center" | Die Stellgröße wird auf die Maximalgeschwindigkeit von <math>12.000\,\frac{\text{Steps}}{\text{s}}</math> begrenzt || align="center" | Stellgröße <math>= 12.000\,\frac{\text{Steps}}{\text{s}}</math> || align="center" style="background:#008000; color:white" | Erfolgreich || | | align="center" | 19 || align="center" | Stellgrößenbegrenzung 1 || align="center" | 005, 013, 014 || align="center" | Regeldifferenz = <math>10\,\text{g}</math>, sodass Stellgröße <math>> 12.000\,\frac{\text{Steps}}{\text{s}}</math> wird || align="center" | Simulink-Testumgebung starten durch Klick auf "Run" || align="center" | Die Stellgröße wird auf die Maximalgeschwindigkeit von <math>12.000\,\frac{\text{Steps}}{\text{s}}</math> begrenzt || align="center" | Stellgröße <math>= 12.000\,\frac{\text{Steps}}{\text{s}}</math> || align="center" style="background:#008000; color:white" | Erfolgreich || | ||
|- | |- | ||
| align="center" | 20 || align="center" | Stellgrößenbegrenzung 2 || align="center" | 005, 013 || align="center" | Regeldifferenz = <math>0{,}5\,\text{g}</math>, sodass Stellgröße <math>< 1500\,\frac{\text{Steps}}{\text{s}}</math> wird || align="center" | Simulink-Testumgebung starten durch Klick auf "Run" || align="center" | Die Stellgröße wird auf die Minimalgeschwindigkeit von <math>1500\,\frac{\text{Steps}}{\text{s}}</math> begrenzt || align="center" | Stellgröße <math>= 1500\,\frac{\text{Steps}}{\text{s}}</math> || align="center" style="background:#008000; color:white" | Erfolgreich || Ein Unterschreiten dieser Geschwindigkeit kann ggf. zum Stillstand des Motors führen, obwohl das Zielgewicht noch nicht erreicht wurde. | | align="center" | 20 || align="center" | Stellgrößenbegrenzung 2 || align="center" | 005, 013, 014 || align="center" | Regeldifferenz = <math>0{,}5\,\text{g}</math>, sodass Stellgröße <math>< 1500\,\frac{\text{Steps}}{\text{s}}</math> wird || align="center" | Simulink-Testumgebung starten durch Klick auf "Run" || align="center" | Die Stellgröße wird auf die Minimalgeschwindigkeit von <math>1500\,\frac{\text{Steps}}{\text{s}}</math> begrenzt || align="center" | Stellgröße <math>= 1500\,\frac{\text{Steps}}{\text{s}}</math> || align="center" style="background:#008000; color:white" | Erfolgreich || Ein Unterschreiten dieser Geschwindigkeit kann ggf. zum Stillstand des Motors führen, obwohl das Zielgewicht noch nicht erreicht wurde. | ||
|} | |} | ||
== Pumpenansteuerung == | == Pumpenansteuerung == | ||
'''Eingänge''' | '''Eingänge'''<br> | ||
Geschwindigkeit in <math>\left[ \frac{\text{Steps}}{\text{s}}\right]</math> | |||
{| class="wikitable" | {| class="wikitable" | ||
| Zeile 643: | Zeile 679: | ||
| align="center" style="background:#4472C4; color:white"|'''Kommentar''' | | align="center" style="background:#4472C4; color:white"|'''Kommentar''' | ||
|- | |- | ||
| align="center" | 21 || align="center" | Sollgeschwindigkeit setzen || align="center" | | | align="center" | 21 || align="center" | Sollgeschwindigkeit setzen || align="center" | 003, 013 || align="center" | || align="center" | Geschwindigkeit <math>5000\,\frac{\text{Steps}}{\text{s}}</math> setzen || align="center" | Pumpe läuft || align="center" | Pumpe läuft || align="center" style="background:#008000; color:white" | Erfolgreich || | ||
|- | |- | ||
| align="center" | 22 || align="center" | Min. Sollgeschwindigkeit testen || align="center" | | | align="center" | 22 || align="center" | Min. Sollgeschwindigkeit testen || align="center" | 003, 013 || align="center" | || align="center" | Geschwindigkeit <math><5000\,\frac{\text{Steps}}{\text{s}}</math> setzen || align="center" | Pumpe pumpt nur minimal Flüssigkeit|| align="center" | minimale Sollgeschwindigkeit von <math>1500\,\frac{\text{Steps}}{\text{s}}</math> || align="center" style="background:#008000; color:white" | Erfolgreich || | ||
|- | |- | ||
| align="center" | 23 || align="center" | Max. Sollgeschwindigkeit testen || align="center" | | | align="center" | 23 || align="center" | Max. Sollgeschwindigkeit testen || align="center" | 003, 013 || align="center" | || align="center" | Geschwindigkeit <math>>5000\,\frac{\text{Steps}}{\text{s}}</math> setzen || align="center" | Pumpe pumpt möglichst schnell|| align="center" | maximale Sollgeschwindigkeit von <math>12.000\,\frac{\text{Steps}}{\text{s}}</math> || align="center" style="background:#008000; color:white" | Erfolgreich || | ||
|- | |- | ||
| align="center" | 24 || align="center" | Sollgeschwindigkeit mittels Regler || align="center" | | | align="center" | 24 || align="center" | Sollgeschwindigkeit mittels Regler || align="center" | 003, 013 || align="center" | Regler und Messung funktionieren || align="center" | Geschwindigkeit durch Regler setzen || align="center" | Pumpe pumpt mit vorgegebener Geschwindigkeit, anfangs schnell, gegen stat. Endwert hin langsamer|| align="center" | Pumpe pumpt mit vorgegebener Geschwindigkeit, anfangs schnell, gegen stat. Endwert hin langsamer || align="center" style="background:#008000; color:white" | Erfolgreich || Dieser Test wurde erst nach Zusammenbau getestet, da mehrere Komponenten mit einwirken. | ||
|- | |- | ||
| align="center" | 25 || align="center" | | | align="center" | 25 || align="center" | Stopp bei geringer Regeldifferenz || align="center" | 003, 013 || align="center" | Regler und Messung funktionieren || align="center" | Grenze Regeldifferenz setzen || align="center" | Motorstop bei erreichter Grenze|| align="center" | Motor stoppt || align="center" style="background:#008000; color:white" | Erfolgreich || Der Regler stoppt die Pumpe automatisch. Die eingestellte Grenze wird lediglich zur Begrenzung der minimalen Sollgeschwindigkeit genutzt. | ||
|- | |- | ||
| align="center" | 26 || align="center" | Pumpenrichtung || align="center" | 003 || align="center" | Flüssigkeitsbehälter inkl. Verschlauchung vorhanden || align="center" | Dir-Pin = "Low" || align="center" | Flüssigkeit wird in das Gefäß auf der Wägezelle gepumpt.|| align="center" | Flüssigkeit wird in das Gefäß auf der Wägezelle gepumpt.|| align="center" style="background:#008000; color:white" | Erfolgreich || | | align="center" | 26 || align="center" | Pumpenrichtung || align="center" | 003, 013 || align="center" | Flüssigkeitsbehälter inkl. Verschlauchung vorhanden || align="center" | Dir-Pin = "Low" || align="center" | Flüssigkeit wird in das Gefäß auf der Wägezelle gepumpt.|| align="center" | Flüssigkeit wird in das Gefäß auf der Wägezelle gepumpt.|| align="center" style="background:#008000; color:white" | Erfolgreich || | ||
|- | |- | ||
|} | |} | ||
| Zeile 664: | Zeile 700: | ||
<div><ul> | <div><ul> | ||
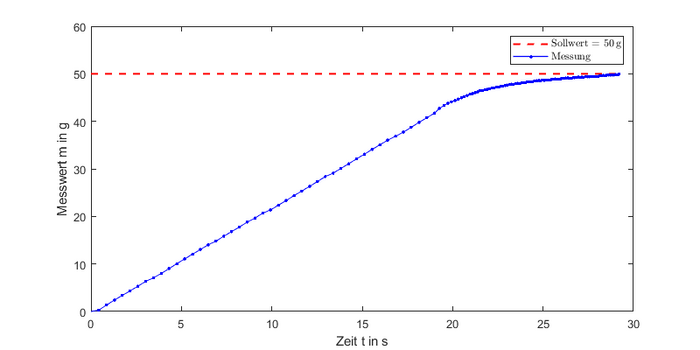
<li style="display: inline-block;"> [[Datei:Reg50 KPG.png |thumb|none|700px|Abbildung | <li style="display: inline-block;"> [[Datei:Reg50 KPG.png |thumb|none|700px|Abbildung 23: Ergebnis für Wasser mit Sollwert = <math>50\,\text{g}</math>]] </li> | ||
</ul></div> | </ul></div> | ||
| Zeile 670: | Zeile 706: | ||
<div><ul> | <div><ul> | ||
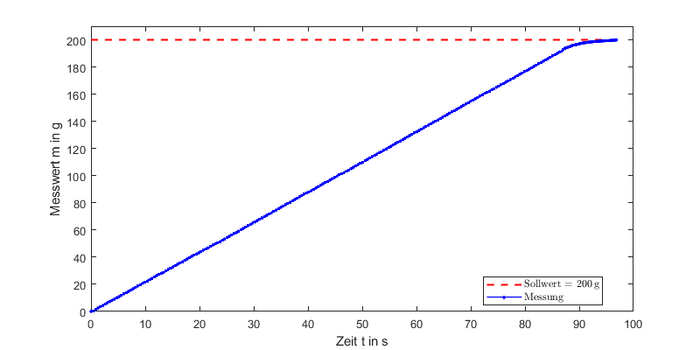
<li style="display: inline-block;"> [[Datei:Reg200 KPG.png |thumb|none|700px|Abbildung | <li style="display: inline-block;"> [[Datei:Reg200 KPG.png |thumb|none|700px|Abbildung 24: Ergebnis für Wasser mit Sollwert = <math>200\,\text{g}</math>]] </li> | ||
</ul></div> | </ul></div> | ||
| Zeile 676: | Zeile 712: | ||
<div><ul> | <div><ul> | ||
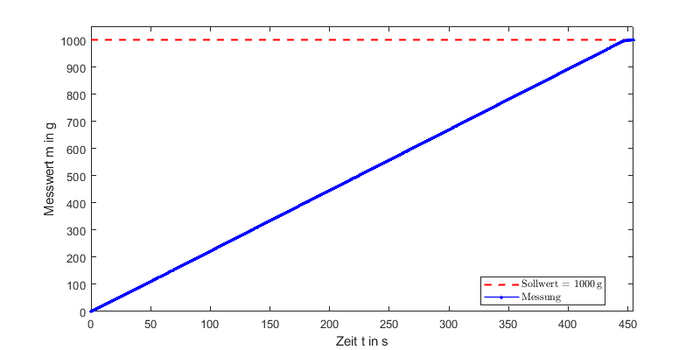
<li style="display: inline-block;"> [[Datei:Reg1000 KPG.png |thumb|none|700px|Abbildung | <li style="display: inline-block;"> [[Datei:Reg1000 KPG.png |thumb|none|700px|Abbildung 25: Ergebnis für Wasser mit Sollwert = <math>1000\,\text{g}</math>]] </li> | ||
</ul></div> | </ul></div> | ||
| Zeile 686: | Zeile 722: | ||
<div><ul> | <div><ul> | ||
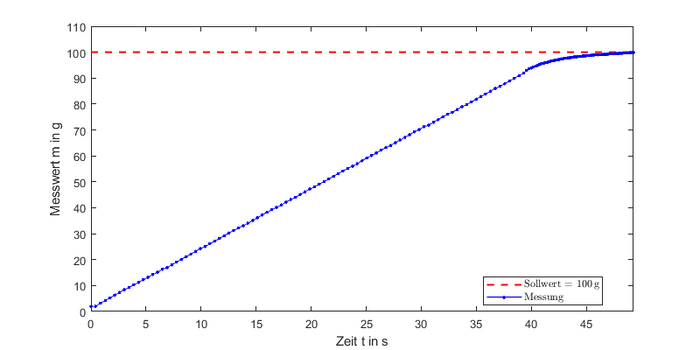
<li style="display: inline-block;"> [[Datei:Reg100 Milch KPG.png |thumb|none|700px|Abbildung | <li style="display: inline-block;"> [[Datei:Reg100 Milch KPG.png |thumb|none|700px|Abbildung 26: Ergebnis für Milch mit Sollwert = <math>100\,\text{g}</math>]] </li> | ||
</ul></div> | </ul></div> | ||
| Zeile 724: | Zeile 760: | ||
= Projektunterlagen = | = Projektunterlagen = | ||
Die relevanten Projektunterlagen wie das Gesamtmodell, die Testumgebungen etc. finden sich im ZIP-Archiv zum Download: [[Datei:Fluessigkeitsdosierung.zip]]. | |||
== Projektplan == | == Projektplan == | ||
[[Datei: BSE_GC.png| | In Abbildung 27 ist die Gantt-Chart zur Visualisierung der Aufgaben und Meilensteine dargestellt, während Abbildung 28 den Ressourcenplan zeigt. | ||
[[Datei: BSE_GC.png|1000px|thumb|left| Abb. 27: Projektplan]] | |||
<br clear = all> | |||
[[Datei:BSE_RD.png|1000px|thumb|left| Abb. 28: Ressourcenplanung]] | |||
<br clear = all> | |||
== Projektdurchführung == | == Projektdurchführung == | ||
{| class="wikitable" | |||
|+ Tabelle 10: Projektdurchführung | |||
| align="center" style="background:#4472C4; color:white"|'''Nummer''' | |||
| align="center" style="background:#4472C4; color:white"|'''Herausforderung''' | |||
| align="center" style="background:#4472C4; color:white"|'''Lösung''' | |||
|- | |||
| 1 || Projektfindung || Ideensammlung, Brainstorming: <br>automatische Müllsortierung verworfen <br>Idee einer Pumpanwendung festgelegt, da verschiedene interessante Komponenten nutzbar sind | |||
|- | |||
| 2 || Projektplan || Planung der Durchführung des Projektes, Erstellung Gantt-Diagramm | |||
|- | |||
| 3 || Anforderungen festlegen || Entscheidung zur Wägezelle und Peristaltikpumpe, Implementierung eines Reglers | |||
|- | |||
| 4 || Entwurf || Verwirklichung der Idee in technischem und funktionalem Systementwurf | |||
|- | |||
| 5 || Organisation/Auswahl benötigter Bauteile || Bestellung Peristaltikpumpe, Wägezelle, HX711 24bit ADU <br>Touchdisplay, Arduino, Kunststoffschlauch bereits vorhanden | |||
|- | |||
| 6 || Hardwareentwicklung || Konstruktion mittels CAD, u.A. Anordnung der Komponenten, Platzbedarf, Verdrahtungsplan | |||
|- | |||
| 7 || Softwareentwicklung || Komponentenspezifikationen, Programmablaufplan | |||
|- | |||
| 8 || Hardwareumsetzung || Fertigung Holzgehäuse, 3D-Druck (FDM), Lackierung <br>Verkabelung, Löten, Zusammenbau | |||
|- | |||
| 9 || Softwareumsetzung|| Programmierung einzelner Komponenten, Reglerauslegung, Erstellung Gesamtmodell | |||
|- | |||
| 10 || Tests || Komponententests, Kalibrierungstests, Genauigkeitstests, Test Gesamtprojekt | |||
|- | |||
| 11 || Dokumentation || Videodreh, Plakaterstellung, Dokumentation hier im Wiki | |||
|- | |||
|} | |||
= YouTube Video = | = YouTube Video = | ||
{{#ev:youtube|https://www.youtube.com/watch?v=cpASNc_5M20| 650 |left|'''Video vom Projekt: Gewichtsgeregelte Flüssigkeitsdosierung '''}} | {{#ev:youtube|https://www.youtube.com/watch?v=cpASNc_5M20| 650 |left|'''Video vom Projekt: Gewichtsgeregelte Flüssigkeitsdosierung '''}} | ||
<br clear=all> | <br clear=all> | ||
= Literatur = | = Literatur = | ||
Aktuelle Version vom 17. Januar 2024, 19:45 Uhr
Autor: Asmaa Kachout Aarourou & Daniel Gosedopp & Florian Pichmann
Betreuer: Marc Ebmeyer
Einleitung
Im Studiengang Business and Systems Engineering wird im Rahmen des Fachpraktikums "Angewandte Elektrotechnik" ein Gruppenprojekt entwickelt.
Dieses Projekt befasst sich mit einer gewichtsgeregelten Flüssigkeitsdosierung, die für Anwendungen mit grammgenauen Gewichtsanforderungen verwendet werden kann. Als Beispiel kann hier die Chemieindustrie bei der Abfüllung von Reinigungs-/Pflegeprodukten oder das Mixen von Nährstofflösungen für Pflanzen genannt werden. Auch der Einsatz in Schulen zur Durchführung von Experimenten mit Flüssigkeiten ist möglich.
Der Automat soll eine gewünschte Flüssigkeitsmenge mittels einer Pumpe und Schlauchverbindungen aus einem Tank in ein bereitstehendes Gefäß einfüllen. Die Sollmengenvorgabe wird mit einem Touchscreen realisiert. Hier kann entweder direkt das Gewicht oder die bekannte Dichte der Flüssigkeit zusammen mit dem gewünschten Volumen in z.B. Milliliter vorgegeben werden. Der Regelkreis wird mithilfe einer Wägezelle als Sensor, auf der das Zielbehältnis platziert wird, und einer Peristaltikpumpe (Schlauchpumpe) als Aktuator realisiert. Die Software (Signalverarbeitung, Regler) läuft auf einem Mikrocontroller. Die Vorgehensweise bei der Bearbeitung des Projekts orientiert sich am V-Modell, weshalb auch dieser Wiki-Artikel in die Phasen des V-Modells bis zum Komponententest gegliedert ist.
Insgesamt besteht das Projekt aus den drei Hauptteilen Hardwareaufbau, Software für Signalverarbeitung und Regler sowie Software für das Touchdisplay. Die Arbeitsaufteilung innerhalb der Gruppe erfolgt an diesen Teilen.
Anforderungen
Im vorliegenden Abschnitt werden die essenziellen Anforderungen des Projekts systematisch dargelegt. Die erste Tabelle enthält detaillierte Angaben zu Hardware, Software und Dokumentationsanforderungen. In der zweiten Tabelle wird das erforderliche Material gemäß dem Bedarfsnachweis aufgeführt.
| ID | Typ (I = Info, A = Anforderung) | Kapitel | Inhalt | Ersteller | Datum | Geprüft von | Datum |
|---|---|---|---|---|---|---|---|
| 001 | I | 1 | Hardware | ||||
| 002 | A | Es muss eine Wägezelle verbaut werden, welche in der Lage ist, die Flüssigkeitsmenge mit einer Genauigkeit von +/- 1g zu messen. | Pichmann | 05.10.2023 | Kachout, Gosedopp | 06.10.2023 | |
| 003 | A | Es wird eine regelbare Peristaltikpumpe (Schlauchpumpe) verbaut. | Pichmann | 05.10.2023 | Kachout, Gosedopp | 06.10.2023 | |
| 004 | A | Zur Sollwertvorgabe wird ein Touchdisplay verwendet (HMI). Hier kann entweder ein gewünschtes Gewicht oder die Dichte der Flüssigkeit zusammen mit dem gewünschten Volumen angegeben werden. | Pichmann | 05.10.2023 | Kachout, Gosedopp | 06.10.2023 | |
| 005 | A | Für die Daten- und Signalverarbeitung, die Regelung und die Anbindung des Touchdisplays wird ein Arduino Mikrocontroller genutzt. | Pichmann | 05.10.2023 | Kachout, Gosedopp | 06.10.2023 | |
| 006 | A | Es müssen zwei Behälter (z.B. Becherglas) vorhanden sein. Einer dient als Vorrat, der Andere als Zielgefäß. | Pichmann | 05.10.2023 | Kachout, Gosedopp | 06.10.2023 | |
| 007 | A | Der Transport der Flüssigkeit zwischen den Behältern erfolgt durch Kunststoffschlauchverbindungen. | Pichmann | 05.10.2023 | Kachout, Gosedopp | 06.10.2023 | |
| 008 | A | Die Energieversorgung wird von einem externen Netzteil übernommen. Dieses muss genug Leistung haben, um die gesamte Elektronik zu betreiben. | Pichmann | 05.10.2023 | Kachout, Gosedopp | 06.10.2023 | |
| 009 | I | 2 | Software | ||||
| 010 | A | Für die Erstellung der Software wird Matlab/Simulink verwendet. Ggf. wird aus dem Modell C-Code generiert, welcher auf den Arduino geflasht wird. | Pichmann | 05.10.2023 | Kachout, Gosedopp | 06.10.2023 | |
| 011 | A | Die Software muss die Eingabe auf dem Touchdisplay zu einem Sollwert für die Regelung verarbeiten. | Pichmann | 05.10.2023 | Kachout, Gosedopp | 06.10.2023 | |
| 012 | A | Es muss ein Kalibriermodus für die Wägezelle vorhanden sein. Die Kalibrierung wird ebenfalls mit Hilfe des Touchscreens vorgenommen. Hierzu ist ein Kalibriergewicht notwendig. | Pichmann | 05.10.2023 | Kachout, Gosedopp | 06.10.2023 | |
| 013 | A | Das gemessene Ist-Gewicht wird mit dem Sollwert zu einer Regeldifferenz verrechnet, sodass der Regler eine Stellgröße zur Ansteuerung der Pumpe berechnen kann. | Pichmann | 05.10.2023 | Kachout, Gosedopp | 06.10.2023 | |
| 014 | A | Es wird ein stetiger Regler verwendet. | Pichmann | 05.10.2023 | Kachout, Gosedopp | 06.10.2023 | |
| 015 | I | 3 | Dokumentation | ||||
| 016 | A | Alle Projektdateien werden in SVN hinterlegt. | Pichmann | 05.10.2023 | Kachout, Gosedopp | 06.10.2023 | |
| 017 | A | Das gesamte Projekt wird im Wiki dokumentiert. | Pichmann | 05.10.2023 | Kachout, Gosedopp | 06.10.2023 |
| Anzahl | Komponente | Preis | Bestelldatum | Eingangsdatum |
|---|---|---|---|---|
| 1 | Kamoer KCM Peristaltikpumpe | 50,38€ | 20.10.2023 | 26.10.2023 |
| 1 | Arduino Mega 2560 | (vorhanden) | - | - |
| 1 | Wägezelle RBS15855 | 1,95€ | 20.10.2023 | 25.10.2023 |
| 1 | HX711 24 Bit ADU | 0,89€ | 20.10.2023 | 25.10.2023 |
| 1 | Touchdisplay | (vorhanden) | - | - |
| 1m | Kunststoffschlauch 6mm | (vorhanden) | - | - |
Funktionaler Systementwurf/Technischer Systementwurf
Um das Projekt möglichst kompakt und gleichzeitig funktionstüchtig zu gestalten, werden nach einem Brainstorming und weiterer Ideensammlung die folgenden Entwürfe erstellt. Die Hauptkomponente bildet ein Gehäuse in dem sich die Peristaltikpumpe und sämtliche Elektronik befinden soll. Das Touchdisplay für die Benutzereingaben wird leicht zugänglich am Gehäuse montiert. Die Flüssigkeit wird aus einem größerem Gefäß hinter dem Gehäuse, durch das Gehäuse in einen kleineren Behälter vor dem Gehäuse gepumpt. Dieser steht auf der Wägezelle, welche das aktuelle Gewicht ermittelt.
Komponentenspezifikation
Die erforderlichen Komponenten und ihre Spezifikation sind in diesem Abschnitt detailliert beschrieben.
Wägezelle- & Messtechnik
Primärsensor & Signalanpassung
Die genutzten Formeln und Erläuterungen im folgenden Abschnitt beruhen auf der Quelle [1], konkret den Seiten 73 und 83 - 87.
Als Primärsensor kommt ein Dehnungsmessstreifen (kurz: DMS) zum Einsatz. Dieser beruht auf dem dehnungsresistiven Effekt. Hierbei kommt es in Folge mechanischer Ausdehnung zu einer Änderung des elektrischen Widerstands eines Leiters durch Einwirken der zu messenden mechanischen Größe. Letztere ist in unserem Fall eine Gewichtskraft. Im Hook’schen Bereich des Leitermaterials gilt für die Steigung k der Hook’schen Geraden:
Fehler beim Parsen (Syntaxfehler): {\displaystyle k=\frac{\Delta R/R}{\Delta l/l}}
Für die Widerstandsänderung in Folge einer Dehnung ergibt sich demnach:
Hierbei ist ein Dehnfaktor, der materialabhängig und einem Datenblatt zu entnehmen ist. ist der Basiswiderstand des DMS im ungedehnten Zustand. ist die Gesamtlänge des Leiters und die Änderung der Leiterlänge in Folge der Dehnung . Die Widerstandsänderungen sind im Verhältnis zum Basiswiderstand des DMS sehr gering, weshalb auch die Spannungsänderungen an den DMS gering sind. Daher ist die Verschaltung eines/mehrere DMS in Brückenschaltung notwendig. Die Schaltung an der in diesem Projekt verwendeten Wägezelle besteht aus vier DMS, die zu einer Vollbrücke aufgebaut sind. Die DMS sind paarweise so angeordnet, dass sich ihre Empfindlichkeitsrichtungen gegenüberstehen. Auf der Wägezelle sieht das wie in Abbildung 3 dargestellt aus.
Gemessen wird die Potentialdifferenz zwischen Knoten 2 und 3 aus Abbildung 3 (Schaltung rechts), welche sich mit der Formel
Fehler beim Parsen (Syntaxfehler): {\displaystyle U_a=\left( \frac{R_2}{R_1+R_2}-\:\frac{R_4}{R_3+R_4}\right)\cdot U_e}
berechnet, Wobei die Brückenspeisespannung konstant ist. Wie bereits beschrieben, sollen sich die Empfindlichkeitsausrichtungen gegenüberstehen, was im Falle der Vollbrücke bedeutet
und
Werden diese Zusammenhänge in die obige Gleichung eingesetzt, so vereinfacht sich diese zu
Es handelt sich also um einen linearen Zusammenhang zwischen der Ausgangsspannung und der Widerstandsänderung. Laut Datenblatt des Sensors beträgt die Ausgangsempfindlichkeit bei maximaler Belastung der Wägezelle. Die genutzt Versorgungsspannung beträgt in unserem Fall , was für die maximale Ausgangsspannungsänderung einen Bereich von
ergibt. Die Vollbrückenschaltung liefert also immernoch sehr kleine Ausgangsspannungswerte, weshalb eine Verstärkerschaltung benötigt wird. Ein HX711 Breakout-Board ist speziell für Wägezellen entwickelt worden und beinhaltet einen programmierbaren Verstärker, einen 24-Bit Analog-Digital-Wandler, eine Digitalschnittstelle und weitere Komponenten (siehe Abbildung 4).
-
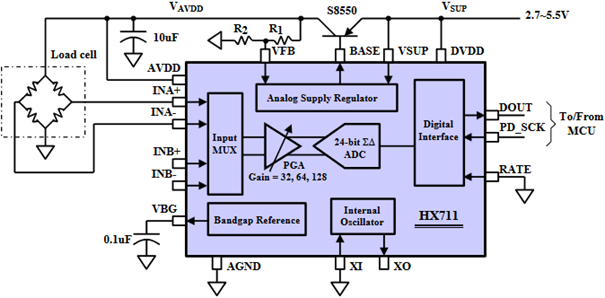
Abbildung 4: Blockschaltbild und äußere Beschaltung des HX711 Chips[3]
Mit dem Verstärker lassen sich Verstärkungen von 128 (für Eingangsspannungsdifferenzen von ) oder 64 (für Eingangsspannungsdifferenzen von ) einstellen. Für die eben berechneten maximalen Ausgangsspannungsdifferenzen unserer Wägezelle () wird eine Verstärkung von 128 gewählt, sodass bei maximaler Belastung eine verstärkte Spannung von max. erzielt wird. Diese Spannung wird vom 24-Bit A/D-Wandler digitalisiert. Als Referenzspannung für den A/D-Wandler dient die Versorgungsspannung, wodurch sich für eine Quantisierungsstufe eine Auflösung von
ergibt. Bezogen auf unseren Messbereich können also
Werte unterschieden werden. Das bedeutet, dass die theoretisch kleinste messbare Gewichtsänderung
beträgt, was aufgrund von Messrauschen, Vibration (z.B. in Folge der Schrittmotorbewegung), Temperatur- oder sonstigen Umwelteinflüssen in der Praxis nicht erreicht werden kann.
Die Empfindlichkeit des Sensors beschreibt das Verhältnis von Ausgangssignal zu Eingangssignal. Bei diesem Aufbau ist das Ausgangssignal die verstärkte Spannung von und das Eingangssignal das Gewicht von , was zu einer Empfindlichkeit von:
führt. Da der Zusammenhang zwischen der Ausgangsspannung der Brückenschaltung und des Gewichts linear ist, gilt diese Empfindlichkeit für den gesamten Messbereich.
Serielle Schnittstelle
Die dem A/D-Wandler nachgeschaltete Digitalschnittstelle übernimmt die Kommunikation nach außen zu unserem Mikrocontroller. Wenn am Daten-Pin „DOUT“ ein HIGH-Pegel anliegt, so ist die A/D-Wandlung noch nicht abgeschlossen. In dieser Zeit muss der Clock-Pin „PD_SCK“ auf LOW gesetzt sein. Wenn DOUT seinen Pegel von HIGH auf LOW wechselt, ist eine A/D-Wandlung abgeschlossen und es kann der Messwert ausgelesen werden. Dazu müssen 25 Pulse vom Arduino an PD_SCK geschickt werden. Ein Puls ist dabei ein HIGH-Pegel, gefolgt von einem LOW-Pegel, welche beide ca. 1µs gehalten werden sollen. Mit jedem Puls wird ein Bit an den Daten-Pin DOUT weiter geshiftet, welches vom Arduino eingelesen wird. Nach dem 25. Puls wird DOUT wieder auf HIGH gezogen, bis die nächste Wandlung abgeschlossen ist. Das 24-Bit Datum wird als Zweierkomplementzahl, angefangen beim höchstwertigsten Bit, übertragen. Softwareseitig muss der Wert also in einem 32-Bit Integer gespeichert werden. Die Timing-Tabelle zeigt Abbildung 5.
-
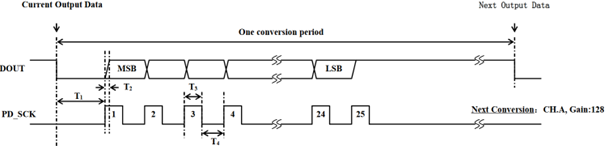
Abbildung 5: Timing-Tabelle der seriellen Datenübertragung [3]
Der Sensor liefert also einen 24-Bit Wert. Da es sich wie beschrieben um lineare Zusammenhänge handelt, kann eine Sensorkalibrierung mit zwei Messpunkten erfolgen. Die erste Messung stellt das „Nullen“ der Rohwerte (Offsetkompensation) dar, sodass sich eine Ursprungsgerade ergibt. Alle Rohdatenmessungen müssen nachfolgend offsetkompensiert genutzt werden. Mit der zweiten Messung lässt sich die Steigung der Geraden berechnen. Eingangswerte sind die offsetkompensierten Rohdaten (x-Achse), Funktionswerte sind die Gewichte in Gramm (y-Achse). Gegeben sind also die Punkte
und
: Offsetkompensierter Rohwert bei Auflegen eines bekannten Kalibriergewichts
: Aufgelegtes, bekanntes Kalibriergewicht in Gramm
Die Steigung (hier mit gekennzeichnet) berechnet sich dann zu
,
sodass die Geradengleichung folgendermaßen aussieht:
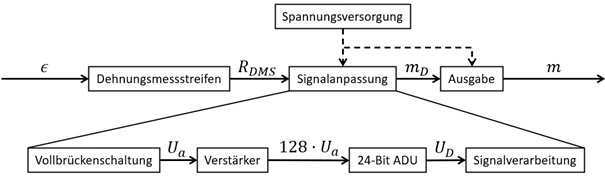
Messkette
Auf Basis der erläuterten Zusammenhänge ergibt sich die Messkette in Abbildung 6.
Die Dehnung wird von den Dehnungsmessstreifen in Widerstände proportional übersetzt. Als Messschaltung liegt die Vollbrückenschaltung vor, dessen Ausgangsspannung von der Verstärkereinheit mit dem Faktor 128 verstärkt wird. Diese Spannung wird dann analog-digital-gewandelt. Die analoge Spannung liegt also jetzt in digitaler Form als 32-Bit Ganzzahl im Speicher des Mikrocontrollers vor. Die Signalverarbeitung zieht von dem Wert den Kalibrieroffset ab und multipliziert ihn mit der Steigung . Das Ergebnis, welches zunächst digital vorliegt, ist die Masse des vermessenden Objekts, also das Gewicht. Zum Schluss erfolgt die Ausgabe des Ergebnisses z.B. auf dem verwendeten Touchdisplay.
Kamoer Peristaltikpumpe
Diese Peristaltikpumpe nutzt einen Schrittmotor als Aktuator, welcher mit dem Arduino über einen A4988-Treiberchip angesteuert werden kann. Vom Arduino lassen sich über Digitalpins die Drehrichtung sowie die Geschwindigkeit in gewissen Grenzen einstellen. Außerdem kann die Motorbewegung über einen Enable-Pin ganz abgeschaltet bzw. eingeschaltet werden. Der Schrittmotor wird um einen Schritt weiterbewegt, wenn der Arduino einen Puls auf den Step-Pin des Treiberchips liefert. Über die Pulsfrequenz kann also die Geschwindigkeit der Drehung des Motors eingestellt werden. Die Pumpe besitzt eine maximale Fördergeschwindigkeit von und wird mit einer Spannung von versorgt. Die zugehörige Softwarekomponente bzw. der Simulink-Block hat folgende Spezifikationen:
Eingänge
- Geschwindigkeit [Steps/s]
| ID | Kapitel | Inhalt | Ersteller | Datum |
| 1 | 1 | Zum Betrieb des Schrittmotors wird die AccelStepper Bibliothek verwendet. Damit lässt sich die vom Regler berechnete Sollgeschwindigkeit direkt einstellen. | Gosedopp | 12.01.2023 |
| 2 | 1 | Sobald die Regeldifferenz hinreichend gering ist, wird keine Motorbewegung mehr zugelassen, d.h. die Geschwindigkeit wird auf 0 gesetzt. | Kachout, Gosedopp | 13.11.2023 |
| 3 | 1 | Am Dir-Pin (Richtungspin) liegt immer der Pegel für die korrekte Pumprichtung an. Da nur in eine Richtung gepumpt wird, ist dieser Pegel konstant und hängt von der Einbaurichtung des Motors ab. | Kachout, Gosedopp | 13.11.2023 |
Touchdisplay
Ein Touchdisplay dient der einfachen Sollwertvorgabe. Hier kann der Benutzer nicht nur das gewünschte Gewicht, sondern auch die Dichte und das Volumen der Flüssigkeit einstellen vorgeben. Um eine einfache Interaktion zu ermöglichen, bietet diese interaktive Mensch-Maschine-Schnittstelle (Human-Machine-Interface, kurz: HMI) eine angemessene Displaygröße, eine ansprechende Oberfläche und die Kompatibilität mit dem Arduino. Die Softwarekomponente ist wie folgt spezifiziert:
Eingänge
- Clock (erzeugt in jedem Sample eine Flanke, ohne funktioniert Simulinkmodell nicht)
Ausgänge
- Sollgewicht [g]
- Istgewicht [g]
| ID | Kapitel | Inhalt | Ersteller | Datum |
| 1 | 2 | Das Sollgewicht (Sollwert der Regelung) wird über das Touchdisplay entweder direkt eingegeben oder über die Formel Sollgewicht = Dichte * Volumen berechnet. | Kachout | 10.11.2023 |
| 2 | 2 | Es gibt einen "Löschen" Button, um falsche Eingaben zu korrigieren. | Kachout | 10.11.2023 |
| 3 | 2 | Im Kalibriermodus wird mit einem bekannten Gewicht kalibriert. | Gosedopp | 10.11.2023 |
| 4 | 2 | Mit den Kalibrierwerten berechnet sich das gemessene Gewicht wie in Abschnitt 4.2 beschrieben über eine lineare Gleichung. | Gosedopp | 10.11.2023 |
| 5 | 2 | Es wird bei Eingaben auf dem Touchdisplay jeweils vorher angezeigt, in welchen Einheiten die Eingaben zu tätigen sind. | Gosedopp | 10.11.2023 |
| 6 | 2 | Das Gewicht wird in , die Dichte in und das Volumen in eingegeben. | Gosedopp | 10.11.2023 |
| 7 | 2 | Läuft die Messung, dann wird das Sollgewicht sowie das Istgewicht auf dem Display angezeigt. | Gosedopp | 10.11.2023 |
| 8 | 2 | Eine laufende Messung kann abgebrochen werden ("Abbruch"-Button). | Gosedopp | 10.11.2023 |
| 9 | 2 | Ist die Messung abgeschlossen, kann durch einen "Fertig"-Button auf die Startseite zurückgekehrt werden. | Gosedopp | 10.11.2023 |
Regler
Eingänge
- Regeldifferenz (Sollgewicht - Istgewicht) [g]
Ausgänge
- Geschwindigkeit [Steps/s]
Parameter
- Kp
| ID | Kapitel | Inhalt | Ersteller | Datum |
| 1 | 3 | Ein stetiger Regler berechnet aus der Regeldifferenz eine Stellgröße. Diese ist konkret die Geschwindigkeit des Motors. | Kachout, Gosedopp | 13.11.2023 |
| 2 | 3 | Negative Regeldifferenzen werden durch einen "Saturation"-Block eliminiert (zu Null gesetzt), da die Pumpe die Flüssigkeit nicht zurückpumpt. | Kachout, Gosedopp | 13.11.2023 |
| 3 | 3 | Die Regelgröße darf nicht überschwingen, ebenfalls aus dem Grund, dass die Pumpe nicht zurückpumpt. | Kachout, Gosedopp | 13.11.2023 |
| 3 | 3 | Der Regler besitzt gutes Führungsübertragungsverhalten, da keine Störungen in Form von Abflüssen vorliegen. | Kachout, Gosedopp | 13.11.2023 |
| 4 | 3 | Der Regler muss in der Lage sein, die Sollgröße stationär zu erreichen. | Kachout, Gosedopp | 13.11.2023 |
Umsetzung (HW/SW)
Hardware
Die Umsetzung der Hardware umfasst die Verkabelung und Verlötung der elektrischen Komponenten, sowie die Entwicklung eines Gehäuses, worin die Komponenten untergebracht werden können.
Für das Gehäuse wird zunächst mittels CAD-Software ein 3D-Modell entworfen, worin auch die einzelnen Komponenten mit deren Abmessungen berücksichtigt werden. Dadurch kann die Anordnung der Komponenten und entsprechende Größen einzelner Bauteile bestimmt werden. Durch den benötigten Bauraum stellt sich heraus, dass ein Gehäuse aus Holz sehr gut umsetzbar ist. In diesem befinden sich dann die Peristaltikpumpe, der ArduinoMega, ein Netzteil zur Spannungsversorgung, ein Spannungswandler, ein Treibermodul für die Pumpe und ein 24bit-Analog-Digital-Umwandler, welcher das Messsignal der Wägezelle verarbeitet. Die Wägezelle selbst wird vor dem Gehäuse montiert. Diese benötigt Abstand zum festen Untergrund und zu dem "Wiegeteller", auf dem das Gefäß, in dem die Flüssigkeit gewogen wird, abgestellt wird. Durch diese Montageweise ist gewährleistet, dass sich die Wägezelle durch die erzeugte Gewichtskraft verformen kann und die Dehnungsmessstreifen eine elektrische Spannung erzeugen. Das HMI zur Eingabe der Flüssigkeitsdosierung wird auf dem Gehäuse montiert, um es einfach bedienen zu können.
Neben dem Gehäuse aus Holz werden weitere Bauteile aus Kunststoff mittels dem Fused Deposition Modelling (FDM) Verfahren gefertigt, welche hauptsächlich die Funktion haben, einzelne Komponenten in Position zu halten.
Folgende Bauteile werden per FDM gefertigt und verbaut:
- Aufnahme für das HMI
- 2 Ausgüsse mit Schlauchdurchführung, inkl. 2 Halter für die Ausgüsse
- Halterung für das Netzteil
- Halterung für die Peristaltikpumpe
- Wiegeteller
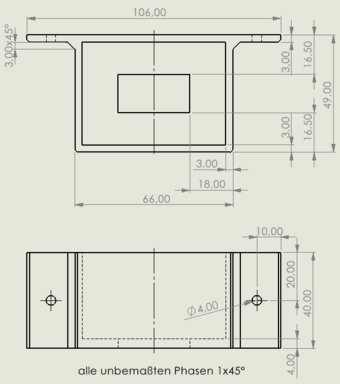
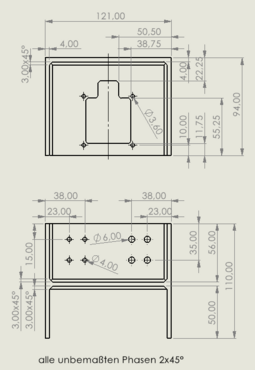
Für die Aufnahme, die Halterung für das Netzteil und die Pumpenhalterung werden zusätzlich zu den reinen 3D-Dateien Zeichnungen angefertigt. Diese sind hier zu sehen:
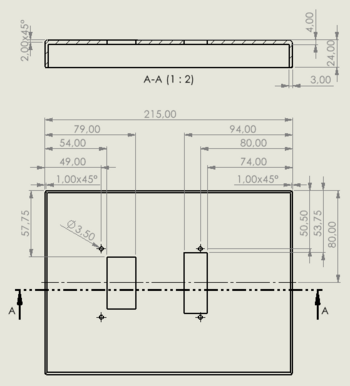 |
 |
 |
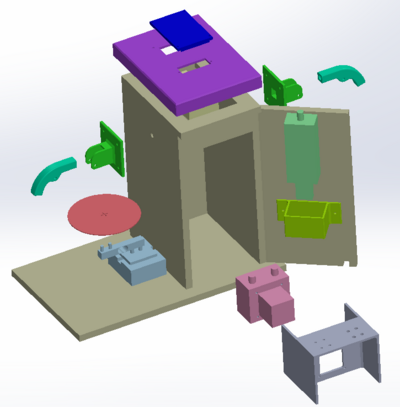
In den folgenden Abbildungen ist das 3D-Modell und darunter die Umsetzung dessen in die Realität zu sehen:
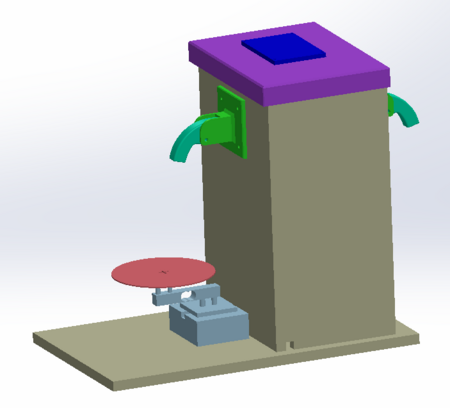 |
 |

Weitere Konstruktionsdateien sind jederzeit zugänglich im SVN der HSHL hinterlegt.
Der Deckel des Gehäuses, lässt sich ein Stück abheben, wodurch ein direkter Zugang zu den Anschlüssen des Arduinos möglich ist. Außerdem lässt sich nun die eingebaute Tür des Gehäuses öffnen. So kann einfach an die innenliegenden Bauteile gelangt werden.
Die verwendeten Schläuche sind nur durch die gedruckten Ausgüsse gesteckt, was ein praktisches Entfernen der Schläuche zwecks Austausch oder Reinigung ermöglicht. Ebenso lässt sich die Pumpe mit samt ihrer Aufnahme aus dem Gehäuse herausziehen, wobei auf die Verkabelung zu achten ist.
Die elektrische Verbindung von HMI zu dem ArduinoMega erfolgt über ein Flachbandkabel. Der Arduino selbst ist so im Gehäuse montiert, dass seine USB-Schnittstelle für eventuelle Änderungen gut zugänglich ist. Alle Verkabelungen, welche vom Arduino abgehen, sowie die Verbindungen am Spannungswandler sind fest verlötet. Die restlichen Verbindungen sind steckbar. Der vordere Ausguss musste nachträglich etwas angehoben werden, um genug Platz für das Einfüllgefäß zu erzeugen.
In folgender Abbildung ist der Verdrahtungsplan zu sehen:
Software
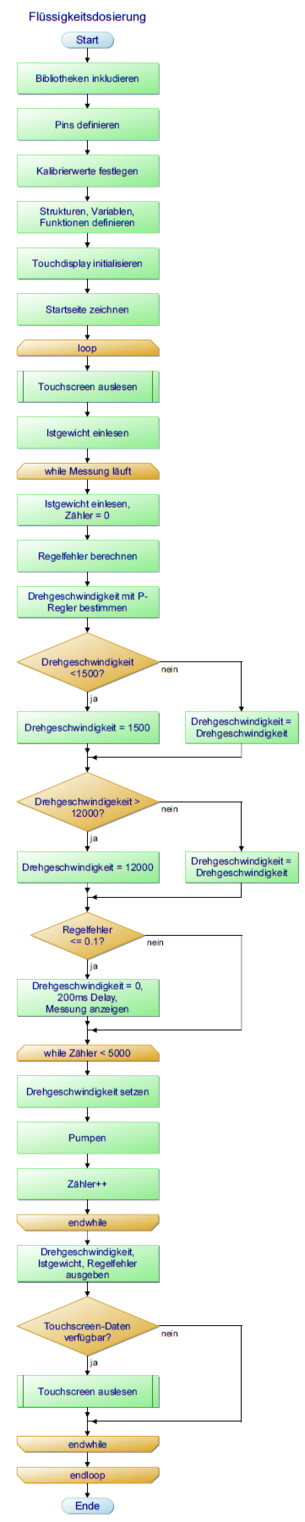
Die Umsetzung der Software für den Mikrocontroller erfolgt in MATLAB/Simulink. Sie besteht aus den wesentlichen Bestandteilen
- Touchdisplay
- Sensorsignalverarbeitung
- Regler
- Pumpenansteuerung
Um die Programmierung übersichtlich zu gestalten wird ein Programmablaufplan erstellt, welcher rechts im Bild zu sehen ist. Bei der Programmierung der Komponenten werden viele Unterfunktionen genutzt, welche zu Zwecken der Übersichtlichkeit nicht alle einzeln im Ablaufplan aufgeführt sind. So sind vor allem Touchdisplay und Sensorsignalverarbeitung eng miteinander verknüpft und werden daher innerhalb eines Blocks umgesetzt. Für das Touchdisplay werden mehrere externe Bibliotheken genutzt, mit denen der Touchpunkt ausgelesen und die Anzeige von Text bzw. die Erstellung von Buttons ermöglicht wird. Für die Sensorsignalverarbeitung sind Bitshift-Operationen notwendig. Beides führt dazu, dass nicht mehr nur mit Standard-Simulink-Blöcken gearbeitet werden kann, sondern der C++ Code direkt in einem S-Function-Builder Block untergebracht werden muss. Welche Einstellungen man in dem Block tätigen muss, zeigt der Artikel Erstellen eigener S-Functions.
Touchdisplay
Die Software des Touchdisplays erfordert die Bibliotheken UTFT, UTFT_Buttons und URTouch, welche in der S-Function hinzugefügt werden müssen. Anschließend kann jede Seite nach vorab überlegtem Konzept implementiert werden. Da der Code dazu sehr lang ist, sei an dieser Stelle auf die Dokumentation der Bibliotheken unter den jeweiligen Links sowie unserer kommentierten Implementierung in SVN verwiesen. Wie eine einzelne Seite dargestellt wird, zeigt nichtsdestotrotz folgender Code-Schnipsel:
/***********************************************
Funktion zum Zeichnen der Startseite auf dem LCD
***********************************************/
// Parameter: Zeiger auf UTFT_Buttons Objekt
void drawStartseite(UTFT_Buttons *myButtons)
{
// Display bereinigen
myGLCD.clrScr();
// Alle alten Buttons löschen
myButtons->deleteAllButtons();
// Neue Buttons anlegen. In diesem Fall zwei Buttons
but1 = myButtons->addButton( 10, 140, 300, 30, "Messen");
but2 = myButtons->addButton( 10, 180, 300, 30, "Kalibrieren");
// Buttons zeichnen
myButtons->drawButton(but1);
myButtons->drawButton(but2);
// Hintergrundfarbe und Textfarbe einstellen (RGB)
myGLCD.setBackColor(0, 0, 0); // Hintergrund schwarz
myGLCD.setColor(255, 255, 255); // Text weiß
// Text zeilenweise auf Display anzeigen
myGLCD.print("Gewichtsgeregelte", CENTER, 50);
myGLCD.print("Fluessigkeits-", CENTER, 70);
myGLCD.print("dosierung", CENTER, 90);
// Interne Variable für die aktuelle Seite zum späteren Abfragen
seite = 1;
}
Die Abfrage eines Buttons sähe dann so aus:
// Wird das Display gedrückt?
if (myTouch.dataAvailable() == true)
{
// Wenn die aktuelle Seite die Startseite ist, dann...
if (seite == 1)
{
// ...überprüfe, welcher Button gedrückt wurde
but = myButtons.checkButtons();
// Wenn das der erste Button, also "Messen" war, dann...
if (but == but1)
{
// ...zeichne die zugehörige nächste Seite "Messen"
drawMessen(&myButtons);
}
// Wenn das der zweite Button, also "Kalibrieren" war, dann...
else if (but == but2)
{
// ...zeichne die zugehörige nächste Seite "Kalibrieren1"
drawKalibrieren1(&myButtons);
}
// Ansonsten nichts machen
}
}
Sensorsignalverarbeitung
Wie bereits ausführlich erläutert, liefert der Sensor seriell eine 24-Bit Zweierkomplementzahl, welche entsprechend der Timing-Chart eingelesen werden muss. Der Code dazu sieht so aus:
/************************************************
Funktion zum Empfangen des übertragenen Rohwerts
************************************************/
float scaleGetRaw()
{
// Solange der Datenpin auf HIGH ist, ist die Messung noch nicht abgeschlossen
while (digitalRead(myScale.dataPin) == HIGH)
{
// Scheduler freigeben
yield();
}
// Union zum Byteweisen Datenempfang
union
{
// Variable vom Datentyp 32-Bit Zweierkomplementzahl
long value;
// Array vom Datentyp vorzeichenlose 8-Bit Ganzzahl
uint8_t data[4];
} rohwert; // Direktes Anlegen Variable des Union Datentyps
// Wert Nullen
rohwert.value = 0;
// Interrupts blockieren, ansonsten Übertragungsfehler möglich
noInterrupts();
// 25 Pulse an den Clock-Pin aussenden
// In den ersten 24 Pulsen die geshifteten Daten am Datenpin auslesen
rohwert.data[2] = shiftIn(myScale.dataPin, myScale.clockPin, MSBFIRST);
rohwert.data[1] = shiftIn(myScale.dataPin, myScale.clockPin, MSBFIRST);
rohwert.data[0] = shiftIn(myScale.dataPin, myScale.clockPin, MSBFIRST);
// 25. Puls, um die Verstärkung auf 128 zu halten
digitalWrite(myScale.clockPin, HIGH);
digitalWrite(myScale.clockPin, LOW);
// Interrupts wieder erlauben
interrupts();
// Vorzeichen von 24-Bit Wert an 32-Bit Wert anpassen
if (rohwert.data[2] & 0x80)
{
rohwert.data[3] = 0xFF;
}
// Rohwert als Fließkommazahl zurückgeben
return 1.0 * rohwert.value;
}
Daraus wird das Istgewicht mit der ebenfalls bereits erklärten linearen Gleichung berechnet:
/***********************************************
Funktion zum berechnen des Messwerts in Gramm
***********************************************/
float scaleRead()
{
// Wert einlesen und lineare Gleichung anwenden
float units = myScale.scale * (scaleGetRaw() - myScale.offset);
// Wert zurückgeben
return units;
}
Regler
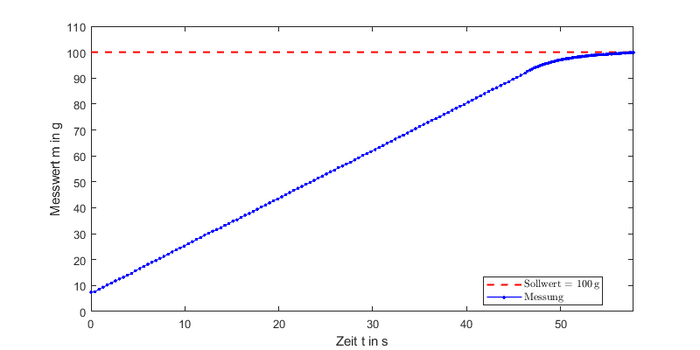
Zur Implementierung und Auslegung des Reglers wird zunächst ein Modell der Regelstrecke, also des Systems erstellt. Dieses Modell wird experimentell ermittelt, indem ein Sollwertsprung der Motorgeschwindigkeit in eingeleitet wird:
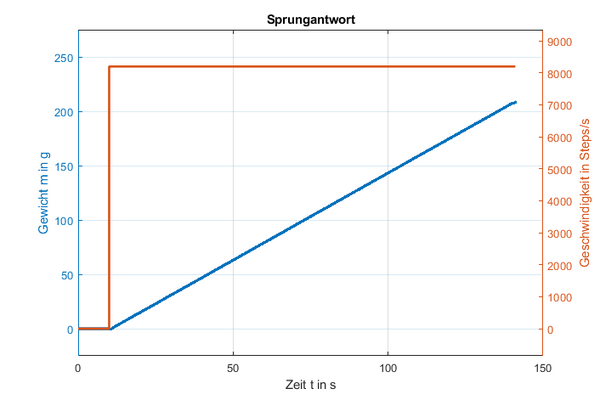
Nach ca. 145 Sekunden wurde das Experiment abgebrochen, da das I-Verhalten dieses Systems eindeutig ist.
Aus der ermittelten Regelstrecke und den weiteren Komponenten dieses Projektes ergibt sich folgender Regelkreis:
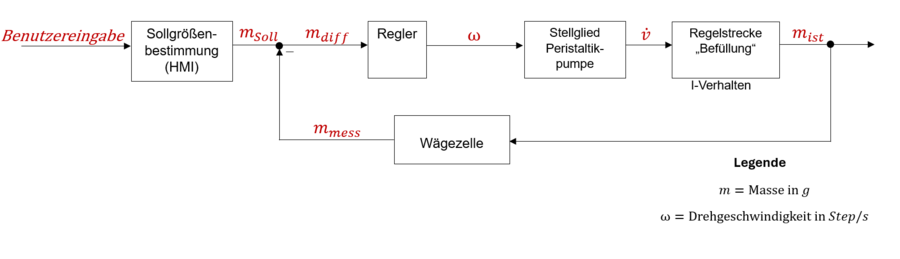
Um die richtige Reglerart zu bestimmen, welche nötig ist, um eine bleibende Regelabweichung zu verhindern und dennoch den statischen Endwert erreicht, wird die Führungsübertragungsfunktion des geschlossenen Regelkreises für einen P-Regler betrachtet:
Fehler beim Parsen (Syntaxfehler): {\displaystyle G_W=\frac{G_R\cdot G_S}{1+G_R\cdot G_S\cdot G_M}}
Mit Fehler beim Parsen (Syntaxfehler): {\displaystyle G_S=\frac{k_I}{s}}
und Fehler beim Parsen (Syntaxfehler): {\displaystyle G_P=k_P}
und Fehler beim Parsen (Syntaxfehler): {\displaystyle G_M=1}
(ideal)
ergibt sich folgende Gesamtübertragungsfunktion:
Fehler beim Parsen (Syntaxfehler): {\displaystyle G_{WP}=\frac{k_P\cdot k_I}{s+k_P\cdot k_I}}
Diese Übertragungsfunktion erreicht den statischen Endwert:
Fehler beim Parsen (Syntaxfehler): {\displaystyle x_{stat}=\lim_{{s \to 0}}G_{WP}=\frac{k_P\cdot k_I}{0+k_P\cdot k_I}=1 }
Hiermit ist bewiesen, dass ein einfacher P-Regler für unsere Zwecke ausreichend ist.
Reglerauslegung
Zur Auslegung des Reglers wird zunächst ein separates Simulink-Modell zur reinen Simulation des Regelkreises erstellt.
Hier wird durch verschiedene Einstellungen des Verstärkungsfaktors das gewünschte Regelverhalten angenähert. Dabei wird beachtet, dass der Regler nicht zu früh die Geschwindigkeit reduziert, da dies den Befüllungsprozess unnötig in die Länge ziehen würde. Andererseits darf die Geschwindigkeit auch nicht zu spät reduziert werden. Dies hätte ein ungenaueres Dosieren zur Folge. Folgend sind die Simulationsergebnisse für verschiedene dargestellt:
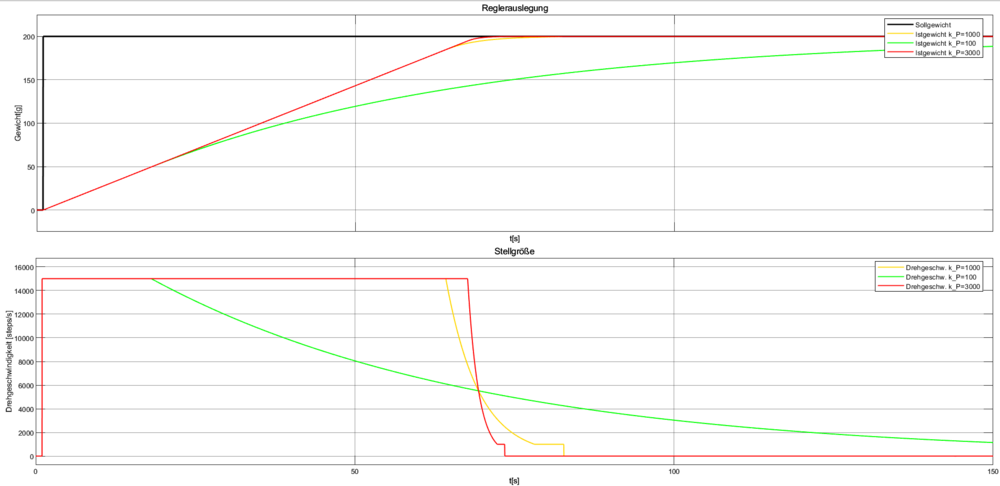
Hieraus lässt sich schon erkennen, dass Fehler beim Parsen (Syntaxfehler): {\displaystyle k_P=100 \frac{\text{Steps}}{\text{s}\cdot \text{g}}}
für das reale System nicht sinnvoll wäre, da der Regler sehr früh beginnt die Drehzahl zu verringern und das Befüllen sehr lange dauert.
Nach erster Annäherung wird das Führungsübertragungsverhalten am realen System getestet und feinjustiert. So wird nach einigen Messungen ein Verstärkungsfaktor von:
Fehler beim Parsen (Syntaxfehler): {\displaystyle k_P=1500 \frac{\text{Steps}}{\text{s}\cdot \text{g}}}
festgelegt. Dieser erweist sich als hoch genug, um nicht zu viel Zeit zu verlieren und regelt trotzdem sehr genau.
Der P-Regler genügt also den Anforderungen und wird vollständig in Simulink umgesetzt. Das Subsystem für die Reglerimplementierung sieht in Simulink folgendermaßen aus:
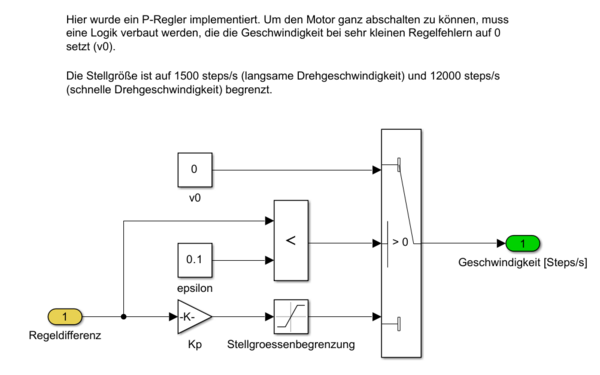
Pumpenansteuerung
Für diese Softwarekomponente wird ebenfalls eine S-Function erstellt, um die AccelStepper Bibliothek nutzen zu können. Mit dieser lassen sich dann einfach verschiedene Befehle ausführen, um zum Beispiel ein Geschwindigkeitslimit zu setzen, die aus dem P-Regler bestimmte Geschwindigkeit zuzuweisen und den Stepmotor laufen zu lassen.
Komponententest
Touchdisplay
Der Touchdisplay-Block in Simulink besitzt keine Eingänge. Die Eingänge könnte man in diesem Fall als die Benutzereingaben verstehen, weshalb jeder Button in den Tests einmal gedrückt und das Verhalten untersucht wurde. Um die Testfälle etwas übersichtlicher zu gestalten, wird nicht jeder Button aufgeführt. Die Buttons sind auf den verschiedenen Seiten immer gleich positioniert und softwareseitig charakterisiert. Pro Seite sind max. zwei Aktionsbuttons, die einen Seitenwechsel auslösen, implementiert worden. Außerdem gibt es auf einigen Seiten einen "Zurück"-Button, welche ebenfalls separat gestestet wird.
Eingänge
Benutzereingabe
Ausgänge
Sollgewicht [g]
| Testfall-ID | Testfall-Name | Anforderung | Vorbedingungen und Eingänge | Aktionen | Erwartetes Ergebnis | Ergebnis | Bewertung | Kommentar |
| 01 | Button "Messen" auf Startseite | 004 | Startseite geladen | Button "Messen" wird gedrückt | Messseite wird geöffnet | Messseite wird geöffnet | Erfolgreich | Dieser Test steht stellvertretend für den jeweils oberen Aktionsbutton einer Seite. |
| 02 | Button "Kalibrieren" auf Startseite | 004 | Startseite geladen | Button "Kalibrieren" wird gedrückt | Kalibrierseite wird geöffnet | Kalibrierseite wird geöffnet | Erfolgreich | Dieser Test steht stellvertretend für den jeweils unteren Aktionsbutton einer Seite. |
| 03 | Button "Zurück (<)" | 004 | Messseite geöffnet | Button "Zurück (<)" wird gedrückt | Es wird auf die Startseite zurückgegekehrt | Es wird auf die Startseite zurückgegekehrt | Erfolgreich | Dieser Test steht stellvertretend für alle Zurück-Buttons. |
| 04 | Direkte Gewichtseingabe | 004, 011 | Gewichtsseite geöffnet | Die Buttons für die Ziffern 0-9 werden in beliebiger Reihenfolge gedrückt | Die eingegebenen Ziffern werden auf dem Display in der korrekten Reihenfolge angezeigt | Die eingegebenen Ziffern werden auf dem Display in der korrekten Reihenfolge angezeigt | Erfolgreich | Dieser Test steht stellvertretend für alle Eingabeseiten, da diese immer gleich aufgebaut und implementiert sind. |
| 05 | Gewichtseingabe löschen | 004, 011 | Gewichtsseite geöffnet | Die Buttons für die Ziffern 0-9 werden in beliebiger Reihenfolge gedrückt. Danach wird der Löschen Button gedrückt | Der "Löschen" Button setzt die Eingabe komplett zurück | Der "Löschen" Button setzt die Eingabe komplett zurück | Erfolgreich | Dieser Test steht stellvertretend für alle Eingabeseiten, da diese immer gleich aufgebaut und implementiert sind. |
| 06 | Direkte Gewichtseingabe - Sollwert in Simulink | 004, 011 | Gewichtsseite geöffnet | Über die Buttons wird ein Sollgewicht von 987 Gramm eingegeben | In Simulink werden 987 Gramm angezeigt | In Simulink werden 987 Gramm angezeigt | Erfolgreich | |
| 07 | Direkte Gewichtseingabe - Sollwertbegrenzung | 004, 011 | Gewichtsseite geöffnet | Über die Buttons wird ein Sollgewicht von > 1000 Gramm eingegeben | Hinweis erscheint, dass das Maximalgewicht überschritten wurde. Das Gewicht kann erneut eingegeben werden | Hinweis erscheint, dass das Maximalgewicht überschritten wurde. Das Gewicht kann erneut eingegeben werden | Erfolgreich | |
| 08 | Gewichtseingabe über Dichte und Volumen | 004, 011 | Dichte & Volumen-Seite geöffnet | Über die Buttons wird ein Sollgewicht von > 1000 Gramm eingegeben | Hinweis erscheint, dass das Maximalgewicht überschritten wurde. Das Gewicht kann erneut eingegeben werden | Hinweis erscheint, dass das Maximalgewicht überschritten wurde. Das Gewicht kann erneut eingegeben werden | Erfolgreich | |
| 09 | Gewichtseingabe über Dichte und Volumen - Sollwert in Simulink | 004, 011 | Dichte & Volumen-Seite geöffnet | Über die Buttons wird eine Dichte von 997 kg/m³ und ein Volumen von 1000ml eingegeben | Der Sollwert erscheint in Simulink korrekt berechnet zu 997 Gramm | Der Sollwert erscheint in Simulink korrekt berechnet zu 997 Gramm | Erfolgreich | Formel zur Umrechnung: für und |
| 10 | Gewichtseingabe über Dichte und Volumen - Sollwertbegrenzung | 004, 011 | Dichte & Volumen-Seite geöffnet | Die eingegebene Kombination von Dichte und Volumen ergibt ein Sollgewicht von > 1000 Gramm | Hinweis erscheint, dass das Maximalgewicht überschritten wurde. Dichte & Volumen können erneut eingegeben werden | Hinweis erscheint, dass das Maximalgewicht überschritten wurde. Dichte & Volumen können erneut eingegeben werden | Erfolgreich | |
| 11 | Laufende Messung - Anzeige Sollgewicht | 004, 011 | Messung gestartet, Gewicht < 1000 Gramm | Das Sollgewicht wird auf dem Display korrekt angezeigt | Das Sollgewicht wird auf dem Display korrekt angezeigt | Erfolgreich | ||
| 12 | Laufende Messung - Abbruch | 004, 011 | Messung gestartet, Gewicht < 1000 Gramm | Während der laufenden Messung wird der Abbruch-Button betätigt | Die Pumpe bleibt stehen und es wird auf die Startseite zurückgekehrt | Die Pumpe bleibt stehen und es wird auf die Startseite zurückgekehrt | Erfolgreich | |
| 13 | Abgeschlossene Messung - Anzeige Istgewicht | 004, 011 | Messung abgeschlossen, Gewicht < 1000 Gramm | Das Istgewicht wird nach Abschluss der Messung auf dem Display korrekt angezeigt | Das Istgewicht wird nach Abschluss der Messung auf dem Display korrekt angezeigt | Erfolgreich | Anzeige während der Messung nicht möglich, da der Schrittmotor sonst merklich ruckelt. | |
| 14 | Abgeschlossene Messung - Fertig | 004, 011 | Messung abgeschlossen, Gewicht < 1000 Gramm | Nach abgeschlossener Messung erscheint ein "Fertig" Button, mit dem durch Betätigen auf die Startseite zurückgekehrt wird. Dieser Button wird gedrückt. | Es wird auf die Startseite zurückgekehrt | Es wird auf die Startseite zurückgekehrt | Erfolgreich | |
| 15 | Kalibriermodus | 004, 012 | Der Zielbehälter wird auf den Wiegeteller aufgelegt. Die Kalibrierung wird durch den "Start" Button gestartet. Danach wird eine 526 Gramm schwere Hantelscheibe mit auf den Wiegeteller gelegt und der "Weiter" Button gedrückt. | Die Messung von verschiedenen bekannten Gewichten nach der Kalibrierung ist korrekt | Die Messung von verschiedenen bekannten Gewichten nach der Kalibrierung ist korrekt | Erfolgreich | Hier kann noch eine Verbesserung erzielt werden. Siehe Abschnitt Ausblick. |
Sensorsignalverarbeitung
Die Sensorsignalverarbeitung befindet sich im gleichen S-Function-Block, wie die Touchscreen-Funktionen.
Eingänge
Keine
Ausgänge
Istgewicht [g]
Parameter
Skalierungsfaktor (Steigung der Kalibrier-Geraden)
Offset zum "Nullen" der Wägezelle
| Testfall-ID | Testfall-Name | Anforderung | Vorbedingungen und Eingänge | Aktionen | Erwartetes Ergebnis | Ergebnis | Bewertung | Kommentar |
| 16 | Auslesen des A/D-gewandelten Rohwerts | 005, 013 | Der Rohwert wird seriell gemäß der Timing-Tabelle des HX711-Datenblatts durch 25 Clock-Pulse als Zweierkomplementzahl empfangen | Es wird ein Rohwert empfangen, dessen Wert allerdings erstmal nicht aussagekräftig ist | Der Rohwert wird empfangen | Erfolgreich | Ohne Kalibrierung kann man mit diesen Werten nichts anfangen. Hier sollte lediglich die generelle Funktionsweise der Übertragung getestet werden. | |
| 17 | Umrechnen des Rohwerts in ein Istgewicht | 005, 013 | Kalibrierparameter zuvor berechnet | Der Rohwert wird der bereits beschriebenen Geradengleichung zu einem Istgewicht umgerechnet. Dazu werden verschiedene bekannte Gewichte auf den Wiegeteller gelegt | Die Gewichte werden korrekt berechnet und in Simulink ausgegeben | Die Gewichte werden korrekt berechnet und in Simulink ausgegeben | Erfolgreich |
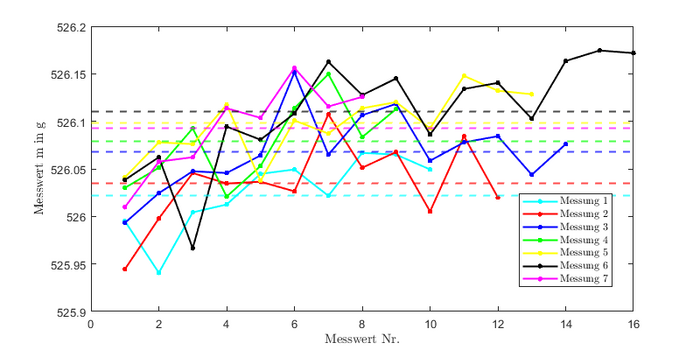
Außerdem wurde die Wiederholgenauigkeit des Sensors anhand statischer Messungen mit dem gleichen Gewicht analysiert. Das Gewicht wurde mehrmals aufgelegt, dann heruntergenommen und erneut aufgelegt, was zu folgendem Ergebnis führte:
Die gestrichelten Linien stellen den Mittelwert der jeweiligen Messung dar. Erkennbar ist, dass die Wiederholgenauigkeit für unseren Anwendungszweck hinreichend gut ist. Die maximale Differenz im Mittelwert zwischen zwei Messungen beträgt nur .
Die Stabilität des Sensors wird über eine längere statische Messung bewertet. Dazu werden bekannte Gewichte auf dem Wiegeteller platziert und Mittelwert, Standardabweichung und der generelle Verlauf der Messgröße betrachtet.
Es ist zu erkennen, dass der Mittelwert nicht ganz bei Null liegt, jedoch mit nicht sehr weit davon entfernt. Die Standardabweichung ist mit ebenfalls sehr klein, der Sensor erscheint also stabil. Dies bestätigen auch die Messungen mit zwei weiteren Gewichten:
Da das genaue Gewicht in beiden Fällen nicht auf Nachkommastellen bekannt ist, kann hier keine Aussage bezüglich der Abweichung des Mittelwerts von dem tatsächlichen Wert getroffen werden. Jedoch ist klar erkennbar, dass die Standardabweichungen in beiden Fällen ähnlich gering sind, wie bei der Messung ohne Auflagegewicht. Bei der Messung in Abbildung 22 ist am Ende ein leichter Trend "nach oben" zu erkennen, der sich allerdings im Milligrammbereich befindet. Alles in allem lässt sich festhalten, dass die Stabilität des Sensors hervorragend ist.
Für die Messunsicherheit nach GUM (Guide to the Expression of Uncertainty in Measurement)[4] werden für die Wägezelle die statische Messung mit sowie die Angaben in dessen Datenblatt genutzt werden. Für die Messunsicherheit Typ A ergeben sich die in der Legende der Abbildung 21 angegebenen Werte für den empirischen Mittelwert und die empirische Standardabweichung. Die Standardunsicherheit nach Typ A berechnet sich dann zu:
mit
: Vertrauensfaktor der Student-t-Verteilung
: Anzahl Messungen
: Empirische Standardabweichung
Der Vertrauensfaktor der Student-t-Verteilung wurde mit der MATLAB Statistics Toolbox berechnet. Es ergibt sich:
Im Datenblatt[5] finden sich folgende Angaben, die zur Messunsicherheit Typ B führen:
- Nichtlinearität: des Messbereichs
- Verzögerung: des Messbereichs
- Wiederholgenauigkeit: des Messbereichs
Was zur Messunsicherheit Typ B führt:
mit
: Anteil der Messunsicherheit durch Nichtlinearität
: Anteil der Messunsicherheit durch Verzögerung
: Anteil der Messunsicherheit durch Wiederholgenauigkeit
Für den Messbereich von und mit Dezimalwerten, statt Prozentwerten, ergibt sich:
Für die Unsicherheiten der drei Einflussgrößen wird jeweils eine Gleichverteilung angenommen, weshalb die Anteile jeweils noch durch geteilt werden. Die Messunsicherheit Typ C berechnet sich aus der Wurzel der Summe der Quadrate aus Typ A und Typ B:
,
welche noch mit dem Vertrauensfaktor für das Vertrauensniveau von zur erweiterten Messunsicherheit verrechnet werden kann:
Dieses Ergebnis lässt sich so interpretieren, dass bei aller Messungen der Messwert garantiert nicht weiter als abweicht. Dies erfüllt unsere Anforderungen an die Genauigkeit exakt.
Regler
Eingänge
Regeldifferenz
Ausgänge
Geschwindigkeit
Parameter
Proportionalverstärkung
| Testfall-ID | Testfall-Name | Anforderung | Vorbedingungen und Eingänge | Aktionen | Erwartetes Ergebnis | Ergebnis | Bewertung | Kommentar |
| 18 | Regelbetrieb | 005, 013, 014 | Regeldifferenz = | Simulink-Testumgebung starten durch Klick auf "Run" | Die Stellgröße beträgt | Stellgröße | Erfolgreich | |
| 19 | Stellgrößenbegrenzung 1 | 005, 013, 014 | Regeldifferenz = , sodass Stellgröße wird | Simulink-Testumgebung starten durch Klick auf "Run" | Die Stellgröße wird auf die Maximalgeschwindigkeit von begrenzt | Stellgröße | Erfolgreich | |
| 20 | Stellgrößenbegrenzung 2 | 005, 013, 014 | Regeldifferenz = , sodass Stellgröße wird | Simulink-Testumgebung starten durch Klick auf "Run" | Die Stellgröße wird auf die Minimalgeschwindigkeit von begrenzt | Stellgröße | Erfolgreich | Ein Unterschreiten dieser Geschwindigkeit kann ggf. zum Stillstand des Motors führen, obwohl das Zielgewicht noch nicht erreicht wurde. |
Pumpenansteuerung
Eingänge
Geschwindigkeit in
| Testfall-ID | Testfall-Name | Anforderung | Vorbedingungen und Eingänge | Aktionen | Erwartetes Ergebnis | Ergebnis | Bewertung | Kommentar |
| 21 | Sollgeschwindigkeit setzen | 003, 013 | Geschwindigkeit setzen | Pumpe läuft | Pumpe läuft | Erfolgreich | ||
| 22 | Min. Sollgeschwindigkeit testen | 003, 013 | Geschwindigkeit setzen | Pumpe pumpt nur minimal Flüssigkeit | minimale Sollgeschwindigkeit von | Erfolgreich | ||
| 23 | Max. Sollgeschwindigkeit testen | 003, 013 | Geschwindigkeit setzen | Pumpe pumpt möglichst schnell | maximale Sollgeschwindigkeit von | Erfolgreich | ||
| 24 | Sollgeschwindigkeit mittels Regler | 003, 013 | Regler und Messung funktionieren | Geschwindigkeit durch Regler setzen | Pumpe pumpt mit vorgegebener Geschwindigkeit, anfangs schnell, gegen stat. Endwert hin langsamer | Pumpe pumpt mit vorgegebener Geschwindigkeit, anfangs schnell, gegen stat. Endwert hin langsamer | Erfolgreich | Dieser Test wurde erst nach Zusammenbau getestet, da mehrere Komponenten mit einwirken. |
| 25 | Stopp bei geringer Regeldifferenz | 003, 013 | Regler und Messung funktionieren | Grenze Regeldifferenz setzen | Motorstop bei erreichter Grenze | Motor stoppt | Erfolgreich | Der Regler stoppt die Pumpe automatisch. Die eingestellte Grenze wird lediglich zur Begrenzung der minimalen Sollgeschwindigkeit genutzt. |
| 26 | Pumpenrichtung | 003, 013 | Flüssigkeitsbehälter inkl. Verschlauchung vorhanden | Dir-Pin = "Low" | Flüssigkeit wird in das Gefäß auf der Wägezelle gepumpt. | Flüssigkeit wird in das Gefäß auf der Wägezelle gepumpt. | Erfolgreich |
Ergebnis
Nach Durchführung der Komponententests konnte das Gesamtsystem in Betrieb genommen werden. Zum Test wurden für die Flüssigkeiten Wasser, Milch und Speiseöl verschiedene Sollwerte auspropbiert, dessen Ergebnisse im Folgenden einmal dargestellt werden.
Dosierung von Wasser
Für Wasser wurden drei Test durchgeführt. Beim ersten Test wurde ein Sollwert von vorgegeben.
Hier ist gut das I-Verhalten der Regelstrecke ersichtlich. Außerdem kann man die Arbeitsweise des P-Reglers erkennen, der ab einer bestimmten Schwelle beginnt, die Geschwindigkeit des Motors zu verringern, um sich dem Zielwert langsam und präzise anzunähern. Der erreichte Endwert liegt bei , was einer Abweichung von entspricht. Im nächsten Test wird der Sollwert mit vorgegeben.
Bei dieser Messung ergibt sich ein ähnlicher Verlauf. Der Endwert beträgt , was einer Abweichung von entspricht. Der letzte Test soll das Maximum des regelbaren Gewichts von ausprobieren.
Hier beträgt der Endwert , die Abweichung beträgt .
Dosierung von Milch
Aufgrund der erfolgreichen Tests mit Wasser, wird für Milch und Speiseöl nur jeweils ein Test durchgeführt.
Es ergibt sich ein Endwert von , die Abweichung beträgt .
Dosierung von Speiseöl
Bei diesem Test betrug der Endwert , also einer Abweichung von
Fazit
Alle Systemtests waren erfolgreich und haben die Genaugikeitsanforderung deutlich übertroffen (annährend um das 8 bis 10-fache). Damit eignet sich dieser Aufbau optimal, um Flüssigkeiten bis zu einem Gewicht von präzise zu dosieren.
Zusammenfassung
Das Ziel dieses Projekts war es, ein System zu entwicklen, mit dem es möglich ist, Flüssigkeiten grammgenau zu dosieren. Anwendung findet ein solcher Aufbau beispielsweise in der Chemieindustrie zum Abfüllen von Reinigungs-/Pflegeprodukten. Uns war außerdem wichtig, dass es sich um ein Tischprojekt handelt, um ortsunabhängigkeit zu gewährleisten. Unser Aufbau besteht aus den Eingabe/Verarbeitung/Ausgabe-Komponenten Wägezelle und Touchdisplay (E)/Arduino MEGA 2560 (V)/Schrittmotor und Touchdisplay (A). Die Wägezelle ermöglicht über eine erläuterte Signalaufbereitungs-/Signalverarbeitungskette die Messung des Gewichts der zugrundeliegenden Flüssigkeit. Auf dem Mikrocontroller des Arduino-Boards wird eine Regeldifferenz berechnet, sodass ein P-Regler dem Schrittmotor eine Geschwindigkeit vorgeben kann. Die Ergebnisse zeigen, dass der Aufbau vollständig funktioniert und die gestellten Anforderungen erfüllt werden.
Lessons Learned
Dieses Projekt hat uns gelehrt, ein System gemäß V-Modell von der Anforderungsdefinition, bis zu den Komponententests und der Inbetriebnahme zu entwickeln. Dabei waren Kenntnisse in der Elektrotechnik, Informatik bzw. Embedded Software Entwicklung sowie dem Projektmanagement erforderlich. Der unterschiedliche Wissenstand der Gruppenmitglieder konnte dadurch zum Teil angeglichen werden. Es wurden aber auch die Stärken der Gruppenmitglieder gezielt ausgenutzt, um schneller ans Ziel zu kommen, da auch in Projekten in Unternehmen mehrere Menschen mit unterschiedlichen Aufgaben in Teams zusammenarbeiten. Des Weiteren sind als Lessons Learned die folgenden Punkte besonders hervorzuheben:
- Viel Arbeitsleistung in der Entwurfsphase macht die Implementierungs-/Umsetzungsphase deutlich einfacher
- Umgang mit einem Lötkolben sowie mit Entlötlitzen und -pumpen
- Pfostenstecker mit Flachbandkabel verknüpfen
- Umgang mit elektronischer Hardware, Zusammenspiel der Komponenten, Spannungsversorgung handhaben
- Erstellung von S-Functions in Simulink
- Konstruktion von 3D-Druck-Teilen in SolidWorks
Ausblick
Im Folgenden soll ein kurzer Ausblick auf künftige Verbesserungen des Systems gegeben werden, die im Laufe der Umsetzung aufgekommen sind.
- Zwar funktioniert das System einwandfrei, jedoch erfolgt das Pumpen der Flüssigkeit nur sehr langsam. Dies ist dem Fakt geschuldet, dass wir im Team noch keinerlei Erfahrung mit Pumpen hatten und schlecht einschätzen konnten, was angemessene Pumpgeschwindigkeiten sind. Außerdem ist die Ansteuerung des Schrittmotors nicht optimal umgesetzt worden. Hier wurde auf eine Bibliothek zurückgegriffen, die, wenn die Pumpe laufen soll, permanent eine Funktion aufrufen muss. Weil die Software aber noch andere Bausteine besitzt, kommt es zu einem deutlich hörbarem Ruckeln oder der Motor läuft erst garnicht an. Daher wurde eine Messung immer nur in einigen Programmzyklen genommen. Hier könnte in Zukunft auf die Bibliothek verzichtet und evtl. mit Hardware-Interrups gearbeitet werden. Der Step-Pin des Motortreibers wird dann vom Timer-Baustein des Mikrocontrollers per Interrupt in der für die Sollgeschwindigkeit entsprechenden Frequenz gepulst. Da die vollumfängliche Implementierung dieser Funktion aber aufwendig ist und dem entwickeln einer eigenen Bibliothek gleichbedeutend ist, wurde sich für den Weg der Nutzung einer Bibliothek entschieden. Eine Alternative wäre es, statt eines Schrittmotors einen Gleichstrommotor zu verwenden, der mittels Pulsweitenmodulation (PWM) angesteuert wird.
- Ein weiteres Verbesserungspotential ergibt sich in der Anwendung des Aufbaus: Wenn z.B. in einem Messvorgang Öl dosiert wurde und im nächsten Vorgang Wasser dosiert werden soll, dann müssen die Schläuche gereinigt werden. Ein Reinigungsmodus war allerdings nicht vorgesehen und ist aktuell auch nicht implementiert. Die Schläuche müssen also ausgebaut und manuell gereinigt werden, was allerdings auch möglich ist.
- Zum Kalibrieren der Waage sollten eigentlich auf mehrere Nachkommastellen genaue Kalibriergewichte genutzt werden. Da diese in der Anschaffung aber sehr teuer sind, haben wir uns dagegen entschieden und eine Präzisionswaage als "Kalibrator" verwendet. Nach [[1], S. 23] sollte zur Messung des Wertes des Kalibriergewichts ein um drei bis sechs Zehnerpotenzen genaueres Messmittel genutzt werden, was bei uns nicht der Fall war. Auf diese Weise könnten die Messergebnisse sicherlich noch deutlich verbessert werden.
- Ebenso lassen sich später die festen Werte des Kalibriergewichtes im EEPROM des Mikrocontrollers speichern, sodass eine durchgeführte Kalibrierung auch nach Unterbrechung der Stromversorgung erhalten bleibt.
- Der Kalibriervorgang kann dahingehend erweitert werden, dass das Kalibriergewicht ebenfalls eingegeben werden kann. Aktuell muss immer das gleiche Kalibriergewicht genutzt werden (Hantelscheibe 526 Gramm), weil dies in der Software so hinterlegt ist.
Projektunterlagen
Die relevanten Projektunterlagen wie das Gesamtmodell, die Testumgebungen etc. finden sich im ZIP-Archiv zum Download: Datei:Fluessigkeitsdosierung.zip.
Projektplan
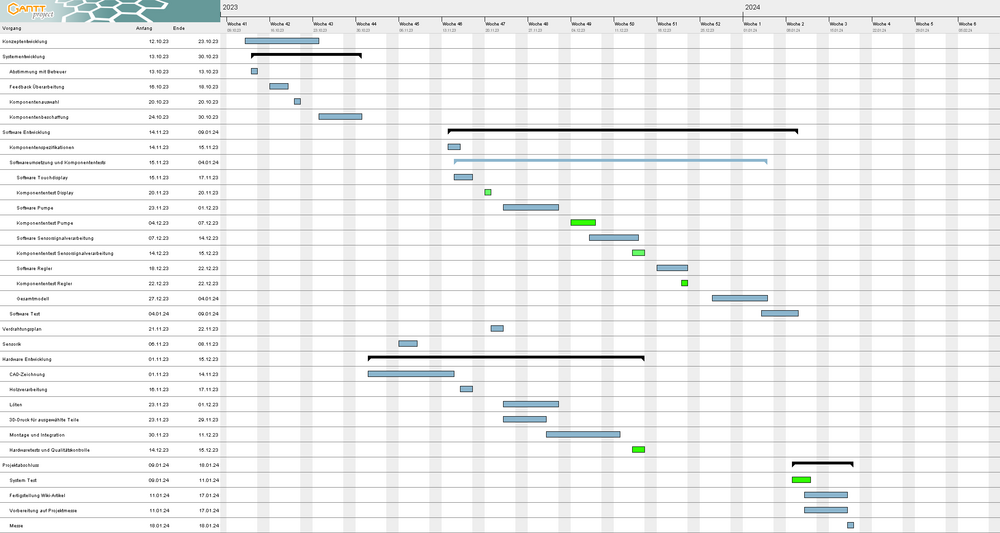
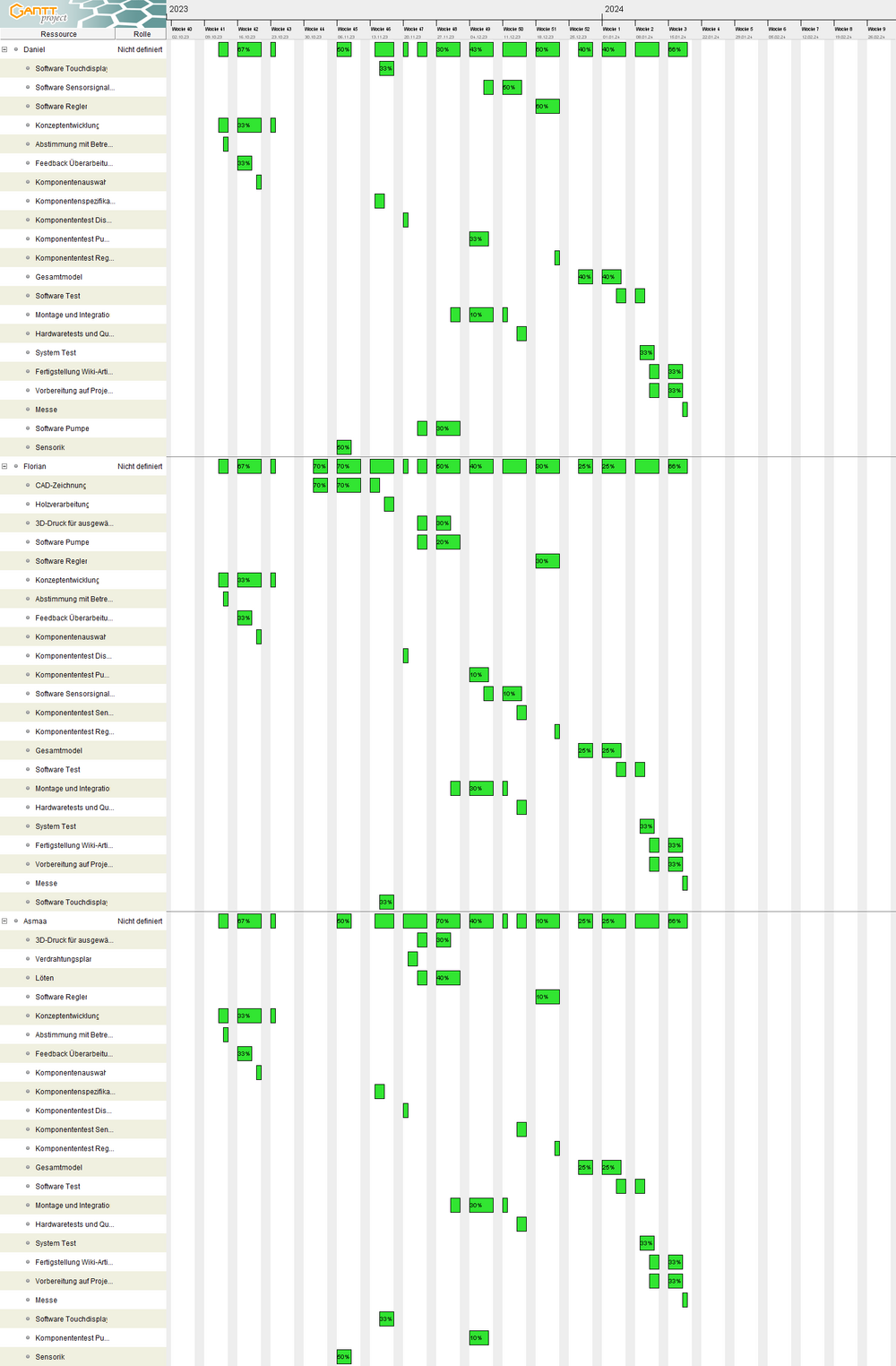
In Abbildung 27 ist die Gantt-Chart zur Visualisierung der Aufgaben und Meilensteine dargestellt, während Abbildung 28 den Ressourcenplan zeigt.
Projektdurchführung
| Nummer | Herausforderung | Lösung |
| 1 | Projektfindung | Ideensammlung, Brainstorming: automatische Müllsortierung verworfen Idee einer Pumpanwendung festgelegt, da verschiedene interessante Komponenten nutzbar sind |
| 2 | Projektplan | Planung der Durchführung des Projektes, Erstellung Gantt-Diagramm |
| 3 | Anforderungen festlegen | Entscheidung zur Wägezelle und Peristaltikpumpe, Implementierung eines Reglers |
| 4 | Entwurf | Verwirklichung der Idee in technischem und funktionalem Systementwurf |
| 5 | Organisation/Auswahl benötigter Bauteile | Bestellung Peristaltikpumpe, Wägezelle, HX711 24bit ADU Touchdisplay, Arduino, Kunststoffschlauch bereits vorhanden |
| 6 | Hardwareentwicklung | Konstruktion mittels CAD, u.A. Anordnung der Komponenten, Platzbedarf, Verdrahtungsplan |
| 7 | Softwareentwicklung | Komponentenspezifikationen, Programmablaufplan |
| 8 | Hardwareumsetzung | Fertigung Holzgehäuse, 3D-Druck (FDM), Lackierung Verkabelung, Löten, Zusammenbau |
| 9 | Softwareumsetzung | Programmierung einzelner Komponenten, Reglerauslegung, Erstellung Gesamtmodell |
| 10 | Tests | Komponententests, Kalibrierungstests, Genauigkeitstests, Test Gesamtprojekt |
| 11 | Dokumentation | Videodreh, Plakaterstellung, Dokumentation hier im Wiki |
YouTube Video
Literatur
→ zurück zur Übersicht: WS 22/23: Angewandte Elektrotechnik (BSE)
- ↑ 1,0 1,1 1,2 Schiessle, E. (2010): Industriesensorik. Vogel Buchverlag. ISBN: 978-3-8343-3076-5.
- ↑ Artikel über Dehnungsmessstreifen
- ↑ 3,0 3,1 Datenblatt des HX711 Breakout-Boards
- ↑ Berechnung der Messunsicherheit nach GUM
- ↑ Datenblatt Wägezelle