Objekterkennung mit rotierenden Infrarotsensor mit Matlab/Simulink und EV3
Autor: Thorsten Drees
Betreuer: Prof. Dr.-Ing. Ulrich Schneider
Aufgabenstellung
Begleitend zu der Vorlesung „Signalverarbeitende Systeme“ besteht die Aufgabe des Studenten darin, dass ein LEGO Mindstorm Roboter mit EV3 Brick mittels eines Sensors ein Hindernis erkennt und automatisch abbremst. Diese Notbremsung soll erfolgen, sobald sich ein Objekt 5 cm vor dem Roboter befindet. Aufgrund der Messunsicherheit wurde die Entfernung allerdings von 5 cm auf 20 cm erhöht. Als Sensor kommt in diesem Projekt ein rotierender LEGO Infrarot Sensor zum Einsatz. Die Programmierung soll in Matlab und/oder Simulink implementiert werden. Zudem ist ein Video zu erstellen, welches die Funktionalität demonstriert.
Projektplan
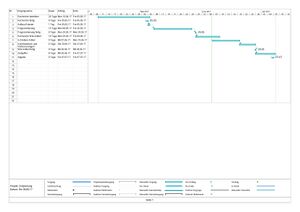
Zur zeitlichen Planung des Projekts wurde ein Gantt Chart mit MS Project 2016 erstellt. Dieses ist in Abbildung 1 zu sehen.
Primärsensor

Als Sensor für die Distanzmessung kommt der Lego EV3 Infrarot Sensor zum Einsatz. Dieser Sensor hat drei Funktionen: • IR proximity Sensor • IR seeker Sensor • IR remote control Receiver Für dieses Projekt wird der Sensor als „IR proximity Sensor“ eingesetzt. In diesem Modus bestimmt der Sensor eine relative Distanz zu einem vor ihm liegenden Objekt. Als Ausgabe liefert der Sensor einen Wert von 0 (sehr nah) bis 100 (maximale Entfernung). Implementiert ist dieser Sensor als digitaler Sensor. Das bedeutet, dass der Sensor einen kleinen 8-bit Mikrocontroller integriert hat, welcher über den UART-Bus mit dem EV3-Brick kommuniziert.
Funktionsweise des Sensors
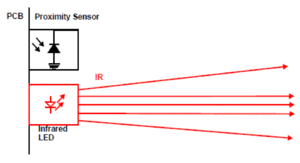
Der Sensor besteht grundlegend aus zwei Bauteilen. Zum einen besteht der Sensor aus einer infraroten LED und zum anderen aus einer Fotodiode. Die Infrarot-LED sendet einen Infrarotlichtstrahl auf ein Objekt aus. Ein Teil des ausgesendeten Lichtes wird vom Objekt reflektiert und von der Fotodiode empfangen. Die Intensität des reflektierten Lichtes ist dabei umgekehrt proportional zum Quadrat der Distanz. Die vom optischen Sensor erzeugten analogen Spannungswerte werden durch den AD-Wandler des Sensors in Digitalwerte umgewandelt. Zudem findet im Mikrocontroller die Vorverarbeitung statt, indem die Werte auf Entfernungswerte von 0-100 normiert werden. Da dieser Sensor nicht nach der Triangulation als Messmethode arbeitet sondern nach der reflektierten Lichtmenge, treten je nach Oberfläche und Farbe des Objektes stark unterschiedliche Entfernungswerte auf. Die höchste Sensibilität hat der eingesetze optische Sensor bei einer Wellenlänge von ca. 900 nm und es wird alle 50 mS eine Messung durchgeführt. Das schließt Störeinflüsse durch Umgebungslicht nahezu aus. Abbilung 3 Zeigt dazu schematisch die Funktionsweise falls sich kein Objekt vor dem Sensor befindet. [3]
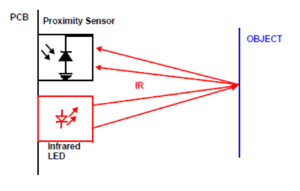
Sobald sich ein Objekt vor dem Sensor befindet erfasst die Fotodiode das reflektierte Infrarotsignal.Dies ist in der Abbildung 4 zu sehen.
Rohsignale des Sensors
Der eigentliche Infrarotsensor, also der optische Sensor (Fotodiode), gibt analoge Spannungswerte aus. Leider war es nicht möglich hierzu eine Kennline des Sensors zu erhalten. Die Rohsignale des fertigen LEGO Infrarotsensors bestehen aus int8 Werten von 0-100. Die Ausgabe erfolgt über den UART-Bus auf pin 5 und 6.
Signalvorverarbeitung
Bei dem verwendeten Sensor handelt es sich um einen digitalen Sensor welcher vorverarbeitete Daten überträgt.
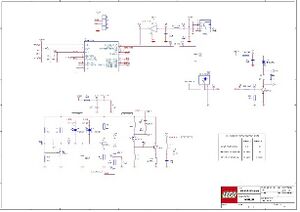
Durch den optischen Sensor (Fotodiode) wird die Intensität des reflektierten Lichtes, welches umgekehrt proportional zum Quadrat der Distanz ist, in eine Spannung gewandelt. Diese Spannung wird durch den ADU in einen digitalen Wert umgesetzt und im Mikrocontroller auf einen relativen Distanzwert von 0-100 normiert. Die dafür eingesetzte Kennlinie ist leider nicht verfügbar. Der Schaltplan auf welchem auch der eingesetze Microcontroller gezeigt ist, ist in Abbildung 5 zu sehen.
Analog-Digital-Umsetzer
Umsetzung der analogen Signale
Die Analogwerte werden innerhalb des Sensors mittels eines Microcontrollers mit der Bezeichnung STM8S103F3 umgesetzt.
Eingesetzer ADU
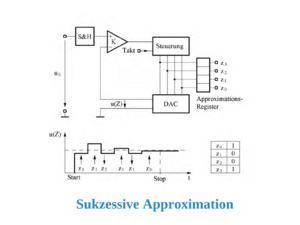
Bei diesem Microcontroller kommt ein ADU nach dem Prinzip der sukzessiven Approximation zum Einsatz. Die genauen Daten des ADU sind folgende:
- 10-bit successive approximation A/D converter (ADC1) with up to 5 external multiplexed input channels
- Input voltage range: 0 to VDD
- Conversion time: 14 clock cycles
- Single and continuous and buffered continuous conversion modes
- Buffer size (n x 10 bits) where n = number of input channels
- Scan mode for single and continuous conversion of a sequence of channels
- Analog watchdog capability with programmable upper and lower thresholds
- Analog watchdog interrupt
- External trigger input
- Trigger from TIM1 TRGO
- End of conversion (EOC) interrupt
Die AD-Wandler, wie der hier eingesetzte, funktionieren nach dem folgenden Prinzip: Das analoge Messsignal wird in n Schritten digitalisiert, wobei die Genauigkeit bei jedem Schritt um 1 Bit steigt. Bei jedem Schritt wird die Eingangsspannung mit einer Referenzspannung verglichen, die durch einen DA-Wandler erzeugt wird. Je nachdem, ob die Eingangsspannung größer oder kleiner als die Spannung des DA-Wandlers ist, wird die Referenzspannung im nächsten Schritt um die halbe Schrittweite des letzten Schrittes nach oben oder nach unten verändert. Dadurch nähert sich die Spannung des DA-Wandlers immer mehr der Eingangsspannung an. Zum Schluss, wenn das letzte Bit des DA-Wandlers gesetzt ist, entspricht der Wert des DAUs ungefähr der Eingangsspannung. [4]
Gründe für diesen ADU
Gründe, welche für diesen ADU sprechen, gibt es einige. Zum einen die hohen Abtastraten im Millisekundenbereich. Zudem sorgt die konstante Umsetzzeit für eine genaue Messung. Der Implementierungsaufwand bei dieser Art von DAUs ist zudem gering und die Kosten niedrig. Das Prinzip der sukzessiven Approximation eignet sich außerdem hervorragend zur Nachbildung per Software.
Bussystem
Bussystem zwischen Sensor und Mikrocontroller
Zwischen dem Sensor und dem EV3 Brick kommt ein UART-Bus zum Einsatz. Dabei kommuniziert der im Sensor integrierte Microcontroller über den UART-Bus auf Pin 5 und 6 mit dem EV3 P-Brick. Der Microcontroller mit der UART-Schnittstelle ist in Abbildung 7 gezeigt.
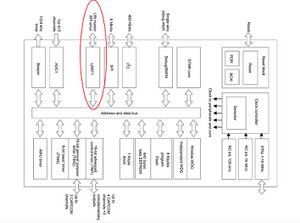
Funktionsweise des Bussystems
UART steht für Universal Asynchronous Receiver Transmitter. Diese digitale serielle Schnittstelle ist im Fall dieses EV3-Sensors als Funktionsblock eines höherintegrierten Bauteiles (hier der STM8S103F3 Mikrocontroller) ausgeführt. Die verwendete UART-Schnittstelle dient zum Senden und Empfangen von Daten über eine Datenleitung. Die Daten werden als serieller digitaler Datenstrom mit einem fixen Rahmen übertragen, der aus einem Start-Bit, fünf bis maximal neun Datenbits, einem optionalen Parity-Bit zur Erkennung von Übertragungsfehlern und einem Stopp-Bit besteht. Bei der hier verwendeten UART-Kommunikation werden ein Start-Bit, 8 Daten-Bits, ein Stopp-Bit und kein Parity-Bit eingesetzt. [1] Durch die asynchrone Betriebsweise wird kein eigenes Taktsignal auf einer Übertragungsleitung benötigt. Stattdessen synchronisiert sich der Empfänger über die Länge des Rahmens. Dieser ist gegeben durch die Schaltflanke von Start- und Stopp-Bit, sowie die eingestellte Baudrate (entspricht der Bitrate). Der Beginn einer Übertragung kann zu beliebigen Zeitpunkten mit dem Start-Bit erfolgen, daher wird diese serielle Schnittstelle als asynchron bezeichnet. Um eine Synchronisation gewährleisten zu können, ist die Anzahl der übertragbaren Bits eingeschränkt. [6]
Digitale Signalverarbeitung
Verarbeitungsschritte im Simulink-Modell
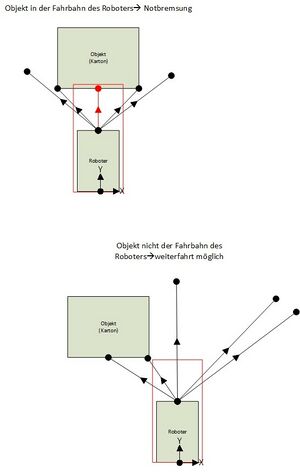
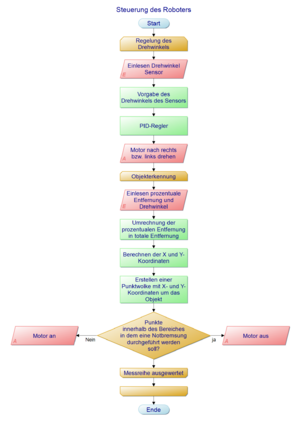
Der Ablauf des Programmes zur Robotersteuerung ist im Programmablaufplan (Abbildung 9) gezeigt. Das MATHLAB Simulink-Modell befindet sich im SVN [1]. Die digitale Signalverarbeitung gliedert sich bei diesem Projekt einmal in die Reglung zum Schwenken des Sensors und in die Objekterkennung mittels des Infrarotsensors. Die Regelung des Schwenkwinkels des Infrarotsensors wird durch einen PI-Regler übernommen. Die Regelstrecke hat ein Integrierendes Verhalten. Als Soll-Wert dient ein Sinus mit der Amplitude von 35. Diese 35 entsprechen einem maximalen Soll-Winkel von 35 °. Über den Encoder des EV3-Motors wird der Ist-Winkel auf den Regler zurückgeführt. Zur Objekterkennung wird die relative Entfernung, welche vom Infrarotsensor ausgegeben wird, mittels Lookup-Table in eine absolute Entferung umgerechnet. Im Anschluss kann zusammen mit dem Winkel des Encoders eine Punktewolke um ein erkanntes Objekt gelegt werden. Sobald ein Punkt dieser Wolke einen X-Wert unter 20 cm bzw. einen Y-Wert unter 20 cm aufweist, wird eine Notbremsung durchgeführt. Abbildung 8 dient zur schematischen Veranschaulichung der eingesetzten Logik hinter der Objekterkennung
Empfindlichkeit des Sensors
Der Infrarotsensor macht im Proximity Mode alle 50 mS eine Messung. Die relative Wellenlängenempfindlichkeit ist in der Abbildung 10 dargestellt. Wie man sieht, ist der Sensor um 900 nm am empfindlichsten.
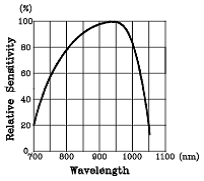
Da der Sensor nur relative Entfernungswerte von 0-100% ausgibt, kann hier die Messunsicherheit nicht angegeben werden. Das geschieht am Ende dieses Artikels, nachdem durch eine erstelle Lookup-Table die relativen Werte in absolute Entfernungswerte umgerechnet wurden.
Darstellung der Ergebnisse
Die Aufgabe der Objekterkennung sowie der Notbremsung wird erfüllt. Der Roboter stoppt vor dem Objekt, falls es sich in der Fahrbahn des Roboters befindet. Die Entfernung zum Objekt liegt dabei zwischen 14 cm und 18 cm, mehr dazu im Unterpunkt Messunsicherheit. Falls das erkannte Objekt nicht in der Fahrbahn des Roboters ist, wird das erkannt und der Roboter fährt an dem Objekt vorbei. Es ist anzumerken, dass die Messung des Abstandes extrem von der Oberfläche und der Farbe des Objektes abhängig ist. Dies liegt an dem eingesetzen Verfahren zur Ermittlung der Entfernung. Hier besteht auch das größte Optimierungspotenzial. Durch den Einsatz eines Infrarot-Sensors, welcher die Entfernung nach dem Triangulationsverfahren bestimmt, kann die Objekterkennung weitgehend unabhängig von Farbe und Oberfläche des Objektes geschehen.
Fehler in den einzelnen Verarbeitungsschritten
In der Signalverarbeitungskette können bei diesem Projekt an verschiedenen Verarbeitungsschritten Fehler auftreten. Beispielsweise können bei der AD-Umwandlung folgende Fehler auftreten:
- Quantisierungsfehler
- Amplitudenfehler
- Linearitätsfehler
- Phasenfehler
- Quantisierungsrauschen
Weitere Fehler kommen von der Ungenauigkeit bei der Umrechnung der relativen Entfernung mittels der eingesetzten Lookup Table sowie der Winkelmessung zustande. Zudem kommt es zu Rundungsfehlern bei der Berechnung der X- und Y-Koordinaten. Bevor die Notbremsung eingeleitet wird, muss vorher eine komplette Messreihe aufgenommen worden sein während der sich der Roboter weiter bewegt. Das führt dazu, dass dieser nicht bei genau 20 cm stoppt sondern die Entfernung zum Objekt immer unter 20 cm liegt.
Messunsicherheit des Infrarot-Sensors bei der Abstandsmessung
Um die Genauigkeit der absoluten Entfernungsmessungen einschätzen zu können, wurde ein Messplatz aufgebaut. Als Objekt wurde ein weißer Karton verwendet. Die Entfernung zum Karton wurde mittels eines Maßbandes auf dem Boden ermittelt. Nun wurde der Roboter in verschiedenen Abständen zum Karton positioniert. Diese Entfernung, sowie die mittels Infrarot Sensor ermittelte Entfernung und die absoluten und relativen Fehler sind in Tabelle 1 zu sehen.
Tabelle 1: Bestimmung Messunsicherheit für die Entfernungsmessung
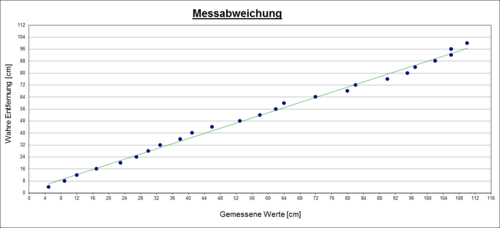
| Messung Nr. | Entfernung [cm] | Entfernung gemessen [cm] | Absoluter Fehler [cm] | Relativer Fehler [%] |
| 1 | 4 | 5 | -1 | -25 |
| 2 | 8 | 9 | -1 | -12 |
| 3 | 12 | 12 | 0 | 0 |
| 4 | 16 | 17 | -1 | -6,25 |
| 5 | 20 | 23 | -3 | -15 |
| 6 | 24 | 27 | -3 | -15 |
| 7 | 28 | 30 | -2 | -12,5 |
| 8 | 32 | 33 | -1 | -7,14 |
| 9 | 36 | 38 | -2 | -3,13 |
| 10 | 40 | 41 | -1 | -5,56 |
| 11 | 44 | 46 | -2 | -2,5 |
| 12 | 48 | 53 | -5 | -4,55 |
| 13 | 52 | 58 | -6 | -10,42 |
| 14 | 56 | 62 | -6 | -11,54 |
| 15 | 60 | 64 | -4 | -10,71 |
| 16 | 64 | 72 | -8 | -12,5 |
| 17 | 68 | 80 | -12 | -17,65 |
| 18 | 72 | 82 | -10 | -13,89 |
| 19 | 76 | 90 | -14 | -18,42 |
| 20 | 80 | 95 | -15 | -18,75 |
| 21 | 84 | 97 | -13 | -15,48 |
| 22 | 88 | 102 | -14 | -15,91 |
| 23 | 92 | 106 | -14 | -15,22 |
| 24 | 96 | 106 | -10 | -10,42 |
| 25 | 100 | 110 | -10 | -10 |
| Ø Absoluter Fehler[cm] | -6,32 | |||
| Ø Relativer Fehler[%] | -11,27 |
Messunsicherheit / Vertrauensbereich bei der Notbremsung
Zudem wurde eine weitere Messreihe zu dem Abstand zum Objekt nach der Notbremsung aufgenommen. Dabei ist der Messaufbau derselbe wie bei den vorherigen Messungen. Der Roboter ist bei diesen Messungen von verschiedenen Entfernungen auf das Objekt zugefahren. Nach der Durchführung des David-Hartley-Pearson-Test steht fest das es sich um eine Normalverteilung handelt. Daher ist es möglich den Vertrauensbereich für den Mittelwert zu einem geforderten Vertrauensniveau, also der geforderten statistischen Sicherheit, anzugeben. Ausgehend von einer Betriebsmessung wird ein Vertrauensniveau von 95% angenommen.[9] In der Abbildung 12 ist dazu der Vertrauensbereich, die Standartabweichung, der Mittelwert sowie der vorgegeben Sollwert von 20 cm abgebildet.
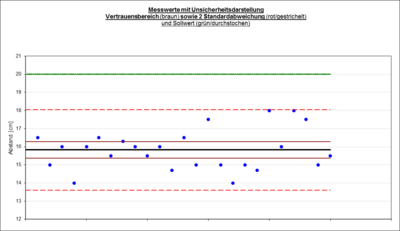
Wie zu sehen ist, liegt der Sollwert außerhalb des Vertrauensbereichs. Das liegt daran, dass der Roboter erst eine Messreihe (ein Schwenk des Sensors) warten muss bevor er Ergebnisse vorliegen hat. Es liegt also ein systematischer Fehler von -4,17 cm vor. Dieser sollte zukünftig im Modell berücksicht werden um innerhalb des Vertrauensbereichs zu arbeiten. Die gesamte statistische Auswertung in im SVN [2] hinterlegt. Der durchnittliche relative Fehler liegt bei 20,86 %.
Lessons Learned
Durch die Bearbeitung dieses Projektes und der Auseinandersetzung mit den Themen wie den Hardwarearchitekturen des Sensors und des Bricks lernte man diese theoretisch kennen und sah sofort die praktische Anwendung. Zudem konnte man die praktische Anwendung des in der Vorlesung besprochenen Analog-/Digital-Umsetzers nach dem Prinzip der sukzessiven Approximation in der Praxis sehen. Bei der Umsetzung des Simulink Programmes lernte man mögliche Strategien zur Objekterkennung sowie die praktische Anwendung dieser kennen. Auch konnte man das Wissen aus der Reglungstechnik anwenden, da zum Rotieren des Sensors eine Regelung eingesetzt werden musste. Zuletzt konnte man durch die Auswertung der Messunsicherheiten den systematischen Fehler bestimmen und so ist es nun möglich die Messung bzw. den Bremsweg in Zukunft genauer zu gestalten.
Youtube-Video
Das Ergebnis des Projektes wurde in einem Video festgehalten, das unter folgendem Link zu erreichen ist: [3]
Einzelnachweise
[1] https://education.lego.com/de-de/support/mindstorms-ev3/developer-kits Abgerufen am 20.05.2017
[2] http://www.eetimes.com/document.asp?doc_id=1272536 Abgerufen am 25.05.2017
[3] http://www.g9toengineering.com/AllSaints/infraredproximity.htm Abgerufen am 01.06.2017
[4] http://www.vias.org/mikroelektronik/adc_succapprox.html Abgerufen am 01.06.2017
[5] Skript Signalverarbeitende Systeme; Prof. Dr.-Ing. Ulrich Schneider; 2017
[6] https://de.wikipedia.org/wiki/Universal_Asynchronous_Receiver_Transmitter Abgerufen am 09.05.2017
[7] http://www.st.com/en/microcontrollers/stm8s103f2.html Abgerufen am 09.05.2017
[8] https://sh-s7-live-s.legocdn.com/is/image/LEGO/45509?$PDPDefault$ Abgerufen am 09.06.2017
[9] Rainer Parthier, Messtechnik,Grundlagen und Anwendungen der elektrischen Messtechnik, 8. Auflage, 2016,Wiesbaden, Springer Fachmedien
→ zurück zum Hauptartikel: Signalverarbeitende Systeme SoSe2017