Stopplinien-Verhalten: Unterschied zwischen den Versionen

Version vom 7. Juni 2020, 17:15 Uhr

→ zurück zur Übersicht: SDE-Team_2019/20
→ zurück zur Übersicht: SDE-Team_2020/21

Bearbeiter: Yanick Christian Tchenko
Autoren: Hagen Heuer, Tim Kruse
Betreuer: Prof. Schneider

Einleitung

In dieser Aufgabestellung ist die Zielsetzung, das Verhalten des Fahrzeugs an Stopplinien entsprechend den Anforderungen im Lastenheft zu implementieren. Das Fahrzeug muss nach dem Lastenheft im Falle der Erkennung einer Haltelinie immer langsamer fahren. Befindet sich es an der Stopplinie, dann muss es zwei Sekunden halten und anschleißend weiterfahren.

Anforderungen

Im Lastenheft des Projets Carolo Cup wird die Steuerung des Verhaltens des Fahrzeugs an der Stopplinie genau so wie in der folgenden Abbildung gefordert:

Abb. 1: Lastenheft

Es entstand demnach das untere Pflichtenheft:

Abb. 2: Pflichtenheft

Folgende Anforderungen können festgelegt werden und im späteren Projekt berücksichtigt werden.

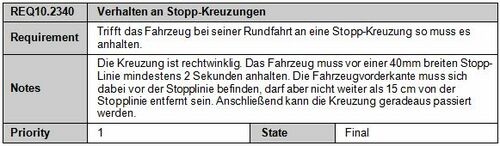
Trifft das Fahrzeug bei seiner Rundfahrt an eine Stopp-Kreuzung, so muss es 15 cm vor der Stopplinie anhalten.
Während das Fahrzeug auf die Stopplinie zufährt, muss die Geschwindigkeit des Fahrzeugs gedrosselt werden.
Das Fahrzeug muss vor der Stoppline halten und 2 Sekunden warten.
Nach der Wartezeit muss das Fahrzeug die Kreuzung passieren, ohne das die Stopplinie ein weiteres Mal erkannt wird.
Die Implementierung erfolgt in Matlab-Simulink.

Konzept

Als Basis für die Implementierung diente die vorhandene Matlab-Funktion für das Verhalten an Stoppkreuzungen. Beim Testen dieser Funktion viel unter anderem auf, dass diese nicht lauffähig ist. Außerdem war die Implementierung der Weiterfahrt nach einer Stopplinie fehlerhaft, da das Fahrzeug die vorherige Stopplinie erneut erkennen würde.

Daher wurde ein neues Konzept erstellt, in dem Teile der ursprünglichen Idee berücksichtigt wurden. Zudem wurde die Matlab-Funktion um weitere Ein- und Ausgänge erweitert.

Eingänge:

Stopplininenflag
Stopplinienabstand
Zykluszahl
Zustand

Ausgang:

Geschwindigkeitsfaktor
Zykluszahl
Zustand

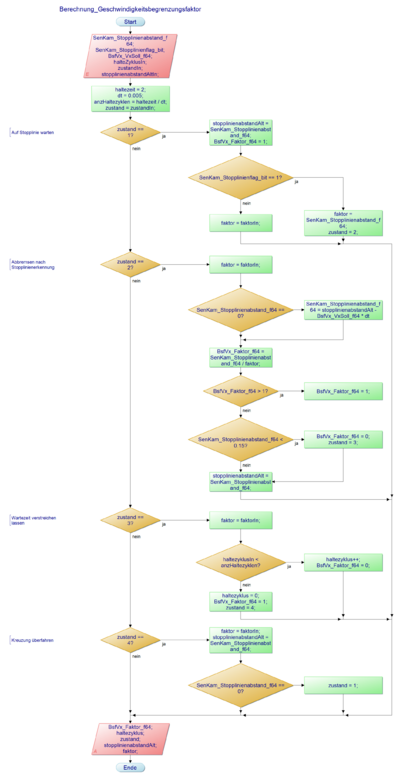
Der Programmablaufplan des neuen Konzeptes ist im Folgenden erklärt.

Abb. 3: Progammablaufplan

Zu Beginn werden Variablen eingelesen und initialisiert. Anschließend erfolgt die Abfrage der einzelnen Cases. Das Programm wird hierbei in vier Cases unterteilt.

Case 1 (Zustand == 1)
In Case 1 werden zunächst Variablen an den Ausgang übergeben. Anschließend wird abgefragt, ob das Stopplinienflag Eins ist. Trifft dies zu wird das interne Stopplinienflag gesetzt und der Stopplinienabstand in der Variable Faktor gespeichert. Anschließt wird der Zustand auf 2 gesetzt. Wurde keine Stopplinie gefunden, so werden die Variablen überschrieben und der Zustand nicht gewechselt.

Case 2 (Zustand == 2)
Ist der Case 2 aktiv, so werden zunächst Variablen mit dem vorherigen Wert überschrieben. Wenn das Stopplinienflag intern Eins ist, wird dieses mit dem selben Wert überschrieben. Ist der Stopplinienabstand Null, so wurde die Stopplinie verloren und der Stopplinienabstand wird mit Hilfe der Geschwindigkeit und dem Faktor sowie der Simulationszeit interpoliert. Durch die Rechnung Stopplinienabstand = Stopplinienabstand alt - Geschwindigkeit * 0,005 wird die zurückgelegte Strecke im letzten Programmzyklus vom alten Abstand subtrahiert. Somit ergibt sich der neue Stopplinienabstand. Anschließend wird die neue Geschwindigkeit errechnet und der Zustand auf Zwei gesetzt. Falls die errechnete Geschwindigkeit größer Eins sein sollte, wird der Faktor auf Eins begrenzt. Wenn der Stopplinienabstand kleiner 15 cm sein sollte, werden die Motoren abgeschaltet und der Zustand auf Drei gesetzt.

Sollte das Stopplinienflag intern nicht gesetzt sein, so wird dieses wieder auf Null gesetzt, das Fahrzeug auf Sollgeschwindigkeit beschleunigt und der Zustand auf 1 gesetzt.

Zuletzt wird noch der Stopplinienabstand gesichert.

Case 3 (Zustand = 3)
In Case 3 werden zunächst die Variablen gesichert. Anschließend wird der aktuelle Haltezyklus mit dem vorgegebenen Haltezyklus verglichen. Mit Hilfe dieser Haltezyklen kann die Haltezeit erfasst werden, da die Simulationszeit 0,005 Sekunden beträgt. Solange die Haltezyklen geringer sind wie die vorgegebene Zahl, werden diese um eins addiert und der Case 3 nicht verlassen. Im anderen Fall wird Fahrzeug wieder beschleunigt und es wird in den Case 4 gewechselt.

Case 4 (Zustand = 4)
Im vierten Case wird der Abstand zur Stopplinie abgefragt. Falls dieser größer Null ist, soll das Fahrzeug weiter fahren und den Case nicht verlassen. Falls der Abstand zur Stopplinie Null ist, soll in den Case 1 gewechselt werden und dort auf eine neue Stopplinie reagiert werden.

Falls kein Case ausgewählt wurde, soll in den vorherigen Case gewechselt werden und das Fahrzeug weiter fahren.

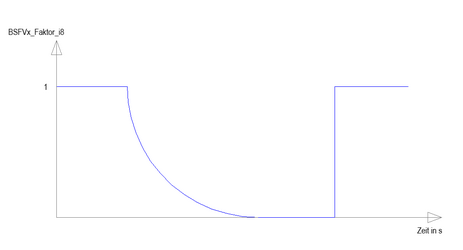
Abb. 4: Verhalten der Geschwindigkeit

Ziel ist es das folgende Verhalten, wie in Abbildung 4 zu sehen, zu erreichen. Der Geschwindigkeitsfaktor hat den Wert 1 angenommen und das Fahrzeug fährt mit konstanter Geschwindigkeit. Wird eine Stopplinie erkannt, so soll das Fahrzeug verzögern bis es zum Stillstand kommt. Nach den zwei Sekunden Wartezeit soll das Fahrzeug wieder beschleunigen, weshalb der Geschwindigkeitsfaktor den Wert 1 annimmt.

Umsetzung und Ergebnis der Simulationsumgebung

Autoren: Hagen Heuer, Tim Kruse

Die Umsetzung der Implementierung erfolgt wie bereits erwähnt im Offline-Modell mit Hilfe von Simulink und Matlab c-Code. Hierfür wurde eine Matlab-Funktion eingefügt und anhand des Programmablaufplans programmiert. Da die Funktion in jedem Zyklus neu aufgerufen wird, gehen die vorherigen Werte der Variablen verloren. Dies musst allerdings für zwei Werte verhindert werden, da diese im nächsten Zyklen von Bedeutung sind. Somit wurde das Ausgangssignal über einen Memory-Baustein an den Eingang zurück gegeben. Außerdem wurden im Memory-Baustein passende initialwerte hinterlegt, da im ersten Aufruf der Funktion noch keine Werte errechnet wurden.
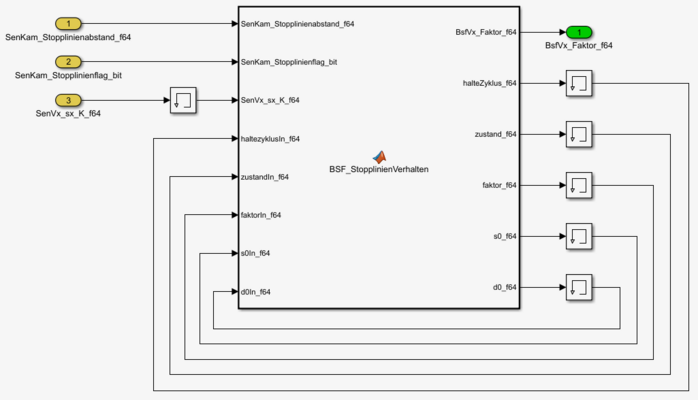
Die Matlab-Funktion ist zudem in Abbildung 5 zu sehen.

Abb. 5: Matlab-Funktion

Das Ergebnis des Stopplinienverhalten wird in der nachfolgenden Abbildung dargestellt. Im ersten Diagramm ist das Stopplinienflag zu sehen, welches bei Detektion einer Stopplinie auf Eins wechselt.

Im zweiten Diagramm ist der dazugehörige Stopplinienabstand zu sehen. Diese ist solange Null bis eine Stopplinie erkannt wurde. Die Stopplinie kann ab einem Abstand von 1 Meter oder weniger erfasst werden. In der Kurve ist zudem gut zu erkennen, dass das Fahrzeug beginnt zu verzögern, da der Abstand nicht Linear abnimmt.
Funktionstest ergaben, dass es zu einem Verlust der Stopplinie kommen kann. Für diesen Fall wurde eine Interpolation des Stopplinienabstands implementiert. Hierdurch kann auf Basis der Geschwindigkeit der Stopplinienabstand errechnet werden.

Im letzten Diagramm wird die errechnete Geschwindigkeit ausgegeben. Auf diese wird der Faktor aus der Matlab-Funktion addiert. Auch in dieser Kurve ist gut zu sehen, dass das Fahrzeug verzögert. Wenn der Abstand 15 cm oder weniger beträgt, werden die Motoren abgeschaltet, da der Faktor auf Null abfällt.

Nach der zweisekündigen Wartezeit beschleunigt das Fahrzeug wieder und der Abstand zur Stopplinie nimmt linear weiter ab. Erreicht dieser Null, so wird die Stopplinie überfahren und das Stopplinienflag wird wieder Null.

Das Verhalten wird zudem im nebenstehenden Video ersichtlich.

Abb. 6: Ergebnis

Komponententest

Hier werden die verschiedenen entwickelten Komponente getestet. Die Testergebnisse ergaben nach bestimmten Eingaben die in der unteren Tabelle zu sehenden numerische Resultate.

ID	Testfallbeschreibung	Eingänge(`SenKam_StoplinieAbst_f64`, `SenKam_StoplinieFlag_bit`)	Ausgang(`BSFVx_Faktor_i8`)	Erwartetes Ergebnis	Testergebnis	Testperson	Datum
1	Das Fahrzeug fährt normal, wenn keine Stopplinie erkannt wurde.	SenKam_StoplinienFlag_bit = 0, SenKam_StoplinienAbst_f64 = 0	1	Vollgas	1	Tchenko (mit Zustimmung von Prof. Schneider)	15.11.2019
2	Trifft das Fahrzeug bei seiner Rundfahrt an eine Stopp-Kreuzung so muss es 10cm vor der Stopplinie anhalten	SenKam_StoplinienFlag_bit = 1, SenKam_StoplinienAbst_f64 <= 10% Max_Abstand	0	Fahrzeug Stoppt	0	Tchenko (mit Zustimmung von Prof. Schneider)	15.11.2019
3	Das Fahrzeug fährt weiter, wenn keine Stopplinie erkannt wurde.	SenKam_StoplinienFlag_bit = 0, SenKam_StoplinienAbst_f64 existiert	1	Nicht plausibeler Fall. (Da keine Stopplinie erkannt wurde)	1	Tchenko (mit Zustimmung von Prof. Schneider)	15.11.2019
4	Das Fahrzeug muss im Bereich zwischen 0.1m und 1m vor der Stopplinie immer langsamer fahren.	SenKam_StoplinienFlag_bit = 1, 0<SenKam_StoplinienAbst_f64<=10	0<`BSFVx_Faktor_i8`<1 (Linieare Änderung)	Bremsen	0<`BSFVx_Faktor_i8`<1 (Linieare Änderung)	Tchenko (mit Zustimmung von Prof. Schneider)	15.11.2019
5	Das Fahrzeug muss bei Srtopplinienerkennung im Bereich weiter als 1m weiter normal fahren.	SenKam_StoplinienFlag_bit = 0, SenKam_StoplinienAbst_f64>10	`BSFVx_Faktor_i8` = 1	Nicht unterbrochene Fahrt	`BSFVx_Faktor_i8` = 1	Tchenko (mit Zustimmung von Prof. Schneider)	15.11.2019

Die Abbildung "Simulationsergebnis unter Berücksichtigung unterschiedlicher Testfälle" steht ferner graphisch dar, wie sich die Werte des BSFVx_Faktor_i8 in Abhängigkeit der simulierten Werte für SenKam_StoplinienFlag_bit und SenKam_StoplinienAbst_f64 verändert. Dies erfolgt unter Anwendung des entwickelten Moduls zur Steeurung des Fahrzeugsverhaltens an der Stopplinie. (Siehe Abb. 4)

Diskussion

Design-Review des Konzept

In Abbildung 4 fehlt die Beschriftung der Achsen.

Gelöst am 06.06.2020

Warum woher kommt die 0.8, durch die der Abstand zur Stopplinie geteilt wird?

Behoben am 07.06.2020

Hier und da finden sich Rechtschreibfehler.

Review: Marius Köhler, 02.06.2020