DSB18: Start- und Stopplinienerkennung: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
Keine Bearbeitungszusammenfassung |
||
| Zeile 82: | Zeile 82: | ||
</syntaxhighlight> | </syntaxhighlight> | ||
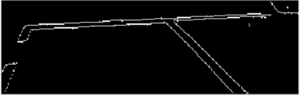
Darauf aufbauend wir durch die Verwendung des Sobel-Operators die Kanten innerhalb des Bildausschnitts extrahiert. Dieses resultierende Kantenbild wird ebenfalls in der Figur gezeigt. [[Datei:Sobel.png|mini|Mittels Sobel-Operator extrahierte Kanten, welche aus dem ROI des Graustufenbildes gewonnen wurden.]] | Darauf aufbauend wir durch die Verwendung des Sobel-Operators die Kanten innerhalb des Bildausschnitts extrahiert. Dieses resultierende Kantenbild wird ebenfalls in der Figur gezeigt.[[Datei:Sobel.png|mini|Mittels Sobel-Operator extrahierte Kanten, welche aus dem ROI des Graustufenbildes gewonnen wurden.]] | ||
<syntaxhighlight lang="matlab" line='line'> | <syntaxhighlight lang="matlab" line='line'> | ||
| Zeile 118: | Zeile 118: | ||
</syntaxhighlight> | </syntaxhighlight> | ||
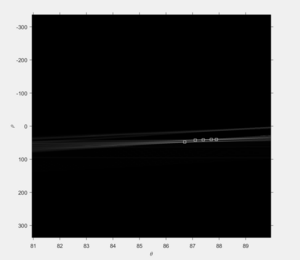
[[Datei:HoughPeaks.png|mini|Parameterraumdrastellung der Hough-Transformation mit den ermittelten Maxixma (weiße Kästchen).]] | |||
Um die Maxima der Hough-Transformation zu identifizieren, wird die Funktion <code>houghpeaks</code> verwendet. Dazu wird der Funktion das Ergebnis der Hough-Transformation in Matrixform sowie eine maximale Anzahl an zu ermittelnden Maxima übergeben. Zudem wird ein Schwellwert zur Definition eines Maximums vorgegeben. Hier wird der Schwellwert als 30<math>\,</math>% des globalen Maximums der Hough-Transformation gewählt. Die Funktion gibt anschließend die Reihen und Spalten Indices der gefundenen Maxima innerhalb der Hough-Transformationsmatrix zurück.<ref>[https://de.mathworks.com/help/images/ref/houghpeaks.html''MathWorks Documentation: houghpeaks''] Website der MathWorks Dokumentation zur Identifikation von Spitzen einer Hough-Transformation. Abgerufen am 30. Juni 2018.</ref> | Um die Maxima der Hough-Transformation zu identifizieren, wird die Funktion <code>houghpeaks</code> verwendet. Dazu wird der Funktion das Ergebnis der Hough-Transformation in Matrixform sowie eine maximale Anzahl an zu ermittelnden Maxima übergeben. Zudem wird ein Schwellwert zur Definition eines Maximums vorgegeben. Hier wird der Schwellwert als 30<math>\,</math>% des globalen Maximums der Hough-Transformation gewählt. Die Funktion gibt anschließend die Reihen und Spalten Indices der gefundenen Maxima innerhalb der Hough-Transformationsmatrix zurück.<ref>[https://de.mathworks.com/help/images/ref/houghpeaks.html''MathWorks Documentation: houghpeaks''] Website der MathWorks Dokumentation zur Identifikation von Spitzen einer Hough-Transformation. Abgerufen am 30. Juni 2018.</ref> | ||
Version vom 3. Juli 2018, 19:55 Uhr
Autor: Stephan Marks
Betreuer: Prof. Schneider
Motivation
Eine Aufgabe beim Carolo Cup ist der "Rundkurs mit Hindernissen". Hierbei ist eine Startlinie zu überfahren und an einer Stopplinie zu halten.
Ziel
Die Start- und Stoppline soll robust erkannt und unterschieden werden.
Anforderungen
- Nutzen Sie die bestehende Aufzeichnung der Kameransicht eines Rundkurses.
- Lesen Sie diesen als Endlosschleife in Matlab ein.
- Identifizieren Sie während der virtuellen Fahrt Start- und Stopplinien mit Matlab.
- Vermeiden Sie Fehler ("false-positives").
- Optimieren Sie die Rechenzeit Ihres Algorithmus.
- Wissenschaftliche Dokumentation als HSHL-Wiki Artikel
- Softwareentwicklung nach SDE Standard in SVN
- Funktionsnachweis als YouTube-Video (vgl. Veranstaltungsregeln)
Lösungen
Einleitung
Im Sommersemester 2018 wird das Praktikum „Systementwurf“ durchgeführt. Gegenstand dieses Projekts ist ein autonomes Fahrzeug. Unter anderem soll dieses Fahrzeug selbstständig auf einem Rundkurs fahren. Neben der Erkennung der Fahrspur wird die Detektion von Stopplinien benötigt. Stopplinien sind beispielsweise in Kreuzungsbereichen vorhanden. An diesen soll das Auto gemäß der Straßenverkehrsordnung halten. Außerdem enthält der Rundkurs eine Startlinie, an welcher das Fahrzeug nicht halten soll.
Implementierung
Die Stopplinienerkennung wird anhand eines vorhandenen Videos einer Fahrt auf dem Rundkurs in Form eines MATLAB-Skripts implementiert.
Vorinitialisierungen
Zu Beginn der Bildverarbeitung werden einige Vorinitialisierungen durchgeführt. Zunächst wird das Command Window der MATLAB-Benutzeroberfläche geleert, alle geöffneten Figuren geschlossen und vorhandene Variablen gelöscht. Anschließend wird ein Region of Interest (ROI) definiert, der den für die Stopplinienerkennung relevanten Bildausschnitt beschreibt. Zuletzt wird eine Figur zur Darstellung verschiedener Ausgabebilder in einem Vollbildformat initialisiert.
clc,close all,clear varibales; % Command Window leeren, Figuren schließen, Variablen löschen
%% Vorinitialisierungen
% ROI (Region of interest)
% [xmin ymin width height]
roi = [216 225 320 100];
% Speicher für das Kantenbild in der Größe des ROI
edgeFrame = zeros(roi(1,4),roi(1,3));
% Figur in Vollbild
figure('units','normalized','outerposition',[0 0 1 1]);
hold on;
Einlesen des Videos
Zunächst wird die Videoaufnahme der Fahrt eingelesen. Dazu wird ein VideoReader-Objekt erzeugt. Das Video soll endlos abgespielt werden. Dazu wird innerhalb einer Endlosschleife zu Beginn überprüft, ob die Aufnahme noch unverarbeitete Einzelbilder (Frames) besitzt. Ist dies nicht der Fall, ist das Ende des Videos erreicht und die Abspielzeit wird auf den Beginn zurückgesetzt.
%% Video einlesen und einzelne Bilder verarbeiten
video = VideoReader('Rundkurs.mp4'); % Das Video muss sich im gleichen Ordner wie dieses Programm befinden.
% Einlesen des Videos in einer Endlosschleife
while true
if ~video.hasFrame
video.CurrentTime = 0.0;
disp('Restart Video');
end
Erkennung der Stopplienen
Um die Stopplinienerkennung durchzuführen wird aus der eingelesenen Videodatei ein Einzelbild entnommen. Dieses Bild wird innerhalb der vorinitialisierten Figur in Form eines Subplots dargestellt.
% Frame aus Video entnehmen und als Subplot anzeigen
frame_original = readFrame(video);
subplot(1,3,1)
imshow(frame_original);
title('Original')
Das Einzelbild wird zur weiteren Verarbeitung auf den ROI begrenzt und in ein Graustufenbild umgewandelt.
% Bild auf ROI begrenzen und in Grauwertbild umwandeln
frame_roi = rgb2gray(imcrop(frame_original,roi));
Darauf aufbauend wir durch die Verwendung des Sobel-Operators die Kanten innerhalb des Bildausschnitts extrahiert. Dieses resultierende Kantenbild wird ebenfalls in der Figur gezeigt.
% Grauwertbild in Kantenbild überführen und in Figur darstellen
frame_roi_edge = edge(frame_roi,'sobel','horizontal');
subplot(1,3,2)
imshow(frame_roi_edge);
title('Sobel')
Hough-Transformation
Die Fahrspuren innerhalb des vorbereiteten Kantenbildes sollen durch die Hough-Transformation detektiert werden. Die Hough-Transformation nutzt die Darstellung einer Geraden in der Parameterform
.
In dieser Darstellung beschreibt den Betrag des Ortsvektors zu der Geraden, was der Distanz vom Koordinatenursprung zu der Geraden entspricht. Der Winkel stellt den Winkel des Ortsvektors im Bezug zur x-Achse des Koordinatensystems dar. Die MATLAB-Funktion hough
zur Hough-Transformation gibt zusätzlich zu und die Parameterraumdarstellung in Matrixform zurück.
Die zu detektierenden Stopplinien zeichnen sich dadurch aus, dass diese annähernd horizontal verlaufen. Dadurch kommen ausschließlich Geraden mit einem Winkel theta in einem Intervall von
als Kandidaten für eine Stopplinie infrage. Die Intervallweite wurde experimentell ermittelt. Die MATLAB-Funktion hough bietet die Möglichkeit das Winkelintervall direkt vorzugeben, sodass nur relevante Linien zurückgegeben werden.[1]
% Transformation mit beschränkem 'Theta', sodass nur Linien in einem
% horizontalen Bereich betrachtet werden.
[H,theta,rho] = hough(frame_roi_edge,'Theta', 81:0.1:89.9);
Um die Maxima der Hough-Transformation zu identifizieren, wird die Funktion houghpeaks verwendet. Dazu wird der Funktion das Ergebnis der Hough-Transformation in Matrixform sowie eine maximale Anzahl an zu ermittelnden Maxima übergeben. Zudem wird ein Schwellwert zur Definition eines Maximums vorgegeben. Hier wird der Schwellwert als 30% des globalen Maximums der Hough-Transformation gewählt. Die Funktion gibt anschließend die Reihen und Spalten Indices der gefundenen Maxima innerhalb der Hough-Transformationsmatrix zurück.[2]
% Maxima in der Transformation ermitteln
P = houghpeaks(H,5,'threshold',ceil(0.3*max(H(:))));
Aus den gewonnen Daten werden durch die Verwendung einer weiteren Funktion letztendlich die Linien bestimmt. Dazu werden der Funktion houghlines das Graustufenbild, die Parameter und sowie die zuvor ermittelten Indices der bestimmten Maxima der Hough-Transformation übergeben. Darüber hinaus besitzt die Funktion die Möglichkeit Liniensegmente über eine Lückenfüllung miteinander zu einer Gesamtlinie zu verbinden und eine Mindestlänge der gefundenen Linie festzulegen. Ein Suchbereich für die Lückenfüllung von 20 Pixeln sowie eine Mindestlänge von 150 Pixeln liefern gewünschte Ergebnisse. Die Funktion gibt die berechneten Linien mit den Attributen eines Start- und Endpunkts sowie den Parametern und zurück.[3]
% Linien mit einer Mindestlänge ermitteln und dabei Linenstücke
% in bestimmten Berich verbinden
lines = houghlines(frame_roi_edge,theta,rho,P,'FillGap',20,'MinLength',150);
Verarbeitung der ermittelten Kandidaten
Um aus den gefundenen Linienkandidaten die letztendliche Stopplinie zu bestimmen, wird die Linie ausgewählt, welche an nahesten zur Fahrzeugfront liegt. Dadurch, dass der Ursprung einer Matrix beziehungsweise eines Bildes in MATLAB in der oberen linken Ecke definiert ist, muss die Linie gefunden werden, welche den größten Abstand zum oberen Bildrand aufweist. Bei dieser Linie handelt es sich um die gesuchte Stopplinie.
subplot(1,3,3)
imshow(frame_roi), hold on;
title('Stopplinie')
% falls Linien vorhanden sind
if ~isempty(lines)
% die Linie ermitteln, die am nächsten zum Fahrzeug liegt. Diese
% ist die gesuchte Stopplinie.
lines_rho = [lines(:,:).rho];
[rho_nearest_line, index_nearest_line] = max(lines_rho);
stoppline = lines(index_nearest_line);
Für eine spätere Bestimmung des Abstands der Stopplinie zum Fahrzeug durch eine Koordinatentransformation wird der Mittelpunkt der Linie berechnet.
% Mittelpunkt der Linie aus Startpunkt und Endpunkt berechen
xy_center = stoppline.point1+(stoppline.point2-stoppline.point1)./2
Visualisierung der gefundenen Stopplinie
Für die Darstellung der detektierten Stopplinie wird diese zum einen in den Graustufenbildausschnitt und zum anderen in das ursprüngliche Originalbild eingezeichnet. Dabei wird die Linie und rot dargestellt, der Startpunkt gelb, der Endpunkt rot sowie der Linienmittelpunkt grün dargestellt. Bei der Visualisierung im Originalbild ist zu beachten, dass die Koordinatenverschiebung der Linie durch die Beschränkung auf einen Bildausschnitt mit eingerechnet wird.
%% Visualisierung in ROI-Bild
% Plot Startpunkt und Endpunkt der Stopplinie
xy = [stoppline.point1; stoppline.point2];
plot(xy(1,1),xy(1,2),'x','LineWidth',2,'Color','yellow');
plot(xy(2,1),xy(2,2),'x','LineWidth',2,'Color','red');
% Plot Mittelpunkt der Linie
plot(xy_center(1,1),xy_center(1,2),'x','LineWidth',2,'Color','green');
% Plot Stopplinie
plot(xy(:,1),xy(:,2),'LineWidth',2,'Color','red');
%% Visualisierung in Originalbild
% Umrechnung der Koordinaten des ROI-Bilds in das ursprüngliche
% Originalbild
xy_center_inputimage = zeros(1,2);
xy_center_inputimage(1,1) = xy_center(1,1)+roi(1,1);
xy_center_inputimage(1,2) = xy_center(1,2)+roi(1,2);
stoppline_inputimage = stoppline;
stoppline_inputimage.point1(1,1) = stoppline_inputimage.point1(1,1)+roi(1,1);
stoppline_inputimage.point1(1,2) = stoppline_inputimage.point1(1,2)+roi(1,2);
stoppline_inputimage.point2(1,1) = stoppline_inputimage.point2(1,1)+roi(1,1);
stoppline_inputimage.point2(1,2) = stoppline_inputimage.point2(1,2)+roi(1,2);
% Plot Startpunkt und Endpunkt der Stopplinie
subplot(1,3,1), hold on
xy_inputimage = [stoppline_inputimage.point1; stoppline_inputimage.point2];
plot(xy_inputimage(1,1),xy_inputimage(1,2),'x','LineWidth',2,'Color','yellow');
plot(xy_inputimage(2,1),xy_inputimage(2,2),'x','LineWidth',2,'Color','red');
% Plot Mittelpunkt der Linie
plot(xy_center_inputimage(1,1),xy_center_inputimage(1,2),'x','LineWidth',2,'Color','green');
% Plot Stopplinie
plot(xy_inputimage(:,1),xy_inputimage(:,2),'LineWidth',2,'Color','red');
end
pause(0.000001)
end
Laufzeit
Die Laufzeit des beschriebenen Algorithmus wird in dem folgenden Diagramm dargestellt.
BILD
Es ergibt sich eine Gesamtlaufzeit von 0,00779 Sekunden pro Frame.
Optimierung
Der beschrieben Algorithmus erfüllt alle Anforderungen der Aufgabenstellung. Um die Robustheit des Algorithmus jedoch noch weiter zu erhöhen wäre es möglich noch weitere Merkmale einer Stopplinie zur Detektion hinzu zu ziehen. Ein sich besonders anbietendes Merkmal ist die Tatsache, dass eine Stopplinie stets orthogonal zur rechten Markierung des Fahrbahnrandes verläuft. Daher besteht die Möglichkeit diese Markierung ebenfalls durch eine Hough-Transformation zu detektieren. Durch die Berechnung des Schnittwinkels, beziehungsweise des Skalarprodukts, der Geraden in Vektorform kann eine Aussage über die Orthogonalität der Linien getroffen werden. Das Ergebnis dieser Berechnung liegt für eine sich mit der Markrierung des Fahrbahnrands rechtwinkelig schneidende Stopplinie in einem Bereich von etwa im Falle des Schnittwinkels oder aber bei ungefähr Null für das Skalarprodukt.
YouTube-Video
Dieses YouTube-Video zeigt die Fahrt auf einer Rundstrecke, bei der die Stopplinien erkannt werden. Die Startlinie zum Ende des Videos wird, wie gefordert, nicht als Stopplinie interpretiert.
Einzelnachweise
- ↑ MathWorks Documentation: hough Website der MathWorks Dokumentation zur Hough-Transformation. Abgerufen am 30. Juni 2018.
- ↑ MathWorks Documentation: houghpeaks Website der MathWorks Dokumentation zur Identifikation von Spitzen einer Hough-Transformation. Abgerufen am 30. Juni 2018.
- ↑ MathWorks Documentation: houghlines Website der MathWorks Dokumentation zum Ermitteln con Liniensegmenten auf Basis einer Hough-Transformation. Abgerufen am 30. Juni 2018.
Weblinks
BSD-Lizenzbedingung BSD-Lizenz
Copyright (c) 2014, Hochschule Hamm-Lippstadt, Dep. Lip. 1, Prof. Schneider
Hochschule Hamm-Lippstadt. Alle Rechte vorbehalten.
→ zurück zum Hauptartikel: Digitale Signal- und Bildverarbeitung SoSe2018