Ballbalancierer: Unterschied zwischen den Versionen

Version vom 21. Januar 2014, 18:45 Uhr

Einführung

Der Ballbalancierer ist ein Laborversuch an dem das Verhalten verschiedener Reglertypen untersucht und erlernt werden kann. Dabei wird ein Ball auf einer Wippe balanciert. Diese wird hierbei von einem Servomotor abhängig von der aktuellen Postion des Balles in Schieflage gebracht, wodurch der Ball durch die Erdanziehungskraft beschleunigt wird und beginnt zu rollen. An welche Sollposition auf der Wippe der Ball bei diesem Versuch gebracht werden soll, ist frei einstellbar. Außerdem kann das Verhalten von PID-Reglern an diesem Aufbau erforscht werden, da auch die Gewichtung der einzelnen Regelanteile steuerbar ist.

Versuchsaufabu

Mechanischer Aufbau

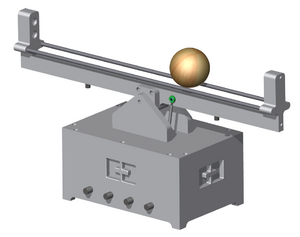
Der mechanische Aufbau des Ballbalancierers, der in Abbildung 1 zu sehen ist, lässt sich in zwei Bereiche unterteilen. Er besteht aus einem Gehäuse und einer darauf montierten Wippe. Das Gehäuse dient als Stauraum für den Servomotor und Teile der Elektronik. Beim Servomotor handelt es sich um einen "Multiplex Rhino pro SHV digi 4" mit einem maximalen Stellmoment von 230 N/cm bei 6V Betriebsspannung. Allerdings kann der Ballbalancierer davon lediglich 192 N/cm nutzen, weil er nur mit 5V betrieben wird. Das ist aber immer noch mehr als genug, um den Wippenarm bewegen zu können selbst wenn der Ball an einem Ende Wippe liegt und so das Moment maximal wird. In der Wippe selbst sind zwei Rillenkugellager verbaut, die dafür sorgen, dass die Wippe den Winkeländerungen durch den Servomotor auch folgen kann. Außerdem besitzt sie einseitig eine Vorrichtung um einen Sensor aufnehmen zu können. Für jeden vorhandenen Sensor existiert dabei ein passendes Gehäuse, sodass diese einfach austauschbar sind. Außerdem sind zwei unterschiedliche Bälle vorhanden. Die Abmessungen dieser sind identisch, der Unterschied besteht lediglich im Material und folglich im Gewicht. Einer der Bälle ist aus Holz, der andere aus Styropor.

Elektrotechnischer Aufbau

Der Ballbalancierer verfügt über drei verschiedene Baugruppen, die elektronisch steuerbar sind.

- 3 LED          : Dienen zum Anzeigen verschiedener Status wie z.B., dass das Gerät eingeschaltet ist oder der Ball sich aktuell in Sollposition befindet
- 4 Potentiometer: Jeweils 1, um die Gewichtung eines Teils des PID-Reglers zu steuern und 1 um die Sollposition des Balles festzulegen
- 1 Servomotor   : Setzt die Befehle des Reglers in Stellwinkel um und balanciert so den Ball in Sollposition.

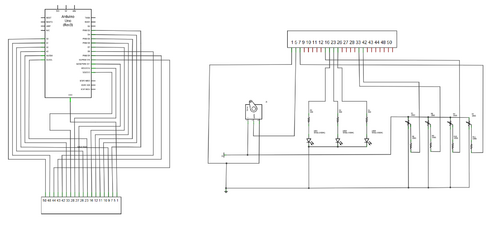
Der Ballbalancierer verfügt zudem noch über zwei Sensoren mit denen die Position des Balles auf der Wippe bestimmt werden kann. Es handelt sich um einen Ultraschallsensor und einen Infrarotsensor, von denen immer nur einer verwendet werden kann. Außerdem besitzt der Ballbalancierer einen 50-poligen Stecker. Die einzelnen Bauelemente belegen dabei wie in Abbildung 2 zu sehen ist die entsprechenden Pins. Über diesen Stecker ist der Ballbalancierer mit einem Arduino Uno verbunden. Dieser steuert den Ballbalancierer gemäß dem auf ihm gespeicherten Regler. Zur Entwicklung oder Verbesserung von Regelungsalgorithmen eine Programmierung mit Matlab Simulink oder der Arduino Entwicklungsumgebung zu empfehlen.

Wichtige Größen des Systems

Um einen Regler für das System entwickeln zu können ist wichtig zu wissen welche Größen das System charakterisieren. Erst dadurch kann erreicht werden, dass sich das entwickelte Modell physikalisch so verhält wie die Realität. Verwendet man die Holzkugel sind folgende Werte von Bedeutung:

- m = 0,124kg      : Gewicht der Kugel (Holz)
- r = 0,04m        : Radius der Kugel
- g = 9,81m/s²     : Erdbeschleunigung
- L = 0,6m         : Länge der Regelstrecke bzw. des Wippenarms
- d = 0,009        : Hebelarm des Servomotors
- J = 0,000128kg*m²: Massenträgheitsmoment der Kugel
- c = 0,06m        : Abstand zwischen Aufhängung und Servobefestigung

Theoretische Lösung

veränderliche Größen und wirkende Kräfte

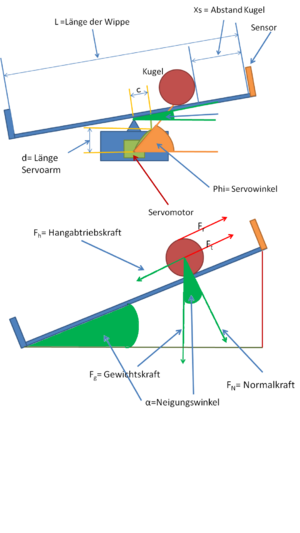
Es gibt nur eine Größe, den Sensorwinkel Φ die , wenn der Austausch der Kugel außer acht gelassen wird, im System änderbar ist. Diese hat direkten Einfluss auf den Neigungswinkel α. $alpha = (d/c)*phi$ Die Hangabtriebskraft F_h und die Summe aus der Rotationskraft F_r $Fr=(J/(r)^2)*a$ und der Translationskraft F_t $Ft=m*a$ (vgl.Abb.3) bilden nach dem 2. Newtonsche Gesetz ein Kräftegleichgewicht. $Fr+Ft=Fh$ daraus ergibt sich folgende Formel $(J/(r)^2)*a+m*a=m*g*sin(alpha)$ beachtet man das Trägheitsmoment der Kugel $J=(2/5)*m*r^2$ ergibt sich $(2/5)*m*a+m*a=m*g*sin(alpha)$ für a folgt daraus $a = (5/7)*g*sin(alpha)$ für kleine Winkel von α kann folgendes angenommen werden $sin(alpha)=alpha$ und daraus folgend $a= (5/7*g*alpha)$ . Durch diese Formel ist das Bewegungsmodell des Balles beschrieben. Für die Übertragungsfunktion mit $a = (d^2*s)/(d*t^2)$ ergibt sich nach der Laplace Transformation $(X(S)/alpha(S))=(((5/7)*g)S^2)$ .

Regelkreis

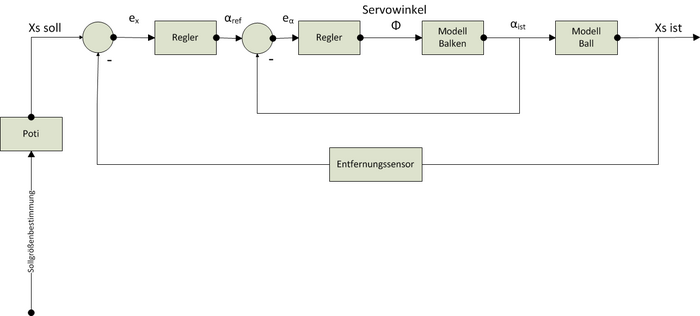
Das System des Ballbalancierer lässt sich durch einen geschachtelten Regelkreis darstellen. Als Eingangsgröße wird der Abstand der Kugel zum Snesor gewählt (Xs_soll) dieser lässt sich über einen Poti beliebig einstellen. Die Ausgangsgröße ist der aktuelle Abstand (Xs_ist). Dieser wird über den Entfernungssensor gemessen und zurückgeführt. Ex ist die Differenz aus Xs_soll und Xs_ist. Aus dieser Differenz wird ein Referenzwert α_ref für den Neigungswinkel α des Balkens berechnet. Die Differenz aus diesem und dem α_ist ergibt den einzustellenden Neigungswinkel. Im inneren Regelkreis wird dieser in den zu stellenden Servowinkel umgerechnet. Über den Servo wird dieser Winkel eingestellt und der Balken neigt sich durch die auf die Kugel wirkende Hangantriebskraft beginnt diese zu rollen.

Regelungstechnische Herausforderungen

Mechanische Herausforderungen

Kugel

Eine Herausforderung bestand darin mit den gegebenen geometrischen Eigenschaften der Kugel zurecht zu kommen. Diese sind Ursache für ein sensortechnisches Problem. Um dies zu erläutern ist es wichtig die Funktionsweise eines Ultraschallsensors verstanden zu haben. Ein Ultraschallsensor besteht aus einem Sender und einem Empänger. Beide verfügen über eine Membran, die zum Schwingen angeregt werden kann. Möchte man eine Messung durchführen, so regt man die Membran die Membran des Senders dazu an in einer bestimmten Frequenz zu schwingen. Dabei entstehen Wellen, die sich abhängig von der Bauform des Sensors kegelförmig im Raum ausbreiten. Treffen sie dabei auf ein Objekt, werden sie von diesem reflektiert und treffen auf ihrem Rückweg auf den Ultraschallempfänger. Dessen Membran beginnt dabei ebenfalls zu schwingen was erfasst und in ein eletrisches Signal umgewandelt wird. Über die Zeitdifferenz zwischen dem Aussenden der Schallwellen und dem Moment des Wiederauftreffens auf die Empfängermembran kann bei bekannter Schallgeschwindigkeit auf den Abstand zum Objekt geschlossen werden von dem die Schallwellen reflektiert wurden. Schwierig wird dieser Vorgang wenn die zu detektierenden Objekte sehr klein sind, was auf den ersten Blick bei der verwendeten Kugel nicht der Fall ist. Immerhin hat diese einen Radius von 4cm. Aber auch für Ultraschallwellen gilt das Reflexionsgesetz also Einfallswinkel gleich Ausfallswinkel. Um wieder zum Ultraschallsensor zurückzukehren müssen die Wellen beinahe senkrecht auf das Objekt treffen. Im Fall einer Kugel ist also die Fläche, die die Wellen so reflektiert, dass sie detektiert werden können, sehr klein. Genau betrachtet ist eine Kugel sogar der Körper, der für die Erfassung mittels Ultraschall am schlechtesten geeignet ist. Die Auswirkung dieser Schwierigkeit sind sehr stark verrauschte Messwerte.

Lego - Wagen

Da die Kugel wie oben beschrieben nur schlecht für die Erfassung durch einen Ultraschallsensor geeignet ist, liegt Idee nahe diese einfach durch etwas anderes zu ersetzen. Baut man beispielsweise aus Lego einen Wagen, der in der Mitte eine ebene Fläche besitzt, die senkrecht zu den ausgesendeten Ultraschallwellen verläuft, kann man das Problem mit der Kugelgeometrie umgehen. Abbildung ??? zeigt ein Beispiel für einen solchen Wagen. Allerdings weist auch dieser Schwachstellen auf. Eine davon besteht darin, dass der Wagen natürlich nicht gleichen Eigenschaften besitzt wie die Kugel. Die unter "Wichtige Größen des Systems" aufgeführten Größen sind teilweise auf den Wagen gar nicht anwendbar wie z.B. der Radius oder deutlich schwieriger zu bestimmen wie z.B. das Massenträgheitsmoment. Der unter "Theoretische Lösung" aufgezeigte Ansatz für einen PID-Regler ist also auf einen Wagen so gar nicht anzuwenden. Es müsste ein neuer Regler für den Wagen ausgelegt werden. Außerdem hat der Wagen noch weitere mechanische Schwachstellen. Er rollt deutlich schlechter als die Kugel auf den Schienen, sodass es mitunter passieren kann, dass er sich verkantet und sich ohne Eingriff von außen gar nicht mehr bewegt. Es besteht auch die Möglichkeit, dass der Wagen von den Schienen herunterfällt, wenn der Servomotor, aufgrund einer großen Regeldifferenz, einen großen Weg fährt, während der Wagen sich fast an einem Ende des Wippenarm befindet.

Austauschbarkeit von Sensoren

Aufgrund der erläuterten Schwierigkeiten mit dem verbauten Ultraschallsensor bzw. Kugel wäre eine schnelle Austauschbarkeit der Komponienten wünschenswert. Insbesondere weil dem Ballbalancierer ein Infrarotsensor beiliegt, der bei der Erkennung des Balles deutlicht besser funktioniert als der Ultraschallsensor, der wie beschrieben eher für den Lego-Wagen eingesetzt werden kann. Der Sensor ist direkt mit dem 50-poligen Stecker verbunden, sodass eine Austausch nur möglich ist, wenn der Ballbalancierer weitgehend auseinandergebaut wird.

Sensortechnische Herausforderungen

Ultraschallsensor

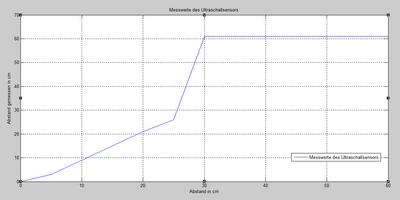
Der Ultraschallsensor weist nicht nur, wie bereits erläutert, Probleme mit dem Erkennen eines Balles auf, sondern sorgt auch überdies hinaus für Schwierigkeiten. Laut Datenblatt ist der Ultraschallsensor in der Lage Objekte bis zu einer entferung von 3m zu erkennen. Dabei funktioniert er auf kurze Distanz besser als auf lange Entfernungen. Dem Datenblatt zufolge erstreckt sich dieser Bereich in dem der Sensor gut funktioniert über die ersten 30cm, bei größeren Abständen nimmt das Messrauschen stark zu. Dieses Verhalten wird durch Abbildung ??? bestätigt. Dabei wurde der wahre Abstand zum Objekt in Schritten von jeweils 5cm erhöht und gegen die Messwerte des Sensors dargestellt. Hierbei ist zu erwähnen, dass in der Grafik oft der Wert 61cm angegeben ist, was leicht über der gesamten Länge des Wippenarms liegt. In diesen Fällen lieferte der Sensor überhaupt kein konstantes Ergebnis. Es wurden dabei teilweise Messwerte von über 30m vom ausgegeben.

Auswirkungen dieses Problems war, dass auf der zweiten Hälfte des Wippenarms kaum eine Regelung möglich war.

Infrarotsensor

Der Infrarotsensor stellt eine Alternative zum Ultraschallsensor dar und weist nicht die beschriebenen Schwierigkeiten auf. Allerdings zeigt auch dieser Schwächen bei der Bewältigung der Aufgabe. Im Gegensatz zum Ultraschallsensor liegt sein Schwachpunkt in sehr kurzen Abständen zum zu erkennenden Objekt. Laut Datenblatt besitzt er eine Totfläche von 10cm, was immerhin schon einem Sechstel der gesamten Wippenarmlänge entspricht. Dies konnte durch Test bestätigt werden. Rollt der einmal in diesen Bereich hinein oder lässt man ihn dort starten, kann nicht normal nach dem Regelalgorithmus des PID-Reglers verfahren werden. Besonders Problematisch wird dies wenn die über das Potentiometer gewählte Sollposition der Kugel in diesem Bereich liegt.

Fazit

Ein Projektabschluss ist aufgrund der beschriebenen Probleme bisher noch nicht erfolgt. Allerdings existieren Lösungsansätze um die aufgetretenen Herausforderungen zu bewältigen. Das Problem mit den Sensoren ließe sich möglicherweise bereits lösen, wenn ein Ultraschall bzw. Infrarotsensor genutzt wird der besser für den Bereich 0cm - 60cm geeignet ist als die bisher vorhandenen. Denkbar wäre aber auch auf eine andere Technologie zur Entferungsmessung zu setzen. Die Laserentferungsmessung würde sich anbieten. Alternativ wäre es auch möglich eine Kugel mit elektrisch leitender Oberfläche zu verwenden und eine Spannung an die Schienen, auf denen sie sich bewegt, anzulegen. Misst man dann den Widerstand kann auf die Position der Kugel geschlossen werden. Der Ballbalancierer ist nun mit einem Stecker versehen durch den der Austausch der Sensoren schnell und einfach möglich ist ohne ihn weitesgehend auseinanderbauen zu müssen. Es wäre somit wohl leichter das Problem der Entfernungsmessung durch einen passenderen Sensor zu lösen als auf alternative Objekte wie z.B. den Wagen zu setzen, da in diesem Fall kein komplett neuer Regler auslegt werden müsste.

@@ Zeile 38: / Zeile 38: @@
 Es gibt nur eine Größe, den Sensorwinkel Φ die , wenn der Austausch der Kugel außer acht gelassen wird, im System änderbar ist.
 Diese hat direkten Einfluss auf den Neigungswinkel α. <math>alpha = (d/c)*phi</math>
-Die Hangabtriebskraft F<sub>h</sub> und die Summe aus der Rotationskraft F<sub>r</sub> <math>Fr=(J/(r)^2)*a </math>  und der Translationskraft F<sub>t</sub> <math>Ft=m*a</math> (vgl.Abb.3) bilden  nach dem 2. Newtonsche Gesetze ein Kräftegleichgewicht.
+Die Hangabtriebskraft F<sub>h</sub> und die Summe aus der Rotationskraft F<sub>r</sub> <math>Fr=(J/(r)^2)*a </math>  und der Translationskraft F<sub>t</sub> <math>Ft=m*a</math> (vgl.Abb.3) bilden  nach dem 2. Newtonsche Gesetz ein Kräftegleichgewicht.
 <math>Fr+Ft=Fh</math> daraus ergibt sich folgende Formel  <math>(J/(r)^2)*a+m*a=m*g*sin(alpha)</math> beachtet man das Trägheitsmoment der Kugel  <math>J=(2/5)*m*r^2</math> ergibt sich <math>(2/5)*m*a+m*a=m*g*sin(alpha)</math>
 für a folgt daraus <math>a = (5/7)*g*sin(alpha)</math> für kleine Winkel von α kann folgendes angenommen werden <math>sin(alpha)=alpha</math> und daraus folgend <math>a= (5/7*g*alpha)</math> . Durch diese Formel ist das Bewegungsmodell des Balles beschrieben. Für die Übertragungsfunktion mit <math>a = (d^2*s)/(d*t^2)</math> ergibt sich nach der Laplace Transformation <math>(X(S)/alpha(S))=(((5/7)*g)S^2)</math>.