Objekterkennung mit LiDAR-Sensor: Unterschied zwischen den Versionen
| (43 dazwischenliegende Versionen von 3 Benutzern werden nicht angezeigt) | |||
| Zeile 4: | Zeile 4: | ||
→ zurück zum übergeordneten Artikel: [[Systemarchitektur|Systemarchitektur]]<br/> | → zurück zum übergeordneten Artikel: [[Systemarchitektur|Systemarchitektur]]<br/> | ||
=Einleitung= | |||
In diesem Artikel wird auf die Auswertung von LiDAR-Messdaten eingegangen. Es wird beschrieben, wie die Messdaten umgewandelt werden können, sodass diese in Matlab verwendet und dargestellt werden können. Des Weiteren werden die Spezifikationen das Datenblatts mit der Testmessung vergleicht. Abschließend wird beschrieben, wie eine Auswertung der Messdaten mit Hilfe von Segmentierung erfolgen kann. | |||
=Auswertung der Messdaten= | =Auswertung der Messdaten= | ||
Nachfolgend wird die Auswertung der Messdaten genauer beschrieben. Zunächst wird der Begriff der LiDAR Daten genauer erläutert. Es folgt die Beschreibung der Lade- und Darstellungsfunktion sowie des zyklischen Ladens der Messdaten. Zuletzt wird auf die Spezifikationsübersicht des URG-04LX eingegangen. | |||
==LiDAR Daten== | ==LiDAR Daten== | ||
Der Begriff LiDAR | Der Begriff LiDAR setzt sich aus „Light Detection And Ranging“ zusammen. Dabei nutzt der LiDAR einen rotierenden Laser über den die Entfernungen gemessen werden. | ||
In Abbildung 1 ist eine beispielhafte Visualisierung des Sensorbilds zu erkennen. | In Abbildung 1 ist eine beispielhafte Visualisierung des Sensorbilds zu erkennen. Besonders gut erkennbar sind hier die jeweiligen Distanzen, die bei einem Umlauf gemessen wurden. Der hier verwendete Sensor hat einen Messbereich von 240°. In diesem Umkreis kann so die Lage von etwaigen Hindernissen bestimmt werden. | ||
[[Datei:UrgBenriVisualisierungssoftware.png|600px|thumb|left|Abbildung 1: UrgBenri Visualisierungssoftware]] | [[Datei:UrgBenriVisualisierungssoftware.png|600px|thumb|left|Abbildung 1: UrgBenri Visualisierungssoftware]] | ||
<br><br><br><br><br><br><br><br><br><br><br><br><br><br><br><br><br><br><br><br> | |||
==Laden der Messdaten== | ==Laden der Messdaten== | ||
| Zeile 86: | Zeile 89: | ||
== Darstellung der Messdaten == | == Darstellung der Messdaten == | ||
Über das Skript startDarstellungDerMessdaten.m können die Messdaten dargestellt werden. In Abbildung 2 | Über das Skript startDarstellungDerMessdaten.m können die Messdaten dargestellt werden. In Abbildung 2 ist eine beispielshafte Darstellung von Messdaten abgebildet. | ||
[[Datei:DarstellunMessdatenLiDAR.png|400px|thumb|left|Abbildung 2: Darstellung der Messdaten]] | [[Datei:DarstellunMessdatenLiDAR.png|400px|thumb|left|Abbildung 2: Darstellung der Messdaten]] | ||
| Zeile 104: | Zeile 107: | ||
Mit dem Skript testeLadeMessdaten.m lässt sich die Funktion testen: | Mit dem Skript testeLadeMessdaten.m lässt sich die Funktion testen: | ||
%% MALTAB initisalisieren | %% MALTAB initisalisieren | ||
| Zeile 190: | Zeile 192: | ||
= Bewertung der Messwerte= | = Bewertung der Messwerte= | ||
Um die aus den LiDAR-Daten | Um die aus den LiDAR-Daten ausgewerteten Daten mit den im Datenblatt angegebenen Werten zu vergleichen, wurden die spezifischen Messwerte berechnet. Die folgende Tabelle zeigt die jeweiligen Werte im Vergleich. | ||
<br> | <br> | ||
| Zeile 219: | Zeile 221: | ||
|} | |} | ||
Wie zu erkennen, passen die in der Theorie angegebenen Werte mit den in der Praxis gemessenen | Wie zu erkennen, passen die in der Theorie angegebenen Werte mit den in der Praxis gemessenen Werten überein. | ||
<br> | |||
Für die Bewertung der Messunsicherheit wurde eine Reihe von Messdaten ausgewertet, die aufgenommen wurden, während sich ein reales Objekt mit bekannter Breite bewegt. Dafür wurden die Messungen als einzelne Frames dargestellt und aneinandergereiht, um anschließend die vom LiDAR gemessene Breite des Objektes bei unterschiedlichen Entfernungen abzulesen. | |||
Die Ergebnisse werden folgend tabellarisch dargestellt. | |||
<br> | |||
{| class="mw-datatable" style="text-align:center" | |||
! style="font-weight: bold;" | Entfernung [m] | |||
! style="font-weight: bold;" | Objektbreite [mm] | |||
! style="font-weight: bold;" | Gemessene Breite [mm] | |||
! style="font-weight: bold;" | Messunsicherheit [mm] | |||
! style="font-weight: bold;" | Angegebene Genauigkeit [mm] | |||
|- | |||
| 0,2 | |||
| 134 | |||
| 132 | |||
| 2 | |||
| +/- 30 | |||
|- | |||
| 1 | |||
| 134 | |||
| 122 | |||
| 12 | |||
| +/- 30 | |||
|- | |||
| 2 | |||
| 134 | |||
| 103 | |||
| 31 | |||
| +/- 60 | |||
|- | |||
| 3 | |||
| 134 | |||
| 93 | |||
| 41 | |||
| +/- 90 | |||
|- | |||
| 4 | |||
| 134 | |||
| 96 | |||
| 38 | |||
| +/- 120 | |||
|} | |||
Somit sind auch die vom Hersteller angegebenen Genauigkeiten eingehalten. | |||
= Abstand der Messwerte = | = Abstand der Messwerte = | ||
Ein Kriterium, ob ein Punkt zu einem Segment zugeordnet werden darf, ist der Abstand zu anderen Messpunkten. Je weiter der LiDAR-Sensor von einem Objekt entfernt ist, desto weiter können | Ein Kriterium, ob ein Punkt zu einem Segment zugeordnet werden darf, ist der Abstand zu anderen Messpunkten. Je weiter der LiDAR-Sensor von einem Objekt entfernt ist, desto weiter können die Messpunkte auseinander liegen, welche zu einem Objekt zugeordnet werden dürfen. Wie groß die minimale Entfernung zwischen zwei Messpunkten ist, hängt von der Winkelauflösung des Sensors ab sowie von der Entfernung des Sensors zu den jeweiligen Messpunkten. | ||
Mithilfe des Skripts "berechneMinimalAbstand.m" und der inneliegenden Funktion "minAbstand" kann diese minimale Entfernung berechnet werden: | Mithilfe des Skripts "berechneMinimalAbstand.m" und der inneliegenden Funktion "minAbstand" kann diese minimale Entfernung berechnet werden: | ||
| Zeile 246: | Zeile 294: | ||
end | end | ||
Die Abbildung 3 zeigt die lineare Abhängigkeit des minimalen Abstands von der Entfernung des Sensors zu den Messpunkten. | |||
[[Datei:HokuyoLidar_MinimalerAbstandzwischenMesspunkten.png|600px|thumb|left|Abbildung 3: Minimaler Abstand zwischen Messpunkten]] | [[Datei:HokuyoLidar_MinimalerAbstandzwischenMesspunkten.png|600px|thumb|left|Abbildung 3: Minimaler Abstand zwischen Messpunkten]] | ||
<br><br><br><br><br><br><br><br><br><br><br><br><br><br><br><br> | <br><br><br><br><br><br><br><br><br><br><br><br><br><br><br><br> | ||
= Segmentierung = | = Segmentierung = | ||
Eine weitere Aufgabe, die typisch für die Auswertung von LiDAR Messdaten ist, ist die Segmentierung. Dabei werden unterschiedliche Algorithmen verwendet. Wir haben uns im Praktikum mit dem sogenannten Succesive Edge Following beschäftigt. | |||
Dabei konnten wir auf eine fertige Funktion zurückgreifen, die aus den RangeScan Messwerten Segmentierungen bildet und diese in einem Struct mit vielen weiteren Daten ablegt. <br> | Dabei konnten wir auf eine fertige Funktion zurückgreifen, die aus den RangeScan Messwerten Segmentierungen bildet und diese in einem Struct mit vielen weiteren Daten ablegt. <br> | ||
Das Struct, das der SuccesiveEdgeFollowing Algorithmus zurückgibt besteht aus der Objekt ID | Das Struct, das der SuccesiveEdgeFollowing Algorithmus zurückgibt, besteht aus der Objekt ID sowie den linken, den nächsten und den rechten Punkt des Segments. Zusätzlich werden diese Punkte in Polar- und Kartesischen Koordinaten angegeben. <br> | ||
Mithilfe des im Folgenden | Mithilfe des im Folgenden dargestellten Codes konnte das Objekt aus der Funktion gelesen werden und es werden die 3 Punkte aus der Funktion miteinander verbunden. Dies dient im Wesentlichen zur Datenreduktion, da so anstatt zahlreicher Punkte des LiDARs nur noch 3 Punkte pro Segment ausgewertet werden müssen. | ||
segment=SucessiveEdgeFollowing(RangeScan(1,:)); | segment=SucessiveEdgeFollowing(RangeScan(1,:)); | ||
| Zeile 270: | Zeile 316: | ||
end | end | ||
Die Abbildung 4 zeigt, dass bei kleineren Objekten die Reduktion auf die 3 Punkte gut funktioniert. Jedoch kommt diese Vereinfachung bei großen und anders gedrehten Objekten, wie dem auf der linken Seite, an seine Grenzen, sodass dort die blaue Linie nicht ganz zum Objekt passt. | |||
[[Datei:Segmentierung SuccessiveEdgeFollowing.png |500px|thumb|left|Abbildung 4: Segmentierung mit dem Succesive Edge Following Algorithmus]] | |||
<br><br><br><br><br><br><br><br><br><br><br><br><br><br><br><br><br><br><br><br> | |||
Die Funktion und das kurze | Die Funktion und das kurze Auswertungsscript liegen unter folgendem Pfad: https://svn.hshl.de/svn/MTR_SDE_Praktikum/trunk/Workshops/Abgaben/Teamabgaben/Workshop10 <br> | ||
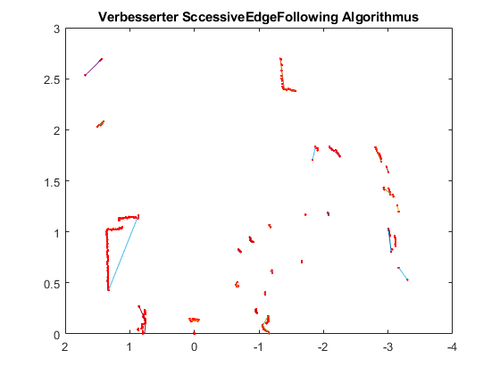
Mithilfe der oben erläuterten Funktion des kleinsten Abstands konnte der Successive | Mithilfe der oben erläuterten Funktion des kleinsten Abstands konnte der Successive Edge Following Algorithmus verbessert werden, sodass weniger Segmente gefunden werden, da der Suchwinkel mit größer werdendem X ebenfalls größer wird. In der folgenden Abbildung 5 ist das verbesserte Segmentierungsergebnis zu sehen. | ||
[[Datei:Vebresserung_Segmentierung_SuccessiveEdgeFollowing.png |500px|thumb|left|Abbildung | [[Datei:Vebresserung_Segmentierung_SuccessiveEdgeFollowing.png |500px|thumb|left|Abbildung 5: Verbesserte Segmentierung mit dem Succesive Edge Following Algorithmus]] | ||
Aktuelle Version vom 13. Juli 2021, 14:11 Uhr
Autor: SDE Team 2021/2022
Betreuer: Ulrich Schneider
→ zurück zum übergeordneten Artikel: Systemarchitektur
Einleitung
In diesem Artikel wird auf die Auswertung von LiDAR-Messdaten eingegangen. Es wird beschrieben, wie die Messdaten umgewandelt werden können, sodass diese in Matlab verwendet und dargestellt werden können. Des Weiteren werden die Spezifikationen das Datenblatts mit der Testmessung vergleicht. Abschließend wird beschrieben, wie eine Auswertung der Messdaten mit Hilfe von Segmentierung erfolgen kann.
Auswertung der Messdaten
Nachfolgend wird die Auswertung der Messdaten genauer beschrieben. Zunächst wird der Begriff der LiDAR Daten genauer erläutert. Es folgt die Beschreibung der Lade- und Darstellungsfunktion sowie des zyklischen Ladens der Messdaten. Zuletzt wird auf die Spezifikationsübersicht des URG-04LX eingegangen.
LiDAR Daten
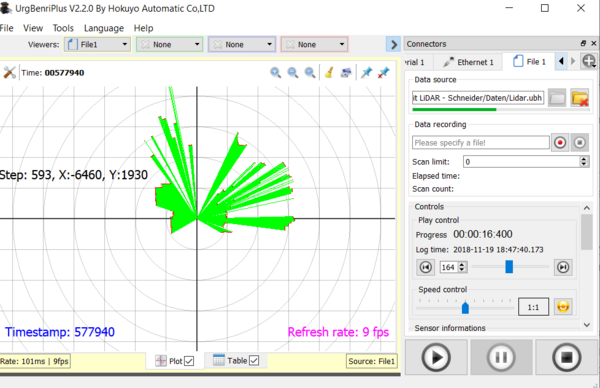
Der Begriff LiDAR setzt sich aus „Light Detection And Ranging“ zusammen. Dabei nutzt der LiDAR einen rotierenden Laser über den die Entfernungen gemessen werden. In Abbildung 1 ist eine beispielhafte Visualisierung des Sensorbilds zu erkennen. Besonders gut erkennbar sind hier die jeweiligen Distanzen, die bei einem Umlauf gemessen wurden. Der hier verwendete Sensor hat einen Messbereich von 240°. In diesem Umkreis kann so die Lage von etwaigen Hindernissen bestimmt werden.
Laden der Messdaten
Mit dem Code der Datei startUBH2MAT.m werden die Messdaten geladen und in einer .mat-Datei gespeichert.
%**************************************************************** % Modul : startUBH2MAT.m * % * % Datum : 24. Juni 2021 * % * % Funktion : Messdaten der Dateien LiDAR.ubh laden und * % verarbeiten * % * % * % * % * % Implementation : MATLAB R2020a * % * % Author : SDE-Team 20/21 * % * % Bemerkung : - * % * % * % Letzte Änderung : 29. Juni 2021 * % * %****************************************************************
%% MALTAB initisalisieren
clear all; close all; clc
%% Dateipfad temporär hinzufügen
dateiPfad = ['...\MTR_SDE_Praktikum\trunk\...']
addpath(dateiPfad);
dateiName = 'Lidar.ubh'; % Eingangsdatei
nSamples = 682; % Anzahl der Messwerte
%% Datei öffnen
fileID= fopen(dateiName);
if fileID == -1
error("Datei ist nicht vorhanden");
end
daten={};
%% Winkel berechnen
Aufloesung = (120--120)/(nSamples-1);% Winkelauflösung
aWinkel= -120:Aufloesung:120 ; % [-a:Aufloesung:a];
%% Einmalige Winkelberechnung
acosdw = cosd(aWinkel); % Array mit nSamples Einträgen
asindw = sind(aWinkel); % Array mit nSamples Einträgen
%% Schleife solange die Datei nicht abgearbeitet wurde
% Zeile aus Datei lesen
while ~feof(fileID)
daten=[daten {fgetl(fileID)}];
end
% Zeitstempel in s auslesen
timestamp = daten(32:6:end); %[ms]
timestamp = cellfun(@str2num,timestamp);
Zeit = (timestamp(1,:)-timestamp(1,1))./1000; %[s]
%Log Time
logTime = daten(34:6:end);
%%Schrägentfernungen
range = daten(36:6:end);
range= str2num(char(range));
RangeScan= reshape(range,[682,336])';
% KOS-Trafo Polar- zu kartesische Koordinaten
xMesswerte=asindw.*RangeScan./1000;
yMesswerte=acosdw.*RangeScan./1000;
%% Daten speichern
stSaveFileName = 'Messdaten.mat';
save(stSaveFileName, "Zeit","RangeScan","xMesswerte","yMesswerte");
disp([stSaveFileName,' wurde gespeichert...'])
fclose(fileID);
% .uhb Datei schließen
Darstellung der Messdaten
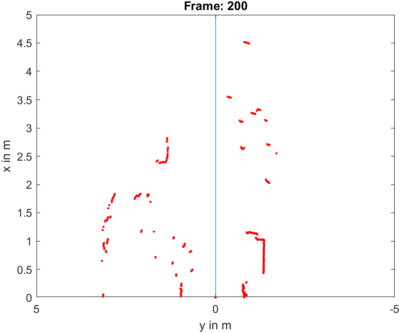
Über das Skript startDarstellungDerMessdaten.m können die Messdaten dargestellt werden. In Abbildung 2 ist eine beispielshafte Darstellung von Messdaten abgebildet.
Zyklisches Laden der Messdaten
Über die Funktion LadeMessdaten.m werden die Messdaten für ein Frame geladen:
function [z,dt,aRangeScan] = LadeMessdaten(i)
% LADEMESSDATEIN läd die Messdaten für ein Frame
Messwerte = load("Messdaten.mat");
dt = Messwerte.Zeit(i);
z = [Messwerte.xMesswerte(i,:); Messwerte.yMesswerte(i,:)];
aRangeScan = Messwerte.RangeScan;
end
Mit dem Skript testeLadeMessdaten.m lässt sich die Funktion testen:
%% MALTAB initisalisieren
clear all; close all; clc
%% Figure vorbereiten
% ROI festlegen
xROI = [-5; 5];
yROI = [0; 5];
fRange = 5.5; % m
figure('units','normalized','outerposition',[0 0 1 1]);
h = plot(0,0,'b.');
%hold on
set(gca,'XDir','reverse');
line([-fRange fRange], [0 0])
line([0 0], [-fRange fRange])
xlabel('y in m');
ylabel('x in m');
ylim manual
xlim manual
hAxis = gca;
hAxis.XLimMode = 'manual';
hAxis.YLimMode = 'manual';
xlim(xROI)
ylim(yROI)
%% Messdaten darstellen
nStart = 1; % Startframe;
nEnde = 336; % Anzahl der Frames
for nFrame=nStart:nEnde % Zyklusschleife über alle Messzyklen
%% Messwerte
[z, dt, aRangeScan] = LadeMessdaten(nFrame);
X = z(1,:);
Y = z(2,:);
set(h, "XData",X );
set(h, "YData", Y);
refreshdata
title(["Frame: ",num2str(nFrame)]);
pause(0.01);
end
Spezifikationsübersicht des URG-04LX
| Name des Produkts | Laser Entfernungsmesser |
|---|---|
| Lichtquelle | Halbleiter Laserdiode (Wellenlänge 785 nm) |
| Versorgungsspannung | 5VDC |
| Maximale Reichweite | 0,002 m bis 5,6 m |
| Messbereich | 0,006 m bis 4 m |
| Messauflösung | 0,001 m |
| Genauigkeit (20mm - 1000mm) | ± 0,03 m |
| Genauigkeit (1000mm - 4000mm) | ± 3 % |
| Horizontaler Scanwinkel | 240° |
| Winkelauflösung | 0,36° |
| Anzahl Scanschritte | 683 |
| Scangeschwindigkeit | 100 ms/scan |
| Schnittstelle | RS-232 (seriell) |
Bewertung der Messwerte
Um die aus den LiDAR-Daten ausgewerteten Daten mit den im Datenblatt angegebenen Werten zu vergleichen, wurden die spezifischen Messwerte berechnet. Die folgende Tabelle zeigt die jeweiligen Werte im Vergleich.
| Name | Datenblatt | berechnete Daten |
|---|---|---|
| Maximale Reichweite | 5,6 m | 5,5 m |
| Scangeschwindigkeit | 100 ms/scan | 99,7 ms /scan |
| Horizontaler Scanwinkel | 240° | 240° |
| Winkelauflösung | 0,36° | 0,35° |
Wie zu erkennen, passen die in der Theorie angegebenen Werte mit den in der Praxis gemessenen Werten überein.
Für die Bewertung der Messunsicherheit wurde eine Reihe von Messdaten ausgewertet, die aufgenommen wurden, während sich ein reales Objekt mit bekannter Breite bewegt. Dafür wurden die Messungen als einzelne Frames dargestellt und aneinandergereiht, um anschließend die vom LiDAR gemessene Breite des Objektes bei unterschiedlichen Entfernungen abzulesen.
Die Ergebnisse werden folgend tabellarisch dargestellt.
| Entfernung [m] | Objektbreite [mm] | Gemessene Breite [mm] | Messunsicherheit [mm] | Angegebene Genauigkeit [mm] |
|---|---|---|---|---|
| 0,2 | 134 | 132 | 2 | +/- 30 |
| 1 | 134 | 122 | 12 | +/- 30 |
| 2 | 134 | 103 | 31 | +/- 60 |
| 3 | 134 | 93 | 41 | +/- 90 |
| 4 | 134 | 96 | 38 | +/- 120 |
Somit sind auch die vom Hersteller angegebenen Genauigkeiten eingehalten.
Abstand der Messwerte
Ein Kriterium, ob ein Punkt zu einem Segment zugeordnet werden darf, ist der Abstand zu anderen Messpunkten. Je weiter der LiDAR-Sensor von einem Objekt entfernt ist, desto weiter können die Messpunkte auseinander liegen, welche zu einem Objekt zugeordnet werden dürfen. Wie groß die minimale Entfernung zwischen zwei Messpunkten ist, hängt von der Winkelauflösung des Sensors ab sowie von der Entfernung des Sensors zu den jeweiligen Messpunkten.
Mithilfe des Skripts "berechneMinimalAbstand.m" und der inneliegenden Funktion "minAbstand" kann diese minimale Entfernung berechnet werden:
clear all
close all
clc
alpha = 0.36; % in °
x = (0:0.1:5.6); % Reichweite des Sensors von 0 - 5.6m in 0.1m Abständen
sMin = zeros(length(x), 1);
for k = 1:length(x)
p1 = [x(k), 0];
sMin(k) = minAbstand(p1, alpha); % Anwenden der untenstehenden Funktion. Ergebnis: Array mit Mindestabständen
end
plot(x, sMin);
grid on
title('Minimaler Abstand zwischen zwei Messpunkten')
xlabel('Entfernung Sensor zu Messpunkten in [m]')
ylabel('Minimaler Abstand zwischen Messpunkten in [m]')
function sMin = minAbstand(p1, alpha) % Funktionsdeklaration berechneMinimalAbstand Input: p1, alpha
sMin = tand(alpha) * norm(p1); % Berechnung des Mindestabstands zwischen zwei Messpunkten
end
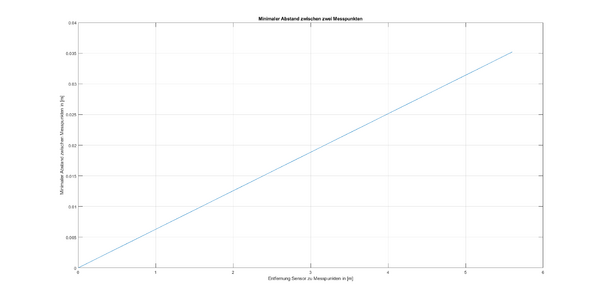
Die Abbildung 3 zeigt die lineare Abhängigkeit des minimalen Abstands von der Entfernung des Sensors zu den Messpunkten.
Segmentierung
Eine weitere Aufgabe, die typisch für die Auswertung von LiDAR Messdaten ist, ist die Segmentierung. Dabei werden unterschiedliche Algorithmen verwendet. Wir haben uns im Praktikum mit dem sogenannten Succesive Edge Following beschäftigt.
Dabei konnten wir auf eine fertige Funktion zurückgreifen, die aus den RangeScan Messwerten Segmentierungen bildet und diese in einem Struct mit vielen weiteren Daten ablegt.
Das Struct, das der SuccesiveEdgeFollowing Algorithmus zurückgibt, besteht aus der Objekt ID sowie den linken, den nächsten und den rechten Punkt des Segments. Zusätzlich werden diese Punkte in Polar- und Kartesischen Koordinaten angegeben.
Mithilfe des im Folgenden dargestellten Codes konnte das Objekt aus der Funktion gelesen werden und es werden die 3 Punkte aus der Funktion miteinander verbunden. Dies dient im Wesentlichen zur Datenreduktion, da so anstatt zahlreicher Punkte des LiDARs nur noch 3 Punkte pro Segment ausgewertet werden müssen.
segment=SucessiveEdgeFollowing(RangeScan(1,:)); plot(xMesswerte(1,:), yMesswerte(1,:),'r.'); hold on for i=1: length(segment) x=[segment(i).LeftCartesian(1) segment(i).NearbyCartesian(1) segment(i).RightCartesian(1)]; y=[segment(i).LeftCartesian(2) segment(i).NearbyCartesian(2) segment(i).RightCartesian(2)]; plot(y,x, '-'); set(gca, 'XDir', 'reverse'); end
Die Abbildung 4 zeigt, dass bei kleineren Objekten die Reduktion auf die 3 Punkte gut funktioniert. Jedoch kommt diese Vereinfachung bei großen und anders gedrehten Objekten, wie dem auf der linken Seite, an seine Grenzen, sodass dort die blaue Linie nicht ganz zum Objekt passt.
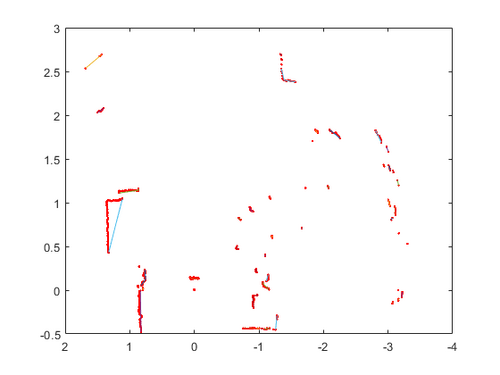
Die Funktion und das kurze Auswertungsscript liegen unter folgendem Pfad: https://svn.hshl.de/svn/MTR_SDE_Praktikum/trunk/Workshops/Abgaben/Teamabgaben/Workshop10
Mithilfe der oben erläuterten Funktion des kleinsten Abstands konnte der Successive Edge Following Algorithmus verbessert werden, sodass weniger Segmente gefunden werden, da der Suchwinkel mit größer werdendem X ebenfalls größer wird. In der folgenden Abbildung 5 ist das verbesserte Segmentierungsergebnis zu sehen.