Halleffektsensor Unipolar (TLE4905L): Unterschied zwischen den Versionen
| (224 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
[[Datei:Infineon TLE4905L.jpg|512px|thumb|rechts|Infinion TLE4905L <ref> https://cdn-reichelt.de/bilder/web/artikel_ws/B400/PICTURE_2SS52M.jpg </ref>]] | [[Datei:Infineon TLE4905L.jpg|512px|thumb|rechts|Infinion TLE4905L <ref> https://cdn-reichelt.de/bilder/web/artikel_ws/B400/PICTURE_2SS52M.jpg </ref>]] | ||
'''Autor:''' [[Benutzer:Mario Wollschlaeger|Mario Wollschläger]] <br/> | '''Autor:''' [[Benutzer:Mario Wollschlaeger|Mario Wollschläger]] <br/> | ||
'''Betreuer:''' [[Benutzer:Ulrich_Schneider|Prof. Dr.-Ing. Ulrich Schneider]]<br/> | '''Betreuer:''' [[Benutzer:Ulrich_Schneider|Prof. Dr.-Ing. Ulrich Schneider]]<br/> | ||
== Einleitung == | == Einleitung == | ||
Dieser Artikel ist im Rahmen der Vorlesung [[ST WS2020|Sensortechnik]] des Studienschwerpunktes SDE im Studiengang Mechatronik an der Hochschule Hamm-Lippstadt entstanden. Gegenstand des Artikels ist der unipolare Halleffektsensor TLE4905L der Firma Infineon aus Neubiberg. | |||
== Technische Daten== | |||
===Pinbelegung=== | |||
Der TLE4905L hat drei Anschlüsse, bei der Draufsicht (vergleiche Bild oben) ergibt sich folgende Pinbelegung (Datenblatt S.2<ref name = 'Datenblatt'> Infineon: ''Uni- and Bipolar Hall IC Switches for Magnetic Field Applications''. 2007. Online im Internet: https://cdn-reichelt.de/documents/datenblatt/B400/TLE49X5L.pdf Abruf: 13.12.2020</ref>): | |||
{| class="mw-datatable" | |||
! style="font-weight: bold;" | Pin | |||
! style="font-weight: bold;" | Belegung | |||
|- | |||
| 1 | |||
| Versorgungsspannung | |||
|- | |||
| 2 | |||
| Masse | |||
|- | |||
|3 | |||
|Ausgang | |||
|} | |||
===Betriebsparameter=== | |||
{| class="mw-datatable" | |||
! style="font-weight: bold;" | Parameter | |||
! style="font-weight: bold;" | Minimum | |||
! style="font-weight: bold;" | Maximum | |||
|- | |||
| Versorgungsspannung | |||
| 3.8V | |||
|24V | |||
|- | |||
| Betriebstemperatur | |||
| -40°C | |||
|170°C | |||
|- | |||
| Ausgangsstrom | |||
| | |||
|100mA | |||
|- | |||
|Schaltzeit | |||
| | |||
|1µs | |||
|} | |||
===Gehäuseform=== | |||
Der Sensor wird mittels eins PG-SSO-3-2 gehäust. Dabei handelt es sich um ein THT-Gehäuse, welches wie zuvor beschrieben, drei Anschlüsse besitzt. Das Gehäuse ist 4,16 mm breit, 3,29 mm hoch und 1,52 mm dick und besteht aus Kunststoff. Die Anschlüsse haben einen für THT-Typischen Abstand von 1,27 mm (1/20 Zoll).<ref name = 'Datenblatt'/> | |||
== Auswahl eines Primärsensors == | == Auswahl eines Primärsensors == | ||
Wie funktioniert der Sensor? | <!-- Wie funktioniert der Sensor? | ||
Welche Rohsignale liefert der Sensor? | Welche Rohsignale liefert der Sensor? --> | ||
Der Primärsensor des TLE4905 ist ein Hallelement auf Halbleiterbasis. Mittels dieses Elements kann die Stärke eines Magnetfeldes bestimmt werden. Durch die im Sensor durchgeführte Signalverarbeitung kann mit dem Gesamten Sensor bestimmt werden, ob sich dieser in einem Magnetfeld befindet oder nicht. Fall sich der Sensor in einem Magnetfeld mit ausreichender Stärke befindet, kann ein Strom in den Pin 3 (Ausgang) fließen. Ist kein Magnetfeld vorhanden oder ist dieses zu schwach, so kann kein Strom fließen. | |||
===Der Halleffekt=== | |||
[[Datei:Halleffekt.PNG|512px|thumb|rechts|Darstellung des Halleffekts <ref name = 'Thuselt' />, (In der folgenden Herleitung ist "a" mit "d" und "b" mit "h" gleichzusetzen)]] | |||
Der Halleffekt wurde 1879 von [https://de.wikipedia.org/wiki/Edwin_Hall Edwin Herbert Hall] entdeckt, und beschreibt die Spannung in einem Stromdurchflossenen Leiter, der sich in einem Magnetfeld befindet.<ref name = Thuselt>Thuselt, F: ''Physik der Halbleiterbauelemente - Einführendes Lehrbuch für Ingenieure und Physiker''. Berlin: Springer, 3. Auflage 2018. ISBN 978-3-662-57637-3. S.79ff</ref> Diese Spannung tritt im rechten Winkel zum magnetischen Feld und zum Strom, welcher durch den Leiter fließt, auf. Die Grundlage des Effektes ist die Lorenzkraft welche die sich im Leiter und im Magnetfeld bewegenden Ladungsträger ablenkt. Durch diese Ablenkung entsteht auf der einen Seite des Leiters eine höhere Konzentration an Ladungsträgern als auf der gegenüberliegenden. Daraus entsteht eine Spannung zwischen den beiden Seiten des Leiters, die sogenannte Hallspannung. | |||
===Herleitung der Hallspannung=== | |||
Die durch den Halleffekt hervorgerufene Hallspannung basiert auf dem Kräftegleichgewicht aus der Lorenzkraft und des durch die Ablenkung der Ladungsträger hervorgehobenen elektrischen Felds.<ref name = Sauer>Sauer, R: ''Halbleiterphysik Lehrbuch für Physiker und Ingenieure''. München: Oldenbourg Verlag, 2008. ISBN 978-3-486-58863-7. S.23ff</ref> Hierbei erhöht sich die durch die Lorenzkraft resultierende Ladungsverschiebung solange, bis die Kraft des elektrischen Feldes einer weiteren Ladungsverschiebung entgegenwirkt, da sich die beiden Kräfte gegenseitig aufheben. | |||
Im folgenden bezeichnet <math display="inline"> \vec{I} </math> den Strom durch den Leiter sowie <math> \vec{v} </math> die daraus resultierende Driftgeschwindigkeit der Ladungsträger. Das Magnetfeld wird mit <math display="inline"> \vec{B} </math>, das Elektrische Feld mit <math display="inline"> \vec{E} </math>, die Lorenzkraft druch <math display="inline"> \vec{F_L} </math> und die Kraft durch das Elektrische Feld mit <math> \vec{F_E} </math> bezeichnet. Die Elementarladung wird mit <math display="inline"> e </math> bezeichnet. Daraus ergeben sich die folgenden Formeln: | |||
:<math> \vec{F_L} = e \cdot \vec{v} \times \vec{B} </math> | |||
:<math> \vec{F_E} = e \cdot \vec{E} </math> | |||
Aus dem beschriebenen Kräftegleichgewicht folgen dann die folgenden Formeln: | |||
:<math>\begin{align} && \vec{F_L} &= \vec{F_E} \\ | |||
\Leftrightarrow~ && e \cdot \vec{v} \times \vec{B} &= e \cdot \vec{E} \\ | |||
\Leftrightarrow~ && \vec{v} \times \vec{B} &= \vec{E} \\ | |||
\Leftrightarrow~ && \vec{v} \times \vec{B} &= \vec{ \left( \frac{U_H} d \right)} | |||
\end{align}</math> | |||
Hierbei bezeichnet <math> U_H </math> die gesuchte Hallspannung und <math> d </math> die Länge, über die diese Spannung abfällt, beispielsweise die Breite des Leiters. Dementsprechend sind <math> \vec{U_H} </math> ein Vektor und <math> d </math> ein Skalar. Daher kann die Formel wie folgt umgeformt werden: | |||
:<math>\begin{align} | |||
\Leftrightarrow && \vec{v} \times \vec{B} &= \vec{ \left( \frac{U_H} d \right)} \\ | |||
\Leftrightarrow && \vec{v} \times \vec{B} &= \vec{U_H} \cdot \frac 1 d \\ | |||
\Leftrightarrow && d \cdot (\vec{v} \times \vec{B}) &= \vec{U_H} | |||
\end{align}</math> | |||
Die für die Formel benötigte Driftgeschwindigkeit kann über die Stromdichte <math> j </math> errechnet werden.<ref name = Smoliner>Smoliner, J: ''Grundlagen der Halbleiterphysik - Was Studierende der Physik und Elektrotechnik wissen sollten''. Berlin: Springer Spektrum, 2.Auflage 2020. ISBN 978-3-662-60653-7. S.177ff</ref> Die Stromdichte kann für Metalle über die Ladungsträgerdichte <math> n </math> berechnet werden, bei Halbleitern hingegen wird die Dotierungskonzentration, welche näherungsweise der Majoritätsladungsträgerkonzentration <math> n </math> oder <math> p </math> entspricht, verwendet. Es entsteht jeweils eine Formel für die Minoritätsladungsträger und die Majoritätsladungsträger. Da in dotierten Halbleitern die Konzentration der Majoritätsladungsträger meist deutlich größer ist, als jene der Minoritätsladungsträger, können letztere meist aufgrund des deutlich geringeren Effektes vernachlässigt werden. | |||
:<math> | |||
\begin{align} | |||
&& \vec{j} = -e \cdot \vec{v} \cdot n &~\lor~ \vec{j} = e \cdot \vec{v} \cdot p \\ | |||
\Leftrightarrow && \vec{v} = \frac{\vec{j}} {-en} &~\lor~ \vec{v} = \frac{\vec{j}} {ep} | |||
\end{align} | |||
</math> | |||
Die Elementartladung und die Ladungsträgerkonzentration werden wie folgt zur materialabhängigen Hallkonstante <math> R_H </math> zusammengefasst:<ref name = Smoliner/> | |||
:<math> R_H = \frac{1} {-en} ~\lor~ R_H = \frac{1} {ep} </math> | |||
Damit kann die Hallspannung wie folgt errechnet werden: | |||
:<math> \begin{align} | |||
&& \vec{U_H} &&= d \cdot (R_H \cdot \vec{j} \times \vec{B}) \\ | |||
\Leftrightarrow && \vec{U_H} &&= d \cdot (R_H \cdot \frac{\vec{I}} {A} \times \vec{B}) | |||
\end{align}</math> | |||
Dabei ist <math> A </math> die senkrecht zum Stromvektor <math> \vec{I} </math> stehende, von diesem durchflossene Fläche. Zudem wurde die Annahmen getroffen, dass die Stromdichte über diese Fläche homogen ist. | |||
Mit der Annahme, dass der Strom und die Strecke, über welche die Hallspannung gemessen wird, senkrecht zueinander stehen und die Fläche <math> A </math> ein Rechteck ist, kann die Formel weiter vereinfacht werden. Dies ist der fall, da hierdurch die Fläche <math> A </math> als Produkt der Breite <math> d </math> und Höhe <math> h </math> berechnet werden kann. Bei Hallsensoren ist diese Annahme durch die Konstruktion gegeben. | |||
:<math> \begin{align} | |||
&& \vec{U_H} &= d \cdot (R_H \cdot \frac{\vec{I}} {d \cdot h} \times \vec{B}) \\ | |||
\Leftrightarrow && \vec{U_H} &= \frac{1} {h} \cdot R_H \cdot \vec{I} \times \vec{B} \\ | |||
\Rightarrow && U_H &= \frac{R_H \cdot I \cdot B_Z} {h} | |||
\end{align}</math> | |||
== Signalvorverarbeitung == | == Signalvorverarbeitung == | ||
Sollen Messwerte oder vorverarbeitete Daten übertragen werden? | <!-- Sollen Messwerte oder vorverarbeitete Daten übertragen werden? | ||
Wie lässt sich eine Vorverarbeitung umsetzen? | Wie lässt sich eine Vorverarbeitung umsetzen? | ||
Wird eine Kennlinie eingesetzt? Wenn ja, wie wird diese kalibriert? | Wird eine Kennlinie eingesetzt? Wenn ja, wie wird diese kalibriert? --> | ||
[[Datei:TLE4905 Singalverarbeitungskette.PNG|512px|thumb|rechts|Signalverarbeitungskette des Infinion TLE4905L <ref name = 'Datenblatt' />]] | |||
Wie im Bild rechts zu sehen, wird die Spannung des Hallelementes nicht direkt auf den Ausgang des Sensors geschaltet. Dies hängt vor allem damit zusammen, dass die erzeugte Hallspannung sehr gering ist, wodurch sie für die meisten Microkontroller und andere Schaltungen nicht zu verwenden ist. Daher wird die Spannung des Elements zunächst mittels einer Verstärkerschaltung auf ein einfacher zu verarbeitendes Level gebracht. Im Anschluss wird die resultierende Spannung mit einem Schmitt-Trigger ausgewertet. Es gibt also zwei diskrete Ausgangswerte, wodurch eine Kennlinie und die zugehörige Kalibrierung nicht eingesetzt wird. | |||
Um größerer Leistungen schalten zu können folgt nach der Auswertung durch den Schmitt-Trigger noch eine Ausgangsstufe. Diese besteht aus einem Bipolartransistor. Hierdurch kann der Strom deutlich verstärkt werden und die Signalverarbeitung durch einen Microcontroller vereinfacht werden. Als Ausgangsgröße ist damit der Strom zu betrachten der in den Pin 3 (Ausgang) fließt. | |||
Damit ist das direkte Anschließen des Sensor an einen Microcontroller nicht möglich. Wird Pin 3 an direkt an den digitalen Eingang des Microcontrollers angeschlossen, so wird dieser bei ausreichendem magnetischem Feld am Sensor zwar auf das Potential der Masse gezogen, herrscht jedoch kein ausreichendes Magnetfeld, so entsteht am Eingang des Microkotrollers ein unbestimmtes Potential. Damit ist eine zusätzliche Verschaltung des Sensors notwendig. Die einfachste Möglichkeit, welche auch vom Hersteller empfohlen wird besteht darin, das Potential am Ausgang den Sensors über einen Wiederstand auf die Versorgungsspannung anzuheben. So kann bei nicht ausreichendem magnetischem Feld eine HIGH-Potential durch den Microkontroller gelesen werden und bei anliegendem magnetischem Feld ein LOW-Potential. | |||
Der eingelesen logische Wert ist dadurch also invertiert zu Existenz eines ausreichenden magnetischen Feldes: Ohne Magnetfeld wird eine "1" gelesen, mit ausreichendem Magnetfeld eine "0". | |||
== Analog-Digital-Umsetzer == | == Analog-Digital-Umsetzer == | ||
Wie werden die analogen Signale umgesetzt? | <!-- Wie werden die analogen Signale umgesetzt? | ||
Welcher ADU kommt zum Einsatz? | Welcher ADU kommt zum Einsatz?--> | ||
Welche Gründe sprechen für diesen ADU? Alternativen? | Die Analog-Digitalwandlung geschieht beim TLE4905L mittels eines Schmitt-Triggers. Ein Schmitt-Trigger ist ein Schwellwertschalter und besitzt eine Schalthysterese. Die Umsetzung erfolgt über die Verschaltung eines Operationsverstärkers mit Widerständen. Dabei wird der Ausgang des Operationsverstärkers auf den nicht invertierten Eingang gelegt, sodass eine Mitkopplung entsteht.<ref> Baumann, P: ''Prüfungsfragen zur Elektronik - Bachelor Ausbildung''. Wiesbaden: Springer, 2. Auflage 2019. ISBN 978-3-658-26570-0. S.183ff</ref> | ||
<!-- Welche Gründe sprechen für diesen ADU? Alternativen? --> | |||
Im vorliegenden Sensor stellt die Verwendung eines Schmitt-Triggers eine einfache Möglichkeit zur Digitalisierung des analogen Wertes da. Die Verwendung ist hier möglich, da nicht die Intensität des Magnetfeldes gemessen werden soll, sondern ob ein Magnetfeld vorhanden ist. Dieser qualitative Nachweis eines Magnetfeldes benötigt im Vergleich zu einer quantitativen Messung nur ein Bit und kann so durch einen Schmitt-Trigger umgesetzt werden. | |||
Weiterhin bietet der Schmitt-Trigger einen großen Vorteil gegenüber einer Auswertung des Wahrheitswertes über eine Logische Schaltung, welche lediglich auf Basis eines Schwellenwertes die Analog-Digitalwandlung. Durch den Schmitt-Trigger kann eine Hysterese eingefügt werden. Das Löschen des logischen Wertes geschieht erst bei geringeren Spannungen als das Setzten. Hierdurch kann ein schwanken des Ausgabewertes verhindert werden, wenn die Stärke des Magnetfeldes nah am Schwellwert liegt. | |||
== Bussystem == | == Bussystem == | ||
Wird ein Bussystem zwischen Sensor und Mikrocontroller eingesetzt? | <!-- Wird ein Bussystem zwischen Sensor und Mikrocontroller eingesetzt? | ||
Wenn ja, wie funktioniert dieses Bussystem? | Wenn ja, wie funktioniert dieses Bussystem? --> | ||
Zur Übertragung der Daten an einen Microcontroller wird kein Bussystem eingesetzt. Der Ausgewertete Wert des Sensors hat einen Informationsgehalt von 1Bit und gibt an, ob das am Elementarsensor vorliegende Magnetfeld eine gewissen Schwellwert überschritten hat oder nach erfolgter Überschreitung ein niedrigerer Schwellwert unterschritten wurde. Vereinfacht gesagt sagt der Rückgabewert des Sensors also aus, ob ein Magnetfeld vorhanden ist. Diese Information kann über den Pegel am Ausgabepin übertragen werden, wenn eine entsprechende Schaltung mit einem Wiederstand gewählt wird. Der jeweilige Wert kann beispielsweise über einen digitalen Eingang eines Microcontrollers eingelesen werden. | |||
== Digitale Signalverarbeitung == | == Digitale Signalverarbeitung == | ||
<!-- | |||
Welche Verarbeitungsschritte sind notwendig? | Welche Verarbeitungsschritte sind notwendig? | ||
Welche Filter werden angewendet? | Welche Filter werden angewendet? | ||
Bestimmen Sie Auflösung, Empfindlichkeit und Messunsicherheit des Sensors. | Bestimmen Sie Auflösung, Empfindlichkeit und Messunsicherheit des Sensors. | ||
--> | |||
Der notwendige Umfang zur digitalen Signalverarbeitung hängt vom Anwendungsfall ab. Im einfachsten fall wird der Halleffektsensor als Schalter verwendet. Hierbei genügt es den Pegel am Ausgangspin des Sensors mit einem digitalem Eingang am Microcontroller zu verbinden. Eine weiteren digitale Signalverarbeitung ist in diesem Fall nicht notwendig, da der eingelesen Wert direkt verwendet werden kann. Auf diese Weise kann der Sensor zum Beispiel als kontaktloser Endschalter verwendet werden. | |||
Mit den TLE4905L können jedoch auch andere Größen gemessen werden. So ist es möglich die Frequenz eines periodisch schwankenden Magnetfeldes zu messen. Diese Messmethode kann ebenfalls angewandt werden, um die Drehzahl einer Welle zu bestimmen. Hierfür kann ein Permanentmagnet derart auf der Welle angebracht werden, dass dieser mit jeder Umdrehung an dem Sensor vorbeigeführt wird und den Sensor auslöst. Alternativ kann der Sensor in einem magnetischen Kreis eingebaut werden, der von einem sich an der Welle befindlichen magnetischem Material geschlossen und geöffnet wird. Besonders wenn mehr als eine Aktivierung des Sensors pro Umdrehung gewünscht ist, stellt diese Variante in der Regel die günstigerer Lösung dar. | |||
Um aus den Rohdaten des Sensors eine Drehzahl zu ermitteln, muss nun die Zeit gemessen werden, welche zwischen zwei Aktivierungen des Sensor liegt. Dies kann mit einer Interrupt-Service-Routine geschehen, welche den Zeitpunkt der letzten Aktivierung von dem der aktuellen Aktivierung abzieht. Für die Zeitbestimmung kann ein Timer eines Microcontrollers verwendet werden, bei einem Arduino ist dies durch die Methoden millis() und micros() deutlich vereinfacht. Diese geben die Zeit seit Beginn des Programms in Millisekunden respektive Microsekunden wieder. So ist bereits die Periodendauer der letzten Drehung bestimmt. Um hieraus die Drehzahl zu ermitteln, muss der Kehrwert genommen werden und mit einer Konstanten multipliziert werden. Diese Konstante ist, sofern die gewünschte Einheit Umdrehungen pro Minute (U/min) ist und die Periodendauer in Microsekunden gemessen wurde, 60.000.000, da eine Minute ebenso viele Microsekunden umfasst. | |||
:<math> | |||
n = \frac 1 T | |||
</math> | |||
Für den Fall das die zumessende Welle zum Stillstand kommen kann ist des weiteren zu überprüfen, ob die Zeit seit der letzten Aktivierung des Sensors einen Schwellwert überschritten hat. Ist diese beispielsweise größer als 500 ms so kann davon ausgegangen werden, dass die Welle steht. Die Wahl dieses Wertes hängt jedoch vom konkreten Anwendungsfall und dabei von den zu erwartenden Drehzahlen und der gewünschten Reaktionszeit auf eine Stillstand der Welle ab. | |||
== Bewertung der Sensordaten == | == Bewertung der Sensordaten == | ||
Welche Fehler treten in welchem Verarbeitungsschritt auf? | <!--Welche Fehler treten in welchem Verarbeitungsschritt auf? | ||
Stellen Sie die Messunsicherheit bzw. das Vertrauensintervall dar. | Stellen Sie die Messunsicherheit bzw. das Vertrauensintervall dar.--> | ||
Zur Messung der Stärke eines Magnetfeldes ist der TLE4905L denkbar ungeeignet. Dies ist auf zwei Eigenschaften des Sensors zurückzuführen: Zum Einen besitzt der Sensor eine starke Streuung hinsichtlich des erforderlichen magnetischen Feldes zur Aktivierung beziehungsweise Deaktivierung des Schmitt-Triggers.<ref name = 'Datenblatt'/> Das führt dazu, dass die Rohdaten des Sensor zunächst kalibriert werden müssten, um eine Aussage über die Stärke des Magnetischen Feldes treffen zu können. Zum Anderen sind diese Werte zusätzlich noch abhängig von der Temperatur.<ref name = 'Datenblatt'/> Für eine derartigen Einsatz währe also zusätzlich eine Temperaturkompensation notwendig. Da der Sensor jedoch nur eine Schwellwertüberschreitung messen kann, ist dieser Anwendungsfall jedoch ohnehin fraglich. | |||
Wird der Sensor allerdings wie oben beschrieben zur Drehzahlermittlung verwendet, können diese Ungenauigkeiten vernachlässigt werden solange sichergestellt werden kann, dass der Sensor bei jeder Umdrehung zuverlässig auslöst. Bei den ausgewerteten Sensordaten treten dann drei Fehler auf: Erstens wir lediglich die Durchschnittsgeschwindigkeit der letzten Umdrehung gemessen. Änderungen der Drehzahl währen einer Umdrehung können nicht erkannt werden. Dies könnte durch die Verwendung mehrere gleichmäßig verteilter Magneten verbessert werden, oder durch häufigeres Öffnen und Schließen des magnetischen Kreises pro Umdrehung. Ist die Drehzahl jedoch groß genug, so ist die Information in den meisten Anwendungsfällen jedoch ohnehin irrelevant. Zweitens tritt ein Quantisierungsfehler auf, da die Periodendauer nicht kontinuierlich gemessen werden kann. Wird die Zeit in Microsekunden gemessen, so kann jede Drehzahl exakt bestimmt werden, welche durch die folgende Formel bestimmt dargestellt werden kann. | |||
:<math> | |||
n = \frac {60.000.000} {m} \frac {U} {min}, m \in\N, m \geq 2 | |||
</math> | |||
Je größer die Drehzahl wird, desto größer wird auch der Fehler durch die Quantisierung. Je nach akzeptiertem Fehler ergibt sich damit die obere Grenze des Messbereichs. Hierbei ist zusätzlich noch die Schaltdauer des Sensors von 1µs zu beachten. Da der Sensor pro Umdrehung jeweils einmal ein-, und ausschalten muss, können nur Periodendauer von mehr als 2µs gemessen werden. Dies ändert sich auch mit einem schnelleren Microcontroller nicht. Daher ist die maximal messbare Drehzahl durch den Sensor auf 30.000.000 U/min beschränkt, falls nur ein Magnet oder nur eine Unterbrechung des Magnetischen Kreise pro Umlauf verwendet wird. Der dritte Fehler der entstehen kann beruht auf der Erkennung des Stillstandes der Welle. Die Reaktionszeit welche gewählt wird bestimmt ebenfalls die minimale Drehzahl, welche gemessen werden kann. Werden wie oben beschreiben 500 ms verwendet, so können Drehzahlen unterhalb von 120 U/min nicht erkannt werden und werden als 0 U/min gewertet. Dieser Fehler kann ebenfalls verringert werden, wenn mehrerer Magneten oder Unterbrechungen des magnetischen Kreises pro Umlauf verwendet werden. | |||
Neben diesen von der Messmethode abhängigen Fehler kann auch durch die Zeitmessung ein Fehler entstehen. Die Genauigkeit der Zeitmessung wird beim Arduino maßgeblich durch den verbauten Quarz beeinflusst. | |||
== Inbetriebnahme == | == Inbetriebnahme == | ||
Für die Inbetriebnahme wurden zwei Versuche gewählt, die auf dem TLE4905L basieren. Zum einen wurde die Frequenz eines sich ändernden magnetischen Feldes gemessen, zum anderen wurde die Drehzahl einer Standbohrmaschine ermittelt. | |||
[[Datei:Versuchschaltaufbau Hallsensor.jpg|512px|thumb|rechts|Schaltungsaufbau auf einem Steckbrett]] | |||
Für die Schaltung des Sensors wurde dieser mit der Versorgungsspannung eines Arduinos (5V) und dessen Masse verbunden. Der Ausgang des Sensor wurde mit einen interruptfähigen Pin des Arduinos verbunden und über einen 10 kΩ Wiederstand mit der Versorgungsspannung verbunden. Die Ausgabe der ermittelten Drehzahl, beziehungsweise Frequenz geschieht über ein Display welches über den I2C-Bus des Arduinos verbunden wurde. Diese Hardware ist bei beiden Versuchen identisch. | |||
Die Software für die Drehzahlermittlung entspricht der oben beschriebenen Logik, die der Frequenzermittlung ist äquivalent, jedoch mit einer anderen Konstante, da die gewünschte Einheit Hz ist. | |||
Um ein sich änderndes magnetisches Feld zu erzeugen, wurde eine Spule mit Eisenkern über eine Transformator an das Stromnetz angeschlossen. Für die Spule wurde eine verzinkte Eisenschraube mit einem isoliertem Draht umwickelt. Die Einsenschraube wurde verwendet, um durch das vergleichsweise hohe <math>\mu_r</math> einen stärkeren Elektromagneten herzustellen. Die Spule wurde mit eine Wechselspannung von 50 Hz, einem Effektivwert der Spannung von 0,62 V und versorgt, so dass sich ein Storm von 5 A einstellt (ebenfalls Effektivwert). Diese Spule wurde mit dem enthaltenen Eisenkern vor den Halleffektsensor gehalten, sodass dieser von dem Magnetfeld durchflossen wurde. Es wurde eine Frequenz von 50,0 Hz durch die Auswertung gemessen. | |||
Für den zweiten Versuch wurde ein Permanentmagnet an einem 10 mm Metallbohrer befestigt, welche im Anschluss in eine Standbohrmaschine mit variabler Drehzahl eingespannt wurde. Der Hallsensor wurde in der Nähe des Magneten platziert. Während der Versuchsdurchführung wurde die Drehzahl der Maschine zunächst von ca. 500 U/min bis 900 U/min und in einem zweiten Durchlauf von ca. 1000 U/min bis 2200 U/min variiert. Die Drehzahl konnte hierbei zuverlässig ermittelt werden. | |||
''' Frequenzmessung: ''' | |||
<gallery widths="250" heights="250"> | |||
Datei:Hallsensor Spule.jpg|Spule mit 42 Windungen | |||
Datei:Hallsensor Spule Strom.jpg|Strom druch die Spule | |||
Datei:Hallsensor Spule Spannung.jpg|Spannung an der Spule | |||
Datei:Hallsensor Spule Frequenz.jpg|Frequenz des Wechselstroms | |||
</gallery> | |||
''' Drehzahlmessung: ''' | |||
<gallery widths="250" heights="250"> | |||
Datei:Hallsensor Drehzahl 0.jpg|Drehzahlmessung bei Stillstand | |||
Datei:Hallsensor Drehzahl 502.jpg|Drehzahlmessung bei einer Drehzahl von 502 U/min | |||
</gallery> | |||
=== YouTube-Video === | === YouTube-Video === | ||
In diesem [https://www.youtube.com/embed/XNLgrx6Xb18/ Video] ist die Inbetriebnahme zu sehen. | |||
== Literatur == | == Literatur == | ||
<references /> | <references /> | ||
---- | ---- | ||
→ zurück zum Hauptartikel: [[ST WS2020|Sensortechnik WS 20/21]] | → zurück zum Hauptartikel: [[ST WS2020|Sensortechnik WS 20/21]] | ||
Aktuelle Version vom 12. Januar 2021, 12:55 Uhr

Autor: Mario Wollschläger
Betreuer: Prof. Dr.-Ing. Ulrich Schneider
Einleitung
Dieser Artikel ist im Rahmen der Vorlesung Sensortechnik des Studienschwerpunktes SDE im Studiengang Mechatronik an der Hochschule Hamm-Lippstadt entstanden. Gegenstand des Artikels ist der unipolare Halleffektsensor TLE4905L der Firma Infineon aus Neubiberg.
Technische Daten
Pinbelegung
Der TLE4905L hat drei Anschlüsse, bei der Draufsicht (vergleiche Bild oben) ergibt sich folgende Pinbelegung (Datenblatt S.2[2]):
| Pin | Belegung |
|---|---|
| 1 | Versorgungsspannung |
| 2 | Masse |
| 3 | Ausgang |
Betriebsparameter
| Parameter | Minimum | Maximum |
|---|---|---|
| Versorgungsspannung | 3.8V | 24V |
| Betriebstemperatur | -40°C | 170°C |
| Ausgangsstrom | 100mA | |
| Schaltzeit | 1µs |
Gehäuseform
Der Sensor wird mittels eins PG-SSO-3-2 gehäust. Dabei handelt es sich um ein THT-Gehäuse, welches wie zuvor beschrieben, drei Anschlüsse besitzt. Das Gehäuse ist 4,16 mm breit, 3,29 mm hoch und 1,52 mm dick und besteht aus Kunststoff. Die Anschlüsse haben einen für THT-Typischen Abstand von 1,27 mm (1/20 Zoll).[2]
Auswahl eines Primärsensors
Der Primärsensor des TLE4905 ist ein Hallelement auf Halbleiterbasis. Mittels dieses Elements kann die Stärke eines Magnetfeldes bestimmt werden. Durch die im Sensor durchgeführte Signalverarbeitung kann mit dem Gesamten Sensor bestimmt werden, ob sich dieser in einem Magnetfeld befindet oder nicht. Fall sich der Sensor in einem Magnetfeld mit ausreichender Stärke befindet, kann ein Strom in den Pin 3 (Ausgang) fließen. Ist kein Magnetfeld vorhanden oder ist dieses zu schwach, so kann kein Strom fließen.
Der Halleffekt
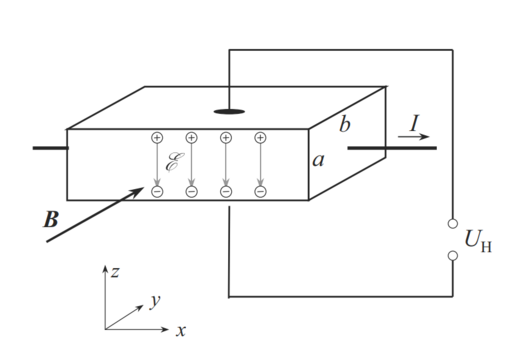
Der Halleffekt wurde 1879 von Edwin Herbert Hall entdeckt, und beschreibt die Spannung in einem Stromdurchflossenen Leiter, der sich in einem Magnetfeld befindet.[3] Diese Spannung tritt im rechten Winkel zum magnetischen Feld und zum Strom, welcher durch den Leiter fließt, auf. Die Grundlage des Effektes ist die Lorenzkraft welche die sich im Leiter und im Magnetfeld bewegenden Ladungsträger ablenkt. Durch diese Ablenkung entsteht auf der einen Seite des Leiters eine höhere Konzentration an Ladungsträgern als auf der gegenüberliegenden. Daraus entsteht eine Spannung zwischen den beiden Seiten des Leiters, die sogenannte Hallspannung.
Herleitung der Hallspannung
Die durch den Halleffekt hervorgerufene Hallspannung basiert auf dem Kräftegleichgewicht aus der Lorenzkraft und des durch die Ablenkung der Ladungsträger hervorgehobenen elektrischen Felds.[4] Hierbei erhöht sich die durch die Lorenzkraft resultierende Ladungsverschiebung solange, bis die Kraft des elektrischen Feldes einer weiteren Ladungsverschiebung entgegenwirkt, da sich die beiden Kräfte gegenseitig aufheben.
Im folgenden bezeichnet den Strom durch den Leiter sowie die daraus resultierende Driftgeschwindigkeit der Ladungsträger. Das Magnetfeld wird mit , das Elektrische Feld mit , die Lorenzkraft druch und die Kraft durch das Elektrische Feld mit bezeichnet. Die Elementarladung wird mit bezeichnet. Daraus ergeben sich die folgenden Formeln:
Aus dem beschriebenen Kräftegleichgewicht folgen dann die folgenden Formeln:
Hierbei bezeichnet die gesuchte Hallspannung und die Länge, über die diese Spannung abfällt, beispielsweise die Breite des Leiters. Dementsprechend sind ein Vektor und ein Skalar. Daher kann die Formel wie folgt umgeformt werden:
Die für die Formel benötigte Driftgeschwindigkeit kann über die Stromdichte errechnet werden.[5] Die Stromdichte kann für Metalle über die Ladungsträgerdichte berechnet werden, bei Halbleitern hingegen wird die Dotierungskonzentration, welche näherungsweise der Majoritätsladungsträgerkonzentration oder entspricht, verwendet. Es entsteht jeweils eine Formel für die Minoritätsladungsträger und die Majoritätsladungsträger. Da in dotierten Halbleitern die Konzentration der Majoritätsladungsträger meist deutlich größer ist, als jene der Minoritätsladungsträger, können letztere meist aufgrund des deutlich geringeren Effektes vernachlässigt werden.
Die Elementartladung und die Ladungsträgerkonzentration werden wie folgt zur materialabhängigen Hallkonstante zusammengefasst:[5]
Damit kann die Hallspannung wie folgt errechnet werden:
Dabei ist die senkrecht zum Stromvektor stehende, von diesem durchflossene Fläche. Zudem wurde die Annahmen getroffen, dass die Stromdichte über diese Fläche homogen ist.
Mit der Annahme, dass der Strom und die Strecke, über welche die Hallspannung gemessen wird, senkrecht zueinander stehen und die Fläche ein Rechteck ist, kann die Formel weiter vereinfacht werden. Dies ist der fall, da hierdurch die Fläche als Produkt der Breite und Höhe berechnet werden kann. Bei Hallsensoren ist diese Annahme durch die Konstruktion gegeben.
Signalvorverarbeitung
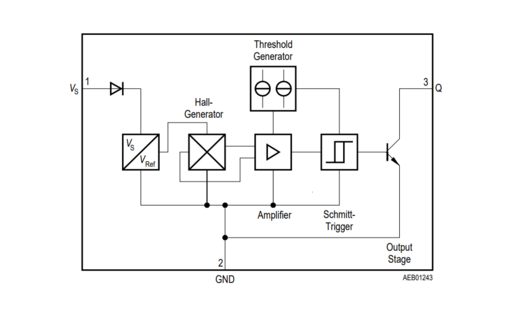
Wie im Bild rechts zu sehen, wird die Spannung des Hallelementes nicht direkt auf den Ausgang des Sensors geschaltet. Dies hängt vor allem damit zusammen, dass die erzeugte Hallspannung sehr gering ist, wodurch sie für die meisten Microkontroller und andere Schaltungen nicht zu verwenden ist. Daher wird die Spannung des Elements zunächst mittels einer Verstärkerschaltung auf ein einfacher zu verarbeitendes Level gebracht. Im Anschluss wird die resultierende Spannung mit einem Schmitt-Trigger ausgewertet. Es gibt also zwei diskrete Ausgangswerte, wodurch eine Kennlinie und die zugehörige Kalibrierung nicht eingesetzt wird.
Um größerer Leistungen schalten zu können folgt nach der Auswertung durch den Schmitt-Trigger noch eine Ausgangsstufe. Diese besteht aus einem Bipolartransistor. Hierdurch kann der Strom deutlich verstärkt werden und die Signalverarbeitung durch einen Microcontroller vereinfacht werden. Als Ausgangsgröße ist damit der Strom zu betrachten der in den Pin 3 (Ausgang) fließt.
Damit ist das direkte Anschließen des Sensor an einen Microcontroller nicht möglich. Wird Pin 3 an direkt an den digitalen Eingang des Microcontrollers angeschlossen, so wird dieser bei ausreichendem magnetischem Feld am Sensor zwar auf das Potential der Masse gezogen, herrscht jedoch kein ausreichendes Magnetfeld, so entsteht am Eingang des Microkotrollers ein unbestimmtes Potential. Damit ist eine zusätzliche Verschaltung des Sensors notwendig. Die einfachste Möglichkeit, welche auch vom Hersteller empfohlen wird besteht darin, das Potential am Ausgang den Sensors über einen Wiederstand auf die Versorgungsspannung anzuheben. So kann bei nicht ausreichendem magnetischem Feld eine HIGH-Potential durch den Microkontroller gelesen werden und bei anliegendem magnetischem Feld ein LOW-Potential.
Der eingelesen logische Wert ist dadurch also invertiert zu Existenz eines ausreichenden magnetischen Feldes: Ohne Magnetfeld wird eine "1" gelesen, mit ausreichendem Magnetfeld eine "0".
Analog-Digital-Umsetzer
Die Analog-Digitalwandlung geschieht beim TLE4905L mittels eines Schmitt-Triggers. Ein Schmitt-Trigger ist ein Schwellwertschalter und besitzt eine Schalthysterese. Die Umsetzung erfolgt über die Verschaltung eines Operationsverstärkers mit Widerständen. Dabei wird der Ausgang des Operationsverstärkers auf den nicht invertierten Eingang gelegt, sodass eine Mitkopplung entsteht.[6]
Im vorliegenden Sensor stellt die Verwendung eines Schmitt-Triggers eine einfache Möglichkeit zur Digitalisierung des analogen Wertes da. Die Verwendung ist hier möglich, da nicht die Intensität des Magnetfeldes gemessen werden soll, sondern ob ein Magnetfeld vorhanden ist. Dieser qualitative Nachweis eines Magnetfeldes benötigt im Vergleich zu einer quantitativen Messung nur ein Bit und kann so durch einen Schmitt-Trigger umgesetzt werden.
Weiterhin bietet der Schmitt-Trigger einen großen Vorteil gegenüber einer Auswertung des Wahrheitswertes über eine Logische Schaltung, welche lediglich auf Basis eines Schwellenwertes die Analog-Digitalwandlung. Durch den Schmitt-Trigger kann eine Hysterese eingefügt werden. Das Löschen des logischen Wertes geschieht erst bei geringeren Spannungen als das Setzten. Hierdurch kann ein schwanken des Ausgabewertes verhindert werden, wenn die Stärke des Magnetfeldes nah am Schwellwert liegt.
Bussystem
Zur Übertragung der Daten an einen Microcontroller wird kein Bussystem eingesetzt. Der Ausgewertete Wert des Sensors hat einen Informationsgehalt von 1Bit und gibt an, ob das am Elementarsensor vorliegende Magnetfeld eine gewissen Schwellwert überschritten hat oder nach erfolgter Überschreitung ein niedrigerer Schwellwert unterschritten wurde. Vereinfacht gesagt sagt der Rückgabewert des Sensors also aus, ob ein Magnetfeld vorhanden ist. Diese Information kann über den Pegel am Ausgabepin übertragen werden, wenn eine entsprechende Schaltung mit einem Wiederstand gewählt wird. Der jeweilige Wert kann beispielsweise über einen digitalen Eingang eines Microcontrollers eingelesen werden.
Digitale Signalverarbeitung
Der notwendige Umfang zur digitalen Signalverarbeitung hängt vom Anwendungsfall ab. Im einfachsten fall wird der Halleffektsensor als Schalter verwendet. Hierbei genügt es den Pegel am Ausgangspin des Sensors mit einem digitalem Eingang am Microcontroller zu verbinden. Eine weiteren digitale Signalverarbeitung ist in diesem Fall nicht notwendig, da der eingelesen Wert direkt verwendet werden kann. Auf diese Weise kann der Sensor zum Beispiel als kontaktloser Endschalter verwendet werden.
Mit den TLE4905L können jedoch auch andere Größen gemessen werden. So ist es möglich die Frequenz eines periodisch schwankenden Magnetfeldes zu messen. Diese Messmethode kann ebenfalls angewandt werden, um die Drehzahl einer Welle zu bestimmen. Hierfür kann ein Permanentmagnet derart auf der Welle angebracht werden, dass dieser mit jeder Umdrehung an dem Sensor vorbeigeführt wird und den Sensor auslöst. Alternativ kann der Sensor in einem magnetischen Kreis eingebaut werden, der von einem sich an der Welle befindlichen magnetischem Material geschlossen und geöffnet wird. Besonders wenn mehr als eine Aktivierung des Sensors pro Umdrehung gewünscht ist, stellt diese Variante in der Regel die günstigerer Lösung dar.
Um aus den Rohdaten des Sensors eine Drehzahl zu ermitteln, muss nun die Zeit gemessen werden, welche zwischen zwei Aktivierungen des Sensor liegt. Dies kann mit einer Interrupt-Service-Routine geschehen, welche den Zeitpunkt der letzten Aktivierung von dem der aktuellen Aktivierung abzieht. Für die Zeitbestimmung kann ein Timer eines Microcontrollers verwendet werden, bei einem Arduino ist dies durch die Methoden millis() und micros() deutlich vereinfacht. Diese geben die Zeit seit Beginn des Programms in Millisekunden respektive Microsekunden wieder. So ist bereits die Periodendauer der letzten Drehung bestimmt. Um hieraus die Drehzahl zu ermitteln, muss der Kehrwert genommen werden und mit einer Konstanten multipliziert werden. Diese Konstante ist, sofern die gewünschte Einheit Umdrehungen pro Minute (U/min) ist und die Periodendauer in Microsekunden gemessen wurde, 60.000.000, da eine Minute ebenso viele Microsekunden umfasst.
Für den Fall das die zumessende Welle zum Stillstand kommen kann ist des weiteren zu überprüfen, ob die Zeit seit der letzten Aktivierung des Sensors einen Schwellwert überschritten hat. Ist diese beispielsweise größer als 500 ms so kann davon ausgegangen werden, dass die Welle steht. Die Wahl dieses Wertes hängt jedoch vom konkreten Anwendungsfall und dabei von den zu erwartenden Drehzahlen und der gewünschten Reaktionszeit auf eine Stillstand der Welle ab.
Bewertung der Sensordaten
Zur Messung der Stärke eines Magnetfeldes ist der TLE4905L denkbar ungeeignet. Dies ist auf zwei Eigenschaften des Sensors zurückzuführen: Zum Einen besitzt der Sensor eine starke Streuung hinsichtlich des erforderlichen magnetischen Feldes zur Aktivierung beziehungsweise Deaktivierung des Schmitt-Triggers.[2] Das führt dazu, dass die Rohdaten des Sensor zunächst kalibriert werden müssten, um eine Aussage über die Stärke des Magnetischen Feldes treffen zu können. Zum Anderen sind diese Werte zusätzlich noch abhängig von der Temperatur.[2] Für eine derartigen Einsatz währe also zusätzlich eine Temperaturkompensation notwendig. Da der Sensor jedoch nur eine Schwellwertüberschreitung messen kann, ist dieser Anwendungsfall jedoch ohnehin fraglich.
Wird der Sensor allerdings wie oben beschrieben zur Drehzahlermittlung verwendet, können diese Ungenauigkeiten vernachlässigt werden solange sichergestellt werden kann, dass der Sensor bei jeder Umdrehung zuverlässig auslöst. Bei den ausgewerteten Sensordaten treten dann drei Fehler auf: Erstens wir lediglich die Durchschnittsgeschwindigkeit der letzten Umdrehung gemessen. Änderungen der Drehzahl währen einer Umdrehung können nicht erkannt werden. Dies könnte durch die Verwendung mehrere gleichmäßig verteilter Magneten verbessert werden, oder durch häufigeres Öffnen und Schließen des magnetischen Kreises pro Umdrehung. Ist die Drehzahl jedoch groß genug, so ist die Information in den meisten Anwendungsfällen jedoch ohnehin irrelevant. Zweitens tritt ein Quantisierungsfehler auf, da die Periodendauer nicht kontinuierlich gemessen werden kann. Wird die Zeit in Microsekunden gemessen, so kann jede Drehzahl exakt bestimmt werden, welche durch die folgende Formel bestimmt dargestellt werden kann.
Je größer die Drehzahl wird, desto größer wird auch der Fehler durch die Quantisierung. Je nach akzeptiertem Fehler ergibt sich damit die obere Grenze des Messbereichs. Hierbei ist zusätzlich noch die Schaltdauer des Sensors von 1µs zu beachten. Da der Sensor pro Umdrehung jeweils einmal ein-, und ausschalten muss, können nur Periodendauer von mehr als 2µs gemessen werden. Dies ändert sich auch mit einem schnelleren Microcontroller nicht. Daher ist die maximal messbare Drehzahl durch den Sensor auf 30.000.000 U/min beschränkt, falls nur ein Magnet oder nur eine Unterbrechung des Magnetischen Kreise pro Umlauf verwendet wird. Der dritte Fehler der entstehen kann beruht auf der Erkennung des Stillstandes der Welle. Die Reaktionszeit welche gewählt wird bestimmt ebenfalls die minimale Drehzahl, welche gemessen werden kann. Werden wie oben beschreiben 500 ms verwendet, so können Drehzahlen unterhalb von 120 U/min nicht erkannt werden und werden als 0 U/min gewertet. Dieser Fehler kann ebenfalls verringert werden, wenn mehrerer Magneten oder Unterbrechungen des magnetischen Kreises pro Umlauf verwendet werden.
Neben diesen von der Messmethode abhängigen Fehler kann auch durch die Zeitmessung ein Fehler entstehen. Die Genauigkeit der Zeitmessung wird beim Arduino maßgeblich durch den verbauten Quarz beeinflusst.
Inbetriebnahme
Für die Inbetriebnahme wurden zwei Versuche gewählt, die auf dem TLE4905L basieren. Zum einen wurde die Frequenz eines sich ändernden magnetischen Feldes gemessen, zum anderen wurde die Drehzahl einer Standbohrmaschine ermittelt.

Für die Schaltung des Sensors wurde dieser mit der Versorgungsspannung eines Arduinos (5V) und dessen Masse verbunden. Der Ausgang des Sensor wurde mit einen interruptfähigen Pin des Arduinos verbunden und über einen 10 kΩ Wiederstand mit der Versorgungsspannung verbunden. Die Ausgabe der ermittelten Drehzahl, beziehungsweise Frequenz geschieht über ein Display welches über den I2C-Bus des Arduinos verbunden wurde. Diese Hardware ist bei beiden Versuchen identisch.
Die Software für die Drehzahlermittlung entspricht der oben beschriebenen Logik, die der Frequenzermittlung ist äquivalent, jedoch mit einer anderen Konstante, da die gewünschte Einheit Hz ist.
Um ein sich änderndes magnetisches Feld zu erzeugen, wurde eine Spule mit Eisenkern über eine Transformator an das Stromnetz angeschlossen. Für die Spule wurde eine verzinkte Eisenschraube mit einem isoliertem Draht umwickelt. Die Einsenschraube wurde verwendet, um durch das vergleichsweise hohe einen stärkeren Elektromagneten herzustellen. Die Spule wurde mit eine Wechselspannung von 50 Hz, einem Effektivwert der Spannung von 0,62 V und versorgt, so dass sich ein Storm von 5 A einstellt (ebenfalls Effektivwert). Diese Spule wurde mit dem enthaltenen Eisenkern vor den Halleffektsensor gehalten, sodass dieser von dem Magnetfeld durchflossen wurde. Es wurde eine Frequenz von 50,0 Hz durch die Auswertung gemessen.
Für den zweiten Versuch wurde ein Permanentmagnet an einem 10 mm Metallbohrer befestigt, welche im Anschluss in eine Standbohrmaschine mit variabler Drehzahl eingespannt wurde. Der Hallsensor wurde in der Nähe des Magneten platziert. Während der Versuchsdurchführung wurde die Drehzahl der Maschine zunächst von ca. 500 U/min bis 900 U/min und in einem zweiten Durchlauf von ca. 1000 U/min bis 2200 U/min variiert. Die Drehzahl konnte hierbei zuverlässig ermittelt werden.
Frequenzmessung:
-
Spule mit 42 Windungen
-
Strom druch die Spule
-
Spannung an der Spule
-
Frequenz des Wechselstroms
Drehzahlmessung:
-
Drehzahlmessung bei Stillstand
-
Drehzahlmessung bei einer Drehzahl von 502 U/min
YouTube-Video
In diesem Video ist die Inbetriebnahme zu sehen.
Literatur
- ↑ https://cdn-reichelt.de/bilder/web/artikel_ws/B400/PICTURE_2SS52M.jpg
- ↑ 2,0 2,1 2,2 2,3 2,4 Infineon: Uni- and Bipolar Hall IC Switches for Magnetic Field Applications. 2007. Online im Internet: https://cdn-reichelt.de/documents/datenblatt/B400/TLE49X5L.pdf Abruf: 13.12.2020
- ↑ 3,0 3,1 Thuselt, F: Physik der Halbleiterbauelemente - Einführendes Lehrbuch für Ingenieure und Physiker. Berlin: Springer, 3. Auflage 2018. ISBN 978-3-662-57637-3. S.79ff
- ↑ Sauer, R: Halbleiterphysik Lehrbuch für Physiker und Ingenieure. München: Oldenbourg Verlag, 2008. ISBN 978-3-486-58863-7. S.23ff
- ↑ 5,0 5,1 Smoliner, J: Grundlagen der Halbleiterphysik - Was Studierende der Physik und Elektrotechnik wissen sollten. Berlin: Springer Spektrum, 2.Auflage 2020. ISBN 978-3-662-60653-7. S.177ff
- ↑ Baumann, P: Prüfungsfragen zur Elektronik - Bachelor Ausbildung. Wiesbaden: Springer, 2. Auflage 2019. ISBN 978-3-658-26570-0. S.183ff
→ zurück zum Hauptartikel: Sensortechnik WS 20/21





